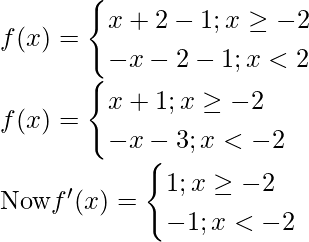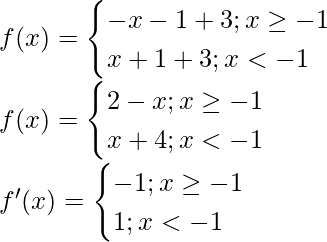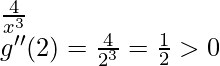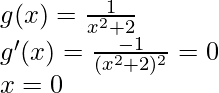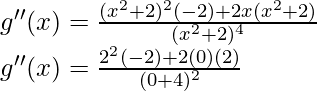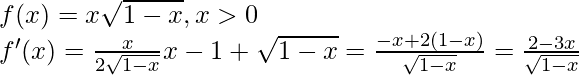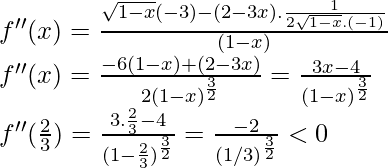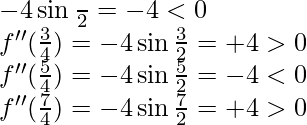Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.5

Pregunta 1. Encuentra los valores máximo y mínimo, si los hay, de la siguiente función dada por

(yo) f(x) = (2x – 1) ² + 3

Solución:

Dado que, f(x) = (2x – 1) ² + 3

De la función dada observamos que

(2x – 1) ² ≥ 0 ∀ x∈ R,

Asi que,

(2x – 1) ² + 3 ≥ 3 ∀ x∈ R,

Ahora encontramos el valor mínimo de la función f cuando 2x-1 = 0

Entonces, x = 1/2

f = f(1/2) = (2(1/2) – 1) ² + 3 = 3

Por lo tanto, el valor mínimo de la función es 3 y esta función no contiene el valor máximo.

(ii) f(x) = 9x ² + 12x + 2

Solución:

Dado que, f(x) = 9x ² + 12x + 2

también podemos escribir como f(x) = (3x + 2) ² – 2

De la función dada observamos que

(3x + 2) ² ≥ 0 ∀ x∈ R,

Asi que,

(3x + 2) ² – 2 ≥ 2 ∀ x∈ R,

Ahora encontramos el valor mínimo de la función f cuando 3x + 2 = 0

Entonces, x = -2/3

f = f(-2/3) = (3(-2/3) + 2) ² – 2 = -2

Por lo tanto, el valor mínimo de la función es -2 y esta función no contiene el valor máximo.

(iii) f(x) = -(x – 1) ² + 10

Solución:

Dado que, f(x) = -(x – 1) ² + 10

De la función dada observamos que

(x – 1) ² ≥ 0 ∀ x∈ R,

Asi que,

-(x – 1) ² + 10 ≤ 10 ∀ x∈ R,

Ahora encontramos el valor máximo de la función f cuando x – 1 = 0

Entonces, x = 1

f = f(1) = -(1 – 1) ² +10 = 10

Por lo tanto, el valor máximo de la función es 10 y esta función no contiene valor mínimo.

(iv) g(x) = x3 ⁺ 1

Solución:

Dado que, g(x) = x ³ + 1

Cuando x —> ∞, entonces g(x) —> ∞

Cuando x —> -∞, entonces g(x) —> -∞

Entonces, esta función no tiene valor mínimo ni máximo.

Pregunta 2. Encuentra los valores máximo y mínimo, si los hay, de las siguientes funciones dadas por

(yo) f(x) = |x + 2| – 1

Solución:

Dado que, f(x) = |x + 2| – 1

$f(x)= \begin{cases} x+2-1; x\ge -2 \\ -x-2-1; x<2 \end{cases} \\ f(x)= \begin{cases} x+1;x\ge -2\\ -x-3;x<-2 \end{cases}\\ \text{Now}\space f'(x)=\begin{cases} 1;x\ge -2\\ -1;x<-2 \end{cases}$

En x = -2 f'(x) cambia el signo de negativo a positivo, por lo tanto, mediante la prueba de la primera derivada, x = -2

es un punto de mínimos locales.

Entonces, el valor mínimo f = f(-1)= |(-1)+ 2| – 1 = -1

Entonces esta función no contiene el valor máximo.

(ii) g(x) = -|x + 1| + 3

Solución:

Dado que, g(x) = -|x + 1| + 3

$f(x)= \begin{cases} -x-1+3; x\ge -1 \\ x+1+3; x<-1 \end{cases} \\ f(x)= \begin{cases} 2-x;x\ge -1\\ x+4;x<-1 \end{cases}\\ f'(x)=\begin{cases} -1;x\ge -1\\ 1;x<-1 \end{cases}$

En x = -1 f'(x) cambia el signo de positivo a negativo, por lo tanto, mediante la prueba de la primera derivada, x = -1

es un punto de mínimos locales.

Entonces, el valor máximo de f = f(-1) = -|(-1) + 1| + 3 = 3

Entonces, esta función no contiene un valor mínimo.

(iii) h(x) = sen 2x + 5

Solución:

Dado que, h(x) = sen(2x) + 5

Al diferenciar ambos lados de x, obtenemos

h'(x) = 2cos2x

Ahora pon h'(x) = 0

2cos 2x = 0

2x = (2x – 1)π/2

x = (2x – 1)π/4

$x=&pm;π/4,&pm;\frac{3π}{4},&pm;\frac{5π}{4}...$

Realicemos la prueba de la segunda derivada,

h”(x) = -4sen2x

h”(π/4) < 0

$h''(\frac{3π}{4} )>0;h''(\frac{5π}{4})<0$

& pronto.

Asi que, $x=\frac{π}{4},\frac{-3π}{4},\frac{5π}{4}\frac{-7π}{4}\frac{9π}{4}.....\text{are \space points}$

de máximos locales.

& $x=\frac{-π}{4},\frac{3π}{4},\frac{-5π}{4}....$ son puntos de mínimos locales.

Entonces, el valor mínimo de la función dada es 4 y el valor máximo de la función dada es 6

(iv) f(x) = |sin(4x + 3)|

Solución:

Dado que, f(x) = |sin(4x + 3)|

Ahora, para cualquier valor de x, sin4x tiene el valor mínimo como -1. es decir, sen 4x + 3 ≥ 2

Entonces f(x) = |sin(4x + 3)| = sen 4x + 3

Al diferenciar ambos lados de x, obtenemos

f'(x) = 4cos4x

Ahora pon f'(x) = 0

4cos 4x = 0

4x = (2x – 1)π/2

x = (2x – 1)π/8

$x=&pm;\frac{π}{8},&pm;\frac{3π}{8},&pm;\frac{7π}{8}....$ & hijo en

Realicemos la prueba de la segunda derivada,

f”(x) = -16 sen4x

f”(π/8) < 0; f”(3π/8) > 0; f”(5π/8) < 0

Entonces, $x=\frac{π}{8},\frac{-3π}{8},\frac{5π}{8},\frac{-7π}{8}$ …. son puntos de máximos locales. Valor mínimo = 4.

& $x=\frac{-π}{8},\frac{3π}{8},\frac{-5π}{8},\frac{7π}{8}$ son puntos de mínimos locales. Valor mínimo = 2.

(v) h(x) = x + 1, x ∈ (-1, 1)

Solución:

Dado que, h(x) = x + 1, x ∈ (-1, 1)

Como podemos ver claramente a partir de la función, h(x) es una función estrictamente creciente.

Entonces, el valor mínimo de x dará el valor mínimo de h(x).

Ahora, x ∈ (-1, 1)

Por lo tanto, esta función no tiene valor mínimo ni máximo.

Pregunta 3. Encuentra los máximos locales y los mínimos locales, si los hay, de las siguientes funciones. Encuentre también los valores máximo local y mínimo local, según sea el caso:

(yo) f(x) = x ²

Solución:

Dado que f(x) = x ²

Al diferenciar ambos lados de x, obtenemos

f'(x) = 2x

Ahora pon f'(x) = 0

2x = 0

x = 0

Hagamos la prueba de la segunda derivada,

f”(x) = 2 > 0

En, x = 0, f'(x) = 0 y f”(x) > 0,

Entonces x = 0 es un punto de mínimos locales. Valor mínimo local.

(ii) g(x) = x ³ – 3x

Solución:

Dado que g(x) = x ³ – 3x

Al diferenciar ambos lados de x, obtenemos

g'(x) = 3x ² – 3

Ahora pon g'(x) = 0

3x ² – 3 = 0

× ² = 1

x = ±1

Hagamos el criterio de la segunda derivada,

g”(x) = 6x ….(yo)

g”(1) = 6 > 0

g”(-1) = -6 > 0

Entonces, por la prueba de las segundas derivadas, x = 1 es un punto de máximos locales y el valor máximo es

g(1) = (1) ³ – 3(1) = -2

Entonces, por la prueba de las segundas derivadas, x = -1 es un punto de mínimos locales y el valor mínimo es

g(-1) = (-1) ³ – 3(-1) = 2

Por lo tanto, el valor mínimo local es -2 y el valor máximo local es 2

(iii) h(x) = sen x + cos x, 0 < x < π/2

Solución:

h(x) = sen x + cos x, x∈(0,π/2)

Al diferenciar ambos lados de x, obtenemos

h'(x) = cos x – sen x

Ahora pon h'(x) = 0

cos x – sen x = 0

cos x = sen x, x ∈ (0, π/2)

Claramente x = π/4 [tanto cos x como sen x alcanzan 1/√2 en π/4]

Hagamos la prueba de la segunda derivada,

h”(x) = -sen x – cos x

h”(π/4) = $-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}<0$

En $x=\frac{π}{4}$ es un punto de máximos locales y el valor máximo es

h(π/4) = sen π/4 + cos π/4

= 1/√2 + 1/√2 = √2

(iv) f(x) = sen x – cos x, 0 < x < 2π

Solución:

Dado que, f(x) = sen x – cos x, x ∈ (0, 2π)

Al diferenciar ambos lados de x, obtenemos

f'(x) = cos x + sen x

Ahora pon f'(x) = 0

cos x + sen x = 0

x = $\frac{3π}{4},\frac{7π}{4}\space$ en (0, 2π)

Ahora hagamos el criterio de la segunda derivada

f”(x) = -sen x + cos x

f”(3 π /4) = – √2 > 0

f”(7 π /4) = √2 > 0

Entonces, por la prueba de las segundas derivadas, x = $\frac{3π}{4}$ es un punto de máximos locales y el valor máximo es

f( $\frac{3π}{4}$ ) = -sen 3 π /4 + cos 3 π 4
= 1/√2 + 1/√2 = √2 > 0

Entonces, por la prueba de las segundas derivadas, x = $\frac{7π}{4}$ es un punto de mínimos locales y el valor mínimo es

f( $\frac{7π}{4}$ ) = -sen 7 π /4 + cos 7 π 4
= -1/√2 – 1/√2 = -√2 > 0

Por lo tanto, el valor mínimo local es -√2 y el valor máximo local es √2.

(v) f(x) = x ³ – 6x ² + 9x + 15

Solución:

Dado que, f(x) = x ³ – 6x ² + 9x + 15

Al diferenciar ambos lados de x, obtenemos

f'(x) = 3x ² – 12x + 9

Ahora pon f'(x) = 0

3x ² – 12x + 9 = 0

3(x ² – 4x + 3) = 0

x = 1, 3

Hagamos el criterio de la segunda derivada,

f”(x) = 6x – 12

f”(1) = -6 < 0

f”(3) = 6 > 0

Entonces, por la prueba de las segundas derivadas, x = 1 es un punto de máximos locales y el valor máximo es

f'(1) = 3(1) ² – 12(1) + 9 = 19

Entonces, por la prueba de las segundas derivadas, x = 3 es un punto de mínimos locales y el valor mínimo es

f'(3) = 3(3) ² – 12(3) + 9 = 15

Por lo tanto, el valor mínimo local es 15 y el valor máximo local es 19.

(vi) 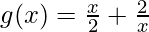$g(x)=\frac{x}{2}+\frac{2}{x}$ , x > 0

Solución:

Dado que, $g(x)=\frac{x}{2}+\frac{2}{x}$ , x > 0

Al diferenciar ambos lados de x, obtenemos

g'(x)= $\frac{1}{2}-\frac{2}{x^2}$

Ahora pon g'(x) = 0

$\frac{1}{2}-\frac{2}{x^2}=0 \\ \frac{1}{2}=\frac{2}{x^2} \\ x^2=4 x=&pm;2$ pero ‘x > 0’

Entonces, x = 2

Ahora haremos el criterio de la segunda derivada,

g”(x)= $\frac{4}{x^3} \\ g''(2)=\frac{4}{2^3}=\frac{1}{2}>0$

Por lo tanto, x = 2 es un punto de mínimos locales.

Valor máximo local = g(2) = 2

(vii) 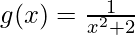$g(x)=\frac{1}{x^2+2}$

Solución:

Dado que, $g(x)=\frac{1}{x^2+2} \\ g'(x)=\frac{-1}{(x^2+2)^2}=0 \\ x=0$

Al diferenciar ambos lados de x, obtenemos

$g'(x)=\frac{-2x}{(x^2+2)^2}$

Ahora pon g'(x) = 0

$g'(x)=\frac{-2x}{(x^2+2)^2} = 0$

Ahora, realicemos la prueba de la segunda derivada,

$g''(x)=\frac{(x^2+2)^2(-2)+2x(x^2+2)}{(x^2+2)^4}\\ g''(x)=\frac{2^2(-2)+2(0)(2)}{(0+4)^2}$

= -8/16 = -1/2 < 0

En x = 0, g'(x) = 0 y g”(x) < 0

Por tanto, ‘x = 0’ es un punto de máximos locales.

Ahora el dominio de g(x) es (-∞, ∞).

$\lim_{x\to\infty} g(x)=0\space \& \space \lim_{x\to\infty} g(x)=0$

El valor de g(x) en los valores extremos de x es 0

Entonces el máximo global de g(x)= $\frac{1}{x^2}$ está en x = 0.

El valor máximo es g(0) = 1/2

(viii) 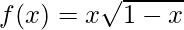$f(x)=x\sqrt{1-x}$ , x > 0

Solución:

Dado que, $f(x)=x\sqrt{1-x},x>0\\ f'(x)=\frac{x}{2\sqrt{1-x}}x-1+\sqrt{1-x}=\frac{-x+2(1-x)}{\sqrt{1-x}}=\frac{2-3x}{\sqrt{1-x}}$

Ahora pon f'(x) = 0

$\sqrt{1-x}=\frac{x}{2\sqrt{1-x}}$

2(1 – x) = x

2 – 2x = x

3x = 2

X = 2/3

Ahora vamos a hacer la prueba de la segunda derivada,

$f''(x)=\frac{\sqrt{1-x}(-3)-(2-3x).\frac{1}{2\sqrt{1-x}.(-1)}}{(1-x)}\\ f''(x)=\frac{-6(1-x)+(2-3x)}{2(1-x)^\frac{3}{2}}=\frac{3x-4}{(1-x)^{\frac{3}{2}}\\} \\f''(\frac{2}{3})=\frac{3.\frac{2}{3}-4}{(1-\frac{2}{3})^{\frac{3}{2}}}=\frac{-2}{(1/3)^{\frac{3}{2}}}<0$

x = 2/3 es un punto de máximos locales f(2/3) = $\frac{2}{3\sqrt{3}}$

Ahora, f (x) = x $x\sqrt{1-x},x>0$

Para dominio, 1 – x ≥ 0 o x ≤ 1

Entonces x ∈ [0, 1]

El máximo local está en x = 2/3 y el valor máximo local es $\frac{2}{3\sqrt{3}}$

Pregunta 4. Demuestra que las siguientes funciones no tienen máximos ni mínimos:

(i) f(x) = e ^x

Solución:

Dado que, f(x) = e ^x

f'(x) = e ^x

Ahora e ^x > 0, f'(x) > 0

Por lo tanto, f(x) es una función estrictamente creciente sin máximos ni mínimos.

(ii) g(x) = log x

Solución:

Dado que, g(x) = log x

g'(x) = 1/x

Ahora el dominio de log x es x > 0

Entonces, 1/x > 0, es decir, g'(x) > 0

Por lo tanto, g(x) es una función estrictamente creciente sin máximos ni mínimos.

(iii) h(x) = x3 ⁺ x2 + x ⁺ 1

Solución:

Dado que, h(x) = x ³ + x ² + x + 1

h'(x) = 3x ² + 2x + 1

Ahora para esta expresión cuadrática 3x ² + 2x + 1,

Su discriminante 0 = 2 ² – 4(3)(1) = -8 < 0

Entonces, 3x ² + 2x + 1 > 0

Por lo tanto, h(x) es una función estrictamente creciente sin máximos ni mínimos.

Pregunta 5. Encuentre el valor máximo absoluto y el valor mínimo absoluto de las siguientes funciones en los intervalos dados:

(i) f(x) = x ³ , x ∈ [-2, 2]

Solución:

Dado que, f(x) = x ³ , x ∈ [-2, 2]

f'(x) = 3x ²

f'(x) = 0 en x = 0

f”(x) = 6x

f”(0) = 0, fallo de la segunda derivada

Ahora f'(3 ⁺ ) > 0 y f'(3 ^– ) > 0

f'(x) no cambia de signo en x = 0.

x = 0 no es ni máximo ni mínimo

f(x) = x ³ es una función estrictamente creciente.

(ii) f(x) = sen x + cos x, x ∈ [0, π]

Solución:

Dado que, f(x) = sen x + cos x, x ∈ [0, π]

Primera derivada

f'(x) = cos x – sen x

Ahora pon f'(x) = 0

cos x = sen x

x = π/4

Al aplicar el criterio de la segunda derivada,

f”(x) = -sen x – cos x

f”(π/4) = $\frac{-1}{\sqrt2}-\frac{1}{\sqrt{2}}=-\sqrt{2}<0$

Por lo tanto, x = π/4 es p de máximos locales. f(π/4)= $\sqrt2$

Ahora, para máximos globales = max{f(0), f(π/4), f(π)}

= máx{1, √2, -1}

Porque el máximo global está en x = π/4 y el valor máximo global es √2.

Ahora, para mínimos globales = max{f(0), f(π/4), f(π)}

= máx{1, √2, -1}

Los mínimos globales están en x = π y el valor mínimo global es -1.

(iii) $f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]$

Solución:

Dado que, $f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]$

f'(x) = 4 – x

Ahora pon f'(x) = 0

4 – x = 0

x = 4

Ahora aplicando la prueba de la segunda derivada f”(x) = -1 < 0

Por lo tanto, x = 4 es un pt. de máximos locales.

f(4) = $4.4-\frac{4^2}{2}=8$

Máximos globales = max{f(-2), f(4), f(9/2)}

= máx{-10, 8, 7,8}

= 8

Los máximos globales ocurren en x = 9/2 y el valor máximo global es f(9/2) = 8

Mínimos globales = min{f(-2), f(4), f(9/2)}

= máx{-10, 8, 16,9}

= -10

Los mínimos globales ocurren en x = -2 y el valor mínimo global es f(-2) = -10.

(iv) f(x) = (x – 1) ² + 3, x ∈ [-3, 1]

Solución:

Dado que, f(x) = (x – 1) ² + 3, x ∈ [-3, 1]

f'(x) = 2(x – 1)

Ahora pon f'(x) = 0

2(x-1) = 0

X = 1

Ahora aplicando la prueba de la derivada de segundo orden,

f”(x) = 2 > 0

Por lo tanto, x = 1 es un punto de mínimos locales. f(1) = 3

Máximos globales = max{f(-3), f(1)}

= máx{19, 3}

= 19

El máximo global o absoluto ocurre en x = -3 y el valor máximo absoluto es f(-3) = 19

Mínimos globales = min{f(-3), f(1)}

= min{19, 3]

= 3

El mínimo global o absoluto ocurre en x = 1 y el valor absoluto es f(1) = 3

Pregunta 6. Encuentra la ganancia máxima que puede obtener una empresa, si la función de ganancia está dada por p(x) = 41 – 24x – 18x ²

Solución:

Dado que p(x) = 41 – 24x – 18x ²

p'(x) = -24 – 36x

Ahora pon p'(x) = 0

-24 – 36x = 0

x = -24/36

x = -2/3

Ahora, haciendo la prueba de la derivada de segundo orden,

p”(x) = -36 < 0

Por lo tanto, x = -2/3 es el punto de los máximos locales.

Ahora, en una función cuadrática con dominio R, si hay un máximo local, también es el máximo global. BC ₃ p(-∞)⇢ -∞ y p(+∞)⇢ -∞

La ganancia máxima es p(-2/3) = 49

Si no existen unidades negativas (x), entonces la ganancia máxima es p(0) = 41.

Pregunta 7. Encuentra tanto el valor máximo como el valor mínimo de 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en el intervalo [0, 3].

Solución:

Dado que f(x) = 3x ⁴ – 8x ³ + 12x ² – 48x + 25, x ∈ [0, 3]

f'(x) = 12x ² – 24x ² + 24x – 48

Ahora pon f'(x) = 0

12x ³ – 24x ² + 24x – 48 = 0

12(x ² – 2x ² + 2x – 4) = 0

12(x ² (x – 2) + 2(x – 2)) = 0

12(x ² + 2)(x – 2) = 0

x = 2 porque x ² + 2 ≠ 0

Ahora aplicando la prueba de la segunda derivada,

f”(x) = 12(3x ² – 4x + 2)

f”(2) = 12(3.2 ² – 4.2 + 2)

f”(2) = 12,6 = 72 > 0

Por lo tanto, x = 2 es el punto de mínimos locales.

f(2) = -39

Máximos globales = max{f(0), f(2), f(3)}

= máx{25, -39, 16}

= 25

Los máximos globales ocurren en x = 0 y el máximo global es 25.

Mínimos globales = min{f(0), f(2), f(3)}

= min{25, -39, 16}

= -39

Los mínimos globales ocurren en x = 2 y el valor mínimo global es -39.

Pregunta 8. ¿En qué puntos del intervalo [0, 2π] la función sen 2x alcanza su valor máximo?

Solución:

Dado que, f(x) = sen 2x , x ∈ [0, 2π]

f'(x) = 2 cos 2x

Ahora pon f'(x) = 0

2cos2x = 0

2x = (2x – 1)π/2

x = (2x – 1)π/4

x = π/4, 3π/4, 5π/4, 7π/4

Ahora hagamos la prueba de la derivada de segundo orden.

f”(x) = -4 sen2x

f”(π/4) = $-4\sin\frac{π}{2}=-4<0\\ f''(\frac{3π}{4})=-4\sin\frac{3π}{2}=+4>0\\ f''(\frac{5π}{4})=-4\sin\frac{5π}{2}=-4<0\\ f''(\frac{7π}{4})=-4\sin\frac{7π}{2}=+4>0$

x = π/4 y x = 5π/4 son puntos de máximos locales.

x = 3π/4 y x = 7π/4 son puntos de mínimos locales.

f(π/4) = f(5π/4) = 1 y f(3π/4) = f(7π/4) = -1

Ahora,

Máximos globales = max{f(0), f(π/4), f(3π/4), f{5π/4}, f(7π/4), f(2π)}

= máx{0, 1, -1, 1, -1, 0}

= 1

Los máximos globales ocurren en los puntos x = π/4 y x = 5π/4 y el valor máximo absoluto es 1.

Pregunta 9. ¿Cuál es el valor máximo de la función sen x + cos x?

Solución:

Dado que, f(x) = sen x + cos x

f'(x) = cos x – sen x

Ahora pon f'(x) = 0

cos x = sen x

$x=\frac{π}{4},\frac{-3π}{4},\frac{5π}{4},\frac{-7π}{4},\frac{8π}{4}........$

= {-√2, √2, +√2, -√2, -√2}

Ahora, prueba de derivadas de segundo orden,

f”(x) = -sen x – cos x

f”(π/4) = f”(9π/4) = f”(17π/4)………….. = -√2 < 0

Un litro ⇢ f(x) = sen x + cos x = $\sqrt{2}(\frac{1}{\sqrt{2}}\sin+\frac{1}{\sqrt{2}}\cos x)$

= $\sqrt{2}.\cos(\frac{π}{4}-x),f(x)_{max}=\sqrt{2}$

Pregunta 10. Encuentra el valor máximo de 2x ³ – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Solución:

Dado que f(x) = 2x ³ – 24x + 107

Al derivar wrt x obtenemos

f'(x) = 6x ² – 24

Ahora pon f'(x) = 0

6×2 ⁼ 24

× ² = 4

x = ±2

Ahora prueba de segundo orden

f”(x) = 12x

f”(2) = 12.2 = 24 > 0

x = 2 es un punto. de mínimos locales

f(2) = 75

f”(-2) = 12(-2) = -24 < 0

x = -2 es el punto de los máximos locales. f(-2) = 139

Ahora, en el intervalo [1, 3]

Máximos globales = max{f(1), f(2), f(3)}

= máx{85, 75, 89}

= 89

Ahora, en el intervalo [-3,-1]

Máximos globales = max{f(-3), f(-2), f(-1)}

= máx{125, 139, 129}

= 139

Pregunta 11. Se da que en x = 1, la función x ⁴ – 62x ² + ax + 9 alcanza su valor máximo en el intervalo [0, 2]. Encuentre el valor de a.

Solución:

Da eso, f(x) = x ⁴ – 62x ² + ax + 9

Al derivar wrt x obtenemos

f'(x) = 4x ³ – 124x + a

El valor máximo se alcanza en x = 1, y 1 se encuentra entre 0 y 2.

Entonces, en x = 1, debe haber un máximo local

Eso significa, f'(1) = 0

f'(1) = 4(1) ³ – 124(1) + a = 0

-120 + a = 0

un = 120

Pregunta 12. Encuentra los valores máximo y mínimo de x + sen2x en [0, 2π].

Solución:

Da que f(x) = x + sen2x, x ∈ [0, 2π]

Al derivar wrt x obtenemos

f'(x) = 1 + 2cos2x

Ahora pon f'(x) = 0, obtenemos

1 + 2cos2x = 0

cos2x = -1/2

$x=\frac{π}{3},\frac{2π}{3},\frac{4π}{3},\frac{5π}{3}$ ∈ [0, 2π]

Ahora,

Para máximos globales = max{f(0), f(π/3), f(4π/3), f(2π)}

= máx{0, π/3, $\frac{\sqrt{3}}{2},\frac{4π}{3}+\frac{\sqrt{3}}{2},2π$ }

= 2π

Los máximos globales ocurren en x = 2π y el valor máximo es f(2π) = 2π.

Para mínimos globales = min{f(0), f(2π/3), f(5π/3), f(2π)}

= min{0, $\frac{2π}{3}-\frac{\sqrt{3}}{2},\frac{5π}{3}-\frac{\sqrt{3}}{2},2π$ }

= 0

Los mínimos globales ocurren en x = 0 y el valor mínimo es 0.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.5 | Serie 1

Pregunta 1. Encuentra los valores máximo y mínimo, si los hay, de la siguiente función dada por

(yo) f(x) = (2x – 1) ² + 3

(ii) f(x) = 9x ² + 12x + 2

(iii) f(x) = -(x – 1) ² + 10

(iv) g(x) = x3 ⁺ 1

Pregunta 2. Encuentra los valores máximo y mínimo, si los hay, de las siguientes funciones dadas por

(yo) f(x) = |x + 2| – 1

(ii) g(x) = -|x + 1| + 3

(iii) h(x) = sen 2x + 5

(iv) f(x) = |sin(4x + 3)|

(v) h(x) = x + 1, x ∈ (-1, 1)

Pregunta 3. Encuentra los máximos locales y los mínimos locales, si los hay, de las siguientes funciones. Encuentre también los valores máximo local y mínimo local, según sea el caso:

(yo) f(x) = x ²

(ii) g(x) = x ³ – 3x

(iii) h(x) = sen x + cos x, 0 < x < π/2

(iv) f(x) = sen x – cos x, 0 < x < 2π

(v) f(x) = x ³ – 6x ² + 9x + 15

(vi) $g(x)=\frac{x}{2}+\frac{2}{x}$ , x > 0

(vii) $g(x)=\frac{1}{x^2+2}$

(viii) $f(x)=x\sqrt{1-x}$ , x > 0

Pregunta 4. Demuestra que las siguientes funciones no tienen máximos ni mínimos:

(i) f(x) = e ^x

(ii) g(x) = log x

(iii) h(x) = x3 ⁺ x2 + x ⁺ 1

Pregunta 5. Encuentre el valor máximo absoluto y el valor mínimo absoluto de las siguientes funciones en los intervalos dados:

(i) f(x) = x ³ , x ∈ [-2, 2]

(ii) f(x) = sen x + cos x, x ∈ [0, π]

(iii) $f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]$

(iv) f(x) = (x – 1) ² + 3, x ∈ [-3, 1]

Pregunta 6. Encuentra la ganancia máxima que puede obtener una empresa, si la función de ganancia está dada por p(x) = 41 – 24x – 18x ²

Pregunta 7. Encuentra tanto el valor máximo como el valor mínimo de 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en el intervalo [0, 3].

Pregunta 8. ¿En qué puntos del intervalo [0, 2π] la función sen 2x alcanza su valor máximo?

Pregunta 9. ¿Cuál es el valor máximo de la función sen x + cos x?

Pregunta 10. Encuentra el valor máximo de 2x ³ – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Pregunta 11. Se da que en x = 1, la función x ⁴ – 62x ² + ax + 9 alcanza su valor máximo en el intervalo [0, 2]. Encuentre el valor de a.

Pregunta 12. Encuentra los valores máximo y mínimo de x + sen2x en [0, 2π].

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra los valores máximo y mínimo, si los hay, de la siguiente función dada por

(yo) f(x) = (2x – 1) 2 + 3

(ii) f(x) = 9x 2 + 12x + 2

(iii) f(x) = -(x – 1) 2 + 10

(iv) g(x) = x3 + 1

Pregunta 2. Encuentra los valores máximo y mínimo, si los hay, de las siguientes funciones dadas por

(yo) f(x) = |x + 2| – 1

(ii) g(x) = -|x + 1| + 3

(iii) h(x) = sen 2x + 5

(iv) f(x) = |sin(4x + 3)|

(v) h(x) = x + 1, x ∈ (-1, 1)

Pregunta 3. Encuentra los máximos locales y los mínimos locales, si los hay, de las siguientes funciones. Encuentre también los valores máximo local y mínimo local, según sea el caso:

(yo) f(x) = x 2

(ii) g(x) = x 3 – 3x

(iii) h(x) = sen x + cos x, 0 < x < π/2

(iv) f(x) = sen x – cos x, 0 < x < 2π

(v) f(x) = x 3 – 6x 2 + 9x + 15

(vi) , x > 0

(vii)

(viii) , x > 0

Pregunta 4. Demuestra que las siguientes funciones no tienen máximos ni mínimos:

(i) f(x) = e x

(ii) g(x) = log x

(iii) h(x) = x3 + x2 + x + 1

Pregunta 5. Encuentre el valor máximo absoluto y el valor mínimo absoluto de las siguientes funciones en los intervalos dados:

(i) f(x) = x 3 , x ∈ [-2, 2]

(ii) f(x) = sen x + cos x, x ∈ [0, π]

(iii)

(iv) f(x) = (x – 1) 2 + 3, x ∈ [-3, 1]

Pregunta 6. Encuentra la ganancia máxima que puede obtener una empresa, si la función de ganancia está dada por p(x) = 41 – 24x – 18x 2

Pregunta 7. Encuentra tanto el valor máximo como el valor mínimo de 3x 4 – 8x 3 + 12x 2 – 48x + 25 en el intervalo [0, 3].

Pregunta 8. ¿En qué puntos del intervalo [0, 2π] la función sen 2x alcanza su valor máximo?

Pregunta 9. ¿Cuál es el valor máximo de la función sen x + cos x?

Pregunta 10. Encuentra el valor máximo de 2x 3 – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Pregunta 11. Se da que en x = 1, la función x 4 – 62x 2 + ax + 9 alcanza su valor máximo en el intervalo [0, 2]. Encuentre el valor de a.

Pregunta 12. Encuentra los valores máximo y mínimo de x + sen2x en [0, 2π].

Deja una respuesta Cancelar la respuesta

(yo) f(x) = (2x – 1) ² + 3

(ii) f(x) = 9x ² + 12x + 2

(iii) f(x) = -(x – 1) ² + 10

(iv) g(x) = x3 ⁺ 1

(yo) f(x) = x ²

(ii) g(x) = x ³ – 3x

(v) f(x) = x ³ – 6x ² + 9x + 15

(vi) $g(x)=\frac{x}{2}+\frac{2}{x}$ , x > 0

(vii) $g(x)=\frac{1}{x^2+2}$

(viii) $f(x)=x\sqrt{1-x}$ , x > 0

(i) f(x) = e ^x

(iii) h(x) = x3 ⁺ x2 + x ⁺ 1

(i) f(x) = x ³ , x ∈ [-2, 2]

(iii) $f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]$

(iv) f(x) = (x – 1) ² + 3, x ∈ [-3, 1]

Pregunta 6. Encuentra la ganancia máxima que puede obtener una empresa, si la función de ganancia está dada por p(x) = 41 – 24x – 18x ²

Pregunta 7. Encuentra tanto el valor máximo como el valor mínimo de 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en el intervalo [0, 3].

Pregunta 10. Encuentra el valor máximo de 2x ³ – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Pregunta 11. Se da que en x = 1, la función x ⁴ – 62x ² + ax + 9 alcanza su valor máximo en el intervalo [0, 2]. Encuentre el valor de a.