Capítulo 6 Aplicación de Derivadas – Ejercicio Misceláneo del Capítulo 6 | Serie 1
Pregunta 12. Un punto en la hipotenusa de un triángulo está a la distancia ayb de los lados del triángulo. Demuestre que la longitud mínima de la hipotenusa es 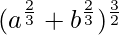
Solución:

Dado, un triángulo ABC
Sea PE = a y PD = b
En el △ABC, ∠B = 90
Sea ∠C = θ, entonces, ∠ DPA = θ
PD|| ANTES DE CRISTO.
Ahora en △ADDP,
cosθ = DP/AP = b/AP
AP = b/cosθ
En △EPC,
senθ = EP/CP = a/CP
CP = a/sen θ
Ahora AC = h = PA + PC
h =
h(θ) = b sec θ + a cosec θ
Poner h'(θ) =
b sen 3 θ = a cos 3 θ
tan3θ = a/b
tanθ = (a/b) 1/3
segθ =
cosecθ =
h máx =
h máx = (b 2/3 +a 2/3 ) 3/2
Pregunta 13. Encuentra los puntos en los que la función f dada por f (x) = (x – 2) 4 (x + 1) 3 tiene
(i) máximos locales
(ii) mínimos locales
(iii) punto de inflexión
Solución:
f(x) = (x – 2) 4 (x + 1) 3
Al derivar wrt x, obtenemos
f'(x) = 4(x – 2) 3 (x + 1) 3 + 3(x + 1) 2 (x – 2) 4
Pon f'(x) = 0
(x – 2) 3 (x + 1) 2 [4 (x + 1) + 3 (x – 2)] = 0
(x – 2) 3 (x + 1) 2 (7x – 2) = 0
Ahora,
Alrededor de x = -1, el signo no cambia, es decir
x = -1 es un punto de inflación
Alrededor de x = 2/7, el signo cambia de +ve a -ve, es decir,
x = 2/7 es un punto de máximos locales.
Alrededor de x = 2, el signo cambia de -ve a +ve, es decir,
x = 2 es un punto de mínimos locales
Pregunta 14. Encuentra los valores absolutos máximo y mínimo de la función f dada por f(x) = cos 2 x + sen x, x ∈ [0, π]
Solución:
f(x) = cos 2 x + sen x; x ϵ [0, π]
Al derivar wrt x, obtenemos
f'(x) = 2cos x(-sen x) + cos x = cos x – sen2x
Pon f'(x) = 0
cos x(1 – 2sen x) = 0
cos x = 0; sen x = 1/2
En x ϵ[0, π] si cos x = 0, entonces x = π/2
y si sen x = 1/2, entonces x = π/6 & 5π/6
Ahora, f”(x) = -sen x – 2 cos2x
f”(π/2) = -1 + 2 = 1 > 0
x = π/2 es un punto de mínimos locales f(π/2) = 1
f”(π/6) =
x = π/6 es un punto de máximos locales f(π/6) = 5/4
x = 5 π/6 es un punto de mínimos locales f(5 π/6) = 5/4
Máximos globales/absolutos = ma{f(0), f(π/6), f(π)}
= máx{1, 5/4, 1}
= 5/4 = valor máximo absoluto
Mínimos globales/absolutos = min{f(0), f(π/2), f(π/6), f(π)}
= min{1, 1, 5/4, 1}
= 1 = Valor mínimo absoluto
Pregunta 15. Demostrar que la altura del cono circular recto de máximo volumen que se puede inscribir en una esfera de radio r es 4π/3
Solución:
Sea ABC el cono
y o es el centro de la esfera.
AO = BO = CO = R
AO = h = altura del cono
BD = CD = r = radio del cono.
∠DOC = θ -(Propiedades del círculo)
En △ DOC,
OD = R cosθ & CD = Rsenθ,
r = R sen θ
AD = AO + OD = R + Rcosθ
h = R(1 + cosθ)
Ahora, el volumen del cono es
V =
v(θ) =
Poner v(θ) = 0
sen θ [2cos θ + 2cos 2 θ − sen2 θ ] = 0
sen θ [2cos θ + 2cos 2 θ − 1] = 0
sen θ (3cos θ − 1)(1 + cos θ ) = 0
sen θ = 0, cos = 1/3, cos θ = −1
Si senθ = 0, entonces el volumen será 0.
Si cosθ = -1, entonces sinθ = 0 y nuevamente el volumen será 0.
Pero si cosθ = 1/3; senθ = 2√2/3 y
Volumen, v = 32/81 πR 3 , que es máximo.
Altura, h = R(1 + cosθ) = R(
)
h = 4r/3
Por lo tanto probado
Pregunta 16. Sea f una función definida en [a, b] tal que f′(x) > 0, para todo x ∈ (a, b). Luego demuestre que f es una función creciente en (a, b).
Solución:
Dado que en [a, b] f'(x) > 0, para todo x en el intervalo I.
Así que consideremos x1, x2 pertenece a I con x1 < x2
Para probar: f(x) es creciente en (a, b)
Según el teorema de la media de Lagrange
f(x2) – f(x1)/ x2 – x1 = f'(c)
f(x2) – f(x1) = f'(c)(x2 – x1)
Donde x1 < c < x2
Como sabemos que x1 < x2
entonces x1 < x2 > 0
Se da que f'(x) > 0
entonces, f'(c) > 0
Por lo tanto, f(x2) – f(x1) > 0
f(x2) < f(x1)
Por lo tanto, para todo par de puntos x1, x2 pertenece a I con x1 < x2
f(x2) < f(x1)
f(x) es estrictamente creciente en I
Pregunta 17. Demuestra que la altura del cilindro de máximo volumen que se puede inscribir en una esfera de radio R es 2R/√3. Además, encuentre el volumen máximo.
Solución:
En △ABC,
CA 2 = BC 2 + AB 2
4R2 = 4r2 + h2 _
r 2 = R 2 –
……….(1)
Ahora, volumen del cilindro = πr 2 h
Ponga el valor de ov r 2 de eq(1), obtenemos
V = π(
).h
V(h) =
Al diferenciar ambos lados obtenemos
V'(h) =
Ahora pon V'(h) = 0
πR2 = _
Ahora el volumen máximo del cilindro = π[R 2 . 2R/√3 – 1/4,4R 2 /3,2R/ √3]
= 4πR 3 / 3√3
Pregunta 18. Demostrar que la altura del cilindro de mayor volumen que se puede inscribir en un cono circular recto de altura h y ángulo semivertical α es un tercio de la del cono y el mayor volumen del cilindro es 4/27 πh 3 tan 2 α .
Solución:

Dejar,
XQ = r
XO = h’
AO = h
CO = r’
∠XAQ = α
En el triángulo AXQ y AOC = XQ/OC = AX/AO
Entonces, r’/r = h-h’/h
hr’ = r(h-h’)
hr’ = rh – rh’
rh’ = rh – hr’
rh’ = h(r – r’)
h’ = h(r – r’)/r
El volumen del cilindro = πr’ 2 h’
v = πr’ 2 (h(r – r’)/r)
= π(h(rr’ 2 – r’ 3 )/r)
Al diferenciar obtenemos
v’ = πh/r(2rr’ – 3r’ 2 )
Nuevamente al diferenciar obtenemos
v” = πh/r(2r – 6r’) ………(1)
Ahora pon v’ = 0
πh/r(2rr’ – 3r’ 2 ) = 0
(2rr’ – 3r’ 2 ) = 0
2r’r = 3r’ 2
r’ = 2r/3
Entonces, v es máximo en r’ = 2r/3
El volumen máximo del cilindro = πh/r[r. 4r 2/9 – 8r 2/27 ]
= πhr 2 [4/27]
= 4/27πh(h tanα) 2
= 4/27πh 3 tan 2 α
Pregunta 19. Un tanque cilíndrico de 10 m de radio se llena con trigo a razón de 314 metros cúbicos por hora. Entonces la profundidad del trigo aumenta a razón de
(A) 1 m/h (B) 0,1 m/h (C) 1,1 m/h (D) 0,5 m/h
Solución:
Dado,
Radio del cilindro = 10 m [el radio es fijo]
Tasa de aumento de volumen = 314m 3 /h
es decir, dv/dt = 314m 3 /h
Ahora, el volumen del cilindro = πr 2 h
v = π.(10) 2 .h
v = 100πh
Al diferenciar wrt t, obtenemos
dv/dt = 100π
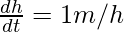
Entonces la opción A es correcta
Pregunta 20. La pendiente de la tangente a la curva x = t 2 + 3t – 8, y = 2t 2 – 2t – 5 en el punto (2,– 1) es
(A) 22/7 (B) 6/7 (C) 7/6 (D) -6/7
Solución:
Dado que la pendiente de la tangente a la curva x = t 2 + 2t – 8 y y = 2t 2 – 2t – 5
Al diferenciar obtenemos
Ahora, cuando x = 2,
t 2 + 3 – 8 = 2
t 2 + 3 – 10 = 0
t 2 – 2t + 5t – 10 = 0
(t – 2)(t + 5) = 0
Aquí, t = 2, t = -5 ……….(1)
Cuando y = -1
2t 2 – 2t – 5 = -1
2t 2 – 2t – 4 = 0
t 2 – t – 2 = 0
(t + 1)(t – 2) = 0
t = -1 o t = 2 ……….(2)
De eq(1) & eq(2) satisface ambos,
Ahora,
Entonces, la opción B es la correcta.
Pregunta 21. La recta y = mx + 1 es tangente a la curva y 2 = 4x si el valor de m es
(A) 1 (B) 2 (C) 3 (D)1/2
Solución:
La curva si y 2 = 4x …….(1)
Al diferenciar obtenemos
La pendiente de la tangente a la curva dada en el punto (x, y)
m = 2/año
y = 2/m
La ecuación de la recta es y = mx + 1
Ahora pon el valor de y, obtenemos el valor de x
2/m = mx + 1
x = 2 – m/m
Ahora pon el valor de y y x en la ecuación (1), obtenemos
(2/m) 2 = 4(2 – m/m)
metro = 1
Por lo tanto, la opción A es correcta.
Pregunta 22. La normal en el punto (1, 1) de la curva 2y + x 2 = 3 es
(A) x + y = 0 (B) x – y = 0
(C) x + y +1 = 0 (D) x – y = 1
Solución:
La ecuación de la curva 2y + x 2 = 3
Al derivar wrt x, obtenemos
2
dy/dx = -x
La pendiente de la tangente a la curva dada en el punto (1, 1)
dy/dx = -x = -1
metro = -1
Y pendiente de normal = 1
Ahora la ecuación de la normal
(y-1) = 1(x-1)
x – y = 0
Entonces, la opción B es correcta
Pregunta 23. La normal a la curva x 2 = 4y pasando (1, 2) es
(A) x + y = 3 (B) x – y = 3 (C) x + y = 1 (D) x – y = 1
Solución:
La ecuación de la curva es x 2 = 4y …….(1)
Al derivar wrt x, obtenemos
2x =
La pendiente de la normal en (x, y)
-dx/dy = -2/x = m
La pendiente en el punto dado (1, 2)
m = (y – 2)/(x – 1)
-2/x = (y – 2)/(x – 1)
y = 2/x
Ahora pon el valor de y en la ecuación (1)
x2 = 4( 2 /x)
x = 2
y y = 1
Entonces el punto es (2, 1)
Ahora la pendiente de la normal en el punto (2, 1) = -2/2 = -1
La ecuación de la normal es
(y-1) = -1(x-2)
x + y = 3
Entonces la opción A es correcta
Pregunta 24. Los puntos en la curva 9y 2 = x 3 , donde la normal a la curva hace intersecciones iguales con los ejes son
(A) 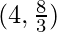 (B)
(B) 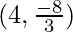
(C)  (D)
(D)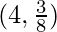
Solución:
Dada la ecuación 9y 2 = x 3
Al derivar wrt x, obtenemos
18y dy/dx = 3x 2
dy/dx = 3x 2 /18y
dy/dx = x 2 /6y
Ahora, la pendiente de la normal a la curva dada en el punto (x 1 , y 1 ) es
Por lo tanto, la ecuación de la normal a la curva en el punto (x 1 , y 1 ) es
De acuerdo a la pregunta se da que lo normal
hacer intersecciones iguales con los ejes.
Asi que,
…………(1)
El punto (x 1 , y 1 ) se encuentra en la curva,
…………(2)
De la ecuación (1) y (2), obtenemos
De la ecuación (2), obtenemos
Por lo tanto, los puntos requeridos son
Entonces, la opción A es correcta.
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA