Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 6 Aplicación de derivadas – Ejercicio misceláneo en el Capítulo 6

Pregunta 1. Usando diferenciales, encuentre el valor aproximado de cada uno de los siguientes:

(yo) (17/81) ^1/4

(ii) 33 ^-1/5

Solución:

(yo) (17/81) ^1/4

Sean y = x ^1/4 , x = 16/81 y △x = 1/81

△y = (x + △x) ^1/4 – x ^1/4

= (17/81) ^1/4 – (16/81) ^1/4

= (17/81) ^1/4 – (2/3)

Asi que,

(17/81) ^1/4 = (2/3) + △y

Aquí, dy es aproximadamente igual a △y

dy = (dy/dx)△x

= $\frac{1}{4x^{\frac{3}{4}}}(△x)$

= $\frac{1}{4(\frac{16}{81})^{\frac{3}{4}}}(\frac{1}{81})$

= 27/32 × 1/81

= 1/96

= 0.010

Por lo tanto, el valor aproximado de (17/81) ^1/4 = 2/3 + 0,010 = 0,677

(ii) 33 ^-1/5

Sean y = x ^-1/5 , x = 32 y △x = 1

△y = (x + △x) ^-1/5 – x ^-1/5

= (33) ^-1/5 – (32) ^-1/5

= (33) ^-1/5 – 1/2

Asi que,

(33) ^-1/5 = 1/2 + △y

Aquí, dy es aproximadamente igual a △y

dy = (dy/dx)△x

= $\frac{-1}{5x^{\frac{6}{5}}}(△x)$

= $\frac{-1}{5(32)^{\frac{6}{5}}}(1)$

= -1/320

= -0.003

Por tanto, el valor aproximado de (33) ^-1/5 = 1/2 – 0,003 = 0,497

Pregunta 2. Muestre que la función dada por f(x) = log x/x tiene un máximo en x = e.

Solución:

La función dada es f(x) = log x/x

$f'(x)=\frac{x(\frac{1}{x})-\log x}{x^2}=\frac{1-\log x}{x^2}$

Ahora, f'(x) = 0

1 – logaritmo x = 0

registro x = 1

registro x = registro e

x = mi

Ahora, $f''(x)=\frac{x^2(-\frac{1}{x})-(1-\log x)(2x)}{x^4}$

$=\frac{-x-2x(1-\log x}{x^3}$

$=\frac{-3+3\log x}{x^3}$

$f''(e)=\frac{-3+2\log e}{e^3}=\frac{-3+2}{e^3}=\frac{-1}{e^3}<0$

Por lo tanto, por la prueba de las segundas derivadas, f es el máximo en x = e.

Pregunta 3. Los dos lados iguales de un triángulo isósceles con base fija b están decreciendo a razón de 3 cm por segundo. ¿Qué tan rápido disminuye el área cuando los dos lados iguales son iguales a la base?

Solución:

Dado un triángulo isósceles con base fija b.

Sean los otros dos lados de longitud x.

Ahora se da eso,

dx/dy = -3cm/s

Ahora semiperímetro(s) = x + x + b/2

s = x + b/2

Área [por la fórmula de garza] = $\sqrt{s(s-x)(s-x)(s-b)}$

$A=(s-x).\sqrt{s(s-b)}$

$A=\frac{b}{2}\sqrt{(x+\frac{b}{2})(x-\frac{b}{2})}$

$A=\frac{b}{2}\sqrt{x^2}\frac{-b^2}{2}$

$A=\frac{b}{4}\sqrt{4x^2-b^2}$

Para encontrar: dA/dt = ?

DA/dt = ?

$\frac{dA}{dt}=\frac{b}{4}.\frac{1}{2\sqrt{4x^2-b^2}}.8x.\frac{dx}{dt}$

$\frac{dA}{dt}=\frac{b}{4}.\frac{1}{2b\sqrt{3}}.8b.(-3)$

dA/dt = -√3b cm2 ^/ s

Por lo tanto, el área está disminuyendo a razón = √3b cm ² /s

Pregunta 4. Encuentra la ecuación de la normal a la curva x ² = 4y que pasa por el punto (1, 2).

Solución:

Área dada: x ² = 4y

Al derivar ambos lados con respecto a y,

2x(dx/día) = 4

dx/dy = 2/x

Pendiente = -1/m = -2/x

Por punto pendiente forma ecuación de normal será,

y-2 = -1(x-1)

x + y = 3 es la ecuación requerida de normal.

Pregunta 5. Muestre que la normal en cualquier punto θ a la curva x = acosθ + aθsinθ, y = asinθ – aθ cosθ está a una distancia constante del origen.

Solución:

Curva dada,

x = acosθ + aθsen θ

y = asinθ – aθcos θ

Ahora -dx/dy = pendiente de normal = $\frac{\frac{-dx}{dθ}}{\frac{dy}{dθ}}$ -(1)

$\frac{dx}{dθ}$ = -asinθ + asinθ + aθcosθ

$\frac{dx}{dθ}$ = aθcosθ -(2)

$\frac{dx}{dθ}$ = acosθ + aθsinθ – acosθ

$\frac{dx}{dθ}$ = aθsenθ -(3)

$\frac{-dx}{dy}=\frac{-aθ\cos θ}{aθ\sin θ}$ -(De 1, 2 y 3)

-dx/dy = -cotθ

Ahora usando la pendiente del punto desde, la ecuación de la normal será,

$y-a\sin θ+aθ\cos θ=\frac{-\cos θ}{\sin θ}(x-a\cos θ-aθ\sinθ)$

ysinθ – asin ^-2 θ + aθcosθsinθ = -xcosθ + acos ² θ + aθsinθcosθ

y sen θ + y sen θ − a = 0

$d=\frac{|0+0-a|}{\sqrt{\cos^2θ+\sin^2θ}}=a=$ constante.

Por lo tanto probado

Pregunta 6. Encuentra los intervalos en los que la función f dada por $f(x)=\frac{4\sin x-2x-x\cos x}{2t\cos x}$ es

(i) creciente (ii) decreciente

Solución:

$f(x)=\frac{4\sin x-2x-x\cos x}{2+\cos x}$

$f'(x)=\frac{(2+\cos x)(4\cos x-2+x\sin x-\cos x)+(4\sin x-2x-x-\cos x)(\sin x)}{(2+\cos x)^2}$

$f'(x)=\frac{4\cos x-cos^2x}{(2+\cos x)^2}$

(i) Para f(x) tp sea creciente f'(x) ≥ 0

$\frac{4\cos x-cos^2x}{(2+\cos x)^2}>0$

$\cos x(4-\cos x)>0$

Ahora, 4 – cos x > 0 -(porque 4 – cos x ≥ 3)

Entonces, cos x > 0

Por lo tanto, f(x) es creciente para 0 < x < x/2 y 3π/2 < x < 2π

(ii) Para que f(x) sea decreciente,

f'(x) < 0

$\frac{4\cos x-\cos^2x}{(\cos x+2)^2}<0$

cos x (4 − cos x ) < 0

porque x < 0

Por lo tanto, f(x) es decreciente para π/2 < x < 3π/2

Pregunta 7. Encuentra los intervalos en los que la función f dada por f(x)= 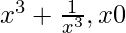$x^3+\frac{1}{x^3},x≠0$ es

(i) creciente (ii) decreciente

Solución:

f(x) = $x^3+\frac{1}{x^3},x≠ 0$

f'(x) $=3x^2-\frac{1}{3x^4}$

(i) Para que f(x) sea creciente,

f'(x) > 0

$3x^2-\frac{1}{3x^4}>0$

$\frac{9x^6-1}{3x^4}>0$

9x ⁶ > 1

$x>(\frac{1}{9})^{\frac{1}{6}}$ o $x∈((\frac{1}{9}^{\frac{1}{6}}),∞)$

(ii) Para que f(x) sea decreciente,

f'(x) < 0 $3x^2-\frac{1}{3x^4}<0$

9x ⁶ < 1

$x<(\frac{1}{9})^{\frac{1}{6}}$ o $x∈(∞,(\frac{1}{9}^{\frac{1}{6}}))$

Pregunta 8. Encuentra el área máxima de un triángulo isósceles inscrito en la elipse 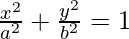$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ con su vértice en un extremo del eje mayor.

Solución:

Dada la elipse: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Su eje mayor es el eje x.

Usando la forma paramétrica de elipse, x = acosθ, y = bsinθ,

Si las coordenadas de A son (acosθ, bsinθ)

Entonces las coordenadas de B’S serán (acosθ, -bsin θ).

Ahora, OC = a, OD = acos θ, entonces CD = a(1 + cos θ)

AB = |AD| + |BD| = 2b sen θ

Área de △ABC = 1/2.AB.CD

= 1/2.2bsen θ.a(1 + cos θ)

△(θ) = ab.senθ.(1 + sen θ)

Para máximos/mínimos, ponga △'(θ) = 0

△'(θ) = ab[cosθ[1 + cosθ] + sinθ[-sinθ]]

△'(θ) = ab[2cos ² θ + cosθ – 1] = 0

2 cos ² θ + cos θ – 1 = 0

2 cos ² θ + 2 cos θ – cos θ – 1 = 0

2cosθ(cosθ + 1) – 1(cosθ + 1) = 0

(2cosθ – 1).(cosθ + 1) = 0

cosθ = 1/2 o cosθ = -1

Si cosθ = -1, entonces senθ = 0 y △(θ) = 0

Pero si cosθ = 1/2, sinθ = √3/2 & △(θ) = ab. $\frac{\sqrt{3}}{2}(1+\frac{1}{2})$

$△(θ)_{max}=\frac{2\sqrt{3}ab}{4}$

Pregunta 9. Se va a construir un tanque con base rectangular y lados rectangulares, abierto en la parte superior de modo que su profundidad sea de 2 my el volumen de 8 m3. Si la construcción del tanque cuesta 70 rupias por metro cuadrado para la base y 45 rupias por metro cuadrado para los lados. ¿Cuál es el costo del tanque menos costoso?

Solución:

Dado:

Profundidad del tanque = 2m

Volumen = 8m ³

Sea el largo igual a x y el ancho igual a y

El área de la base será igual a xy

El área de los lados será igual a; 2x, 2y, 2x, 2y

Ahora, volumen = xy2 = 2xy = 8m ³

entonces, xy = 4m ² -(1)

y = 4/x

Costo total = 70.base + 45.(lados)

c = 70xy + 45(2x + 2y + 2x + 2y)

c = 70.4 + 45.4(x + y) -(xy = 4)

c(x) = 180 – \ $\frac{180.4}{x^2}=0$

$1-\frac{4}{x^2}=0$

× ² = 4

x = ±2, x = 2, (Rechazando el valor -ve)

y = 4/x = 4/2 = 2

Ahora cuesta c(x) = 280 + 180(x + 4/x)

c = 280 + 180 (2 + 2)

c = 1000 rupias

Pregunta 10. La suma del perímetro de un círculo y un cuadrado es k, donde k es una constante. Demostrar que la suma de sus áreas es mínima cuando el lado del cuadrado es el doble del radio del círculo.

Solución:

Sean x los lados del cuadrado y r el radio del círculo.

Perímetro del cuadrado = 4x

Circunferencia del círculo = 2πr

Ahora dado que, 4x + 2πr = k -(1)

x = $\frac{k-2πr}{4}$

Área del cuadrado = x ²

Área del círculo = πr ²

Suma de áreas = x ² + πr ²

$s(r)=(\frac{k-2πr}{4})^2+πr^2$

Ponga s'(r) = 0

$s(r)=2(\frac{k-2πr}{4})(\frac{-π}{2})+2πr=0$ -(De la ecuación (1))

$πr=\frac{π}{2}\frac{k-2πr}{4}$

8πr = kπ – 2π ² r

8r = k – 2πr

8r = (4x + 2πr) – 2πr -(k = 4x + 2πr)

8r = 4x

x = 2r

Por lo tanto, se demostró que los lados del cuadrado son el doble del radio del círculo.

Pregunta 11. Una ventana tiene la forma de un rectángulo coronado por una abertura semicircular. El perímetro total de la ventana es de 10 m. Encuentre las dimensiones de la ventana para admitir la máxima luz a través de toda la abertura.

Solución:

Sea la longitud del rectángulo = x

el ancho del rectángulo = y

y el radio del semicírculo = x/2

Entonces, dado que el perímetro total de la ventana = 10 m

PAG = πx/2 + x + 2y = 10

x(1 + π/2) + 2y = 10

2y = 10 – x(1 + π/2)

y = 5 – x(1/2 – π/4) -(1)

Ahora, el área de la ventana

$A=\frac{πx^2}{2}+xy$ -(2)

De eq(1) ponemos el valor de y en eq(2), obtenemos

$A=x.[5 - x(\frac{1}{2} - \frac{π}{4})]+\frac{πx^2}{2}$

= 5x – x ² (1/2 + π/4) + πx ² /8

Al diferenciar obtenemos

A’ = 5 – 2x(1/2 + π/4) + 2xπ/8

= 5 – x(1 + π/2) + xπ/4

Ponga A’ = 0

5 – x(1 + π/2) + xπ/4 = 0

-x(1 + π/2) + xπ/4 = -5

x(-1 – π/2 + π/4) = -5

x(-1 – π/2 + π/4) = -5

x(1 + π/4) = 5

x = 5/ (1 + π/4)

x = 20/ π + 4

Por lo tanto, la longitud del rectángulo = 20/ π + 4

Ahora pon el valor de x en la ecuación (1)

y = 5 – (20/ π + 4)(1/2 – π/4)

y = 10/π + 4

Por lo tanto, ancho del rectángulo = 10/π + 4

y el radio del semicírculo = x/2 = $\frac{\frac{20}{π + 4}}{2}$ = 10/π + 4

Capítulo 6 Aplicación de Derivadas – Ejercicio Misceláneo del Capítulo 6 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 6 Aplicación de derivadas – Ejercicio misceláneo en el Capítulo 6 | Serie 1

Pregunta 1. Usando diferenciales, encuentre el valor aproximado de cada uno de los siguientes:

(yo) (17/81) ^1/4

(ii) 33 ^-1/5

Pregunta 2. Muestre que la función dada por f(x) = log x/x tiene un máximo en x = e.

Pregunta 3. Los dos lados iguales de un triángulo isósceles con base fija b están decreciendo a razón de 3 cm por segundo. ¿Qué tan rápido disminuye el área cuando los dos lados iguales son iguales a la base?

Pregunta 4. Encuentra la ecuación de la normal a la curva x ² = 4y que pasa por el punto (1, 2).

Pregunta 5. Muestre que la normal en cualquier punto θ a la curva x = acosθ + aθsinθ, y = asinθ – aθ cosθ está a una distancia constante del origen.

Pregunta 6. Encuentra los intervalos en los que la función f dada por $f(x)=\frac{4\sin x-2x-x\cos x}{2t\cos x}$ es

(i) creciente (ii) decreciente

Pregunta 7. Encuentra los intervalos en los que la función f dada por f(x)= $x^3+\frac{1}{x^3},x≠0$ es

(i) creciente (ii) decreciente

Pregunta 8. Encuentra el área máxima de un triángulo isósceles inscrito en la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ con su vértice en un extremo del eje mayor.

Pregunta 10. La suma del perímetro de un círculo y un cuadrado es k, donde k es una constante. Demostrar que la suma de sus áreas es mínima cuando el lado del cuadrado es el doble del radio del círculo.

Pregunta 11. Una ventana tiene la forma de un rectángulo coronado por una abertura semicircular. El perímetro total de la ventana es de 10 m. Encuentre las dimensiones de la ventana para admitir la máxima luz a través de toda la abertura.

Capítulo 6 Aplicación de Derivadas – Ejercicio Misceláneo del Capítulo 6 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Usando diferenciales, encuentre el valor aproximado de cada uno de los siguientes:

(yo) (17/81) 1/4

(ii) 33 -1/5

Pregunta 2. Muestre que la función dada por f(x) = log x/x tiene un máximo en x = e.

Pregunta 3. Los dos lados iguales de un triángulo isósceles con base fija b están decreciendo a razón de 3 cm por segundo. ¿Qué tan rápido disminuye el área cuando los dos lados iguales son iguales a la base?

Pregunta 4. Encuentra la ecuación de la normal a la curva x 2 = 4y que pasa por el punto (1, 2).

Pregunta 5. Muestre que la normal en cualquier punto θ a la curva x = acosθ + aθsinθ, y = asinθ – aθ cosθ está a una distancia constante del origen.

Pregunta 6. Encuentra los intervalos en los que la función f dada por es

(i) creciente (ii) decreciente

Pregunta 7. Encuentra los intervalos en los que la función f dada por f(x)= es

(i) creciente (ii) decreciente

Pregunta 8. Encuentra el área máxima de un triángulo isósceles inscrito en la elipse con su vértice en un extremo del eje mayor.

Pregunta 10. La suma del perímetro de un círculo y un cuadrado es k, donde k es una constante. Demostrar que la suma de sus áreas es mínima cuando el lado del cuadrado es el doble del radio del círculo.

Pregunta 11. Una ventana tiene la forma de un rectángulo coronado por una abertura semicircular. El perímetro total de la ventana es de 10 m. Encuentre las dimensiones de la ventana para admitir la máxima luz a través de toda la abertura.

Capítulo 6 Aplicación de Derivadas – Ejercicio Misceláneo del Capítulo 6 | conjunto 2

Deja una respuesta Cancelar la respuesta

(yo) (17/81) ^1/4

(ii) 33 ^-1/5

Pregunta 4. Encuentra la ecuación de la normal a la curva x ² = 4y que pasa por el punto (1, 2).

Pregunta 6. Encuentra los intervalos en los que la función f dada por $f(x)=\frac{4\sin x-2x-x\cos x}{2t\cos x}$ es

Pregunta 7. Encuentra los intervalos en los que la función f dada por f(x)= $x^3+\frac{1}{x^3},x≠0$ es

Pregunta 8. Encuentra el área máxima de un triángulo isósceles inscrito en la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ con su vértice en un extremo del eje mayor.