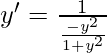Clase 12 Soluciones NCERT – Matemáticas Parte II – Capítulo 9 Ecuaciones diferenciales – Ejercicio -9.2

En cada una de las Preguntas 1 a 6 verifique que las funciones dadas (explícitas) sean una solución de la ecuación diferencial correspondiente:

Pregunta 1. y = e ^x + 1 : y” – y’ = 0

Solución:

Dado: y = e ^x + 1

Al diferenciar obtenemos

y’ = e ^x -(1)

Nuevamente diferenciando obtenemos

y” = e ^x -(2)

Ahora sustituya los valores de la ecuación (1) y (2), en la ecuación diferencial

y” – y’ = e ^x – e ^x = 0

Por lo tanto verificado

Pregunta 2. y = x ² + 2x + C : y’ – 2x – 2 = 0

Solución:

Dado: y = x ² + 2x + C

Al diferenciar obtenemos

y’ = 2x + 2

y’ – 2x – 2 = 0

Por lo tanto verificado

Pregunta 3. y = cosx + c : y’ + sen x = 0

Solución:

Dado: y = cos x + c

Al diferenciar obtenemos

y’ = -sen x -(1)

Ahora sustituya los valores de la ecuación (1), en la ecuación diferencial

y’ + sen x = 0

-sen x + sen x = 0

0 = 0

Por lo tanto verificado

Pregunta 4. 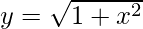$y=\sqrt{1+x^{2}}$ : $y'=\frac{xy}{1+x^{2}}$

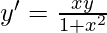
Solución:

Dado: $y=\sqrt{1+x^{2}}$

$y'=\frac{1}{2\sqrt{1+x^2}}.2x=\frac{x}{\sqrt{1+x^2}}=\frac{x.\sqrt{1+x^2}}{1+x^2}=\frac{xy}{1+x^2}$

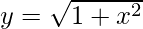
Pregunta 5. y = Ax : xy’ = y (x ≠ 0)

Solución:

Dado: y = Ax

y/A = x -(1)

Al diferenciar obtenemos

y’ = A -(2)

Ahora sustituya los valores de la ecuación (1) y (2), en la ecuación diferencial

xy’ = y

$\frac{y}{A}A$ = y

y = y

Por lo tanto verificado

Pregunta 6. y = x sen x : xy’ = y + x 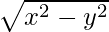$\sqrt{x^2-y^2}$ (x ≠ 0 y x > y o x < -y)

Solución:

Dado: y = x.sen x

Al diferenciar obtenemos

y’ = x cos x + sen x -(1)

Ahora sustituya los valores de la ecuación (1), en la ecuación diferencial

Tomando LHS

xy’ = x(x cos x + sen x)

= x ² cos x + x sen x

= x ² √1 – sen ² x + y

= y + ^x2 $\sqrt{1 - (\frac{y}{x})^2}$

= y + ^x2 $\frac{\sqrt{x^2 - y^2}}{x}$

= y + x $\frac{\sqrt{x^2 - y^2}}{x}$

LHS = RHS

Por lo tanto verificado

Pregunta 7. xy = log y + C : y’ = $\frac{y^{2}}{1-xy}(xy≠1)$

Solución:

Dado: xy = logía + C -(1)

Al diferenciar obtenemos

xy’ + y = $\frac{1}{y}$ > y’

xyy’ + y2 ⁼ y’

xyy’ – y’ = -y ²

y'(xy – 1) = -y ²

y’ = -y ² / (xy – 1) -(2)

Ahora sustituya los valores de la ecuación (1) y (2), en la ecuación diferencial

y’ = $\frac{y^{2}}{1-xy}$

$\frac{-y^2}{-(1 - xy)} = \frac{y^{2}}{1-xy}$

$\frac{y^2}{1 - xy} = \frac{y^{2}}{1-xy}$

Por lo tanto verificado

Pregunta 8. y – cos y = x : (y sen y + cos y + x)y’ = y

Solución:

Dado: y – cos y = x -(1)

Al diferenciar obtenemos

y’ – sen y.y’ = 1

y'(1 + sen y) = 1

$y' = \frac{1}{(1 + sin y)}$ -(2)

Ahora sustituya los valores de la ecuación (1) y (2), en la ecuación diferencial

(y sen y + cos y + x) y’ = y

$(y sin y + cos y + y - cosy)\frac{1}{1+siny} = y$

$(y sin y + y)\frac{1}{1+siny} = y$

$y(sin y + 1)\frac{1}{1+siny} = y$

y = y

Por lo tanto verificado

Pregunta 9. x + y = tan ^-1 y : y ² y’ + y ² + 1 = 0

Solución:

Dado: x + y = tan ^-1 y

Al diferenciar obtenemos

1 + y’ = $\frac{1}{1+y^2}y'$

$y'[\frac{1}{1+y^2}-1]=1$

$y'[\frac{1-1+y^2}{1+y^2}]=1$

$y'[\frac{-y^2}{1+y^2}]=1$

$y'=\frac{1}{\frac{-y^2}{1+y^2}}$

$y'=\frac{-(1+y^2)}{y^2}$ -(1)

Ahora sustituya los valores de la ecuación (1), en la ecuación diferencial

y ² y’ + y ² + 1 = 0

$y^2[\frac{-(1+y^2)}{y^2}] + y^2 + 1 = 0$

$-1-y^2 + y^2 + 1 = 0$

0 = 0

Por lo tanto verificado

Pregunta 10. $y=\sqrt{a^2-x^2}x∈(-a,a)$ : $x+y\frac{dy}{dx}=0(y≠0)$

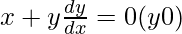
Solución:

Dado: $y=\sqrt{a^2-x^2}$

También podemos escribir como

y ² = un ² – x ²

Ahora al diferenciar obtenemos

2yy’ = -2x

y’ = -2x/2y

y’ = -x/y -(1)

Ahora sustituya los valores de la ecuación (1), en la ecuación diferencial

x + y. $\frac{dy}{dx}=0$

x + y (-x/y) = 0

x – x = 0

0 = 0

Por lo tanto verificado

Pregunta 11. El número de constantes arbitrarias en la solución general de una ecuación diferencial de cuarto orden son

(A) 0 (B) 2 (C) 3 (D)4

Solución:

(D) es la respuesta correcta porque el número de constantes en la solución general de una ecuación diferencial de orden n es igual a su orden.

Pregunta 12. El número de constantes arbitrarias en la solución particular de una ecuación diferencial de tercer orden son:

(A) 3 (B) 2 (C) 1 (D) 0

Solución:

(D) es la respuesta correcta porque no hay constantes arbitrarias en una solución particular.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

En cada una de las Preguntas 1 a 6 verifique que las funciones dadas (explícitas) sean una solución de la ecuación diferencial correspondiente:

Pregunta 1. y = e x + 1 : y” – y’ = 0

Pregunta 2. y = x 2 + 2x + C : y’ – 2x – 2 = 0

Pregunta 3. y = cosx + c : y’ + sen x = 0

Pregunta 4. :

Pregunta 5. y = Ax : xy’ = y (x ≠ 0)

Pregunta 6. y = x sen x : xy’ = y + x (x ≠ 0 y x > y o x < -y)

Pregunta 7. xy = log y + C : y’ =

Pregunta 8. y – cos y = x : (y sen y + cos y + x)y’ = y

Pregunta 9. x + y = tan -1 y : y 2 y’ + y 2 + 1 = 0

Pregunta 10. :

Pregunta 11. El número de constantes arbitrarias en la solución general de una ecuación diferencial de cuarto orden son

(A) 0 (B) 2 (C) 3 (D)4

Pregunta 12. El número de constantes arbitrarias en la solución particular de una ecuación diferencial de tercer orden son:

(A) 3 (B) 2 (C) 1 (D) 0

Deja una respuesta Cancelar la respuesta

Pregunta 1. y = e ^x + 1 : y” – y’ = 0

Pregunta 2. y = x ² + 2x + C : y’ – 2x – 2 = 0

Pregunta 4. $y=\sqrt{1+x^{2}}$ : $y'=\frac{xy}{1+x^{2}}$

Pregunta 6. y = x sen x : xy’ = y + x $\sqrt{x^2-y^2}$ (x ≠ 0 y x > y o x < -y)

Pregunta 7. xy = log y + C : y’ = $\frac{y^{2}}{1-xy}(xy≠1)$

Pregunta 9. x + y = tan ^-1 y : y ² y’ + y ² + 1 = 0

Pregunta 10. $y=\sqrt{a^2-x^2}x∈(-a,a)$ : $x+y\frac{dy}{dx}=0(y≠0)$