Clase 12 Soluciones NCERT – Matemáticas Parte II – Capítulo 9 Ecuaciones diferenciales – Ejercicio -9.3

En cada uno de los ejercicios 1 a 5, a partir de una ecuación diferencial que represente la familia de curvas dada eliminando las restricciones arbitrarias a y b.

Pregunta 1.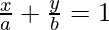 $\frac{x}{a}+\frac{y}{b}=1$

Solución:

Dado: $\frac{x}{a}+\frac{y}{b}=1$

También podemos escribir

bx + ay = ab

Al diferenciar obtenemos

b + ay’ = 0

y’ = -b/a

Nuevamente diferenciando obtenemos

y” = 0

Pregunta 2. 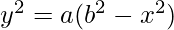$y^2=a(b^2-x^2)$

Solución:

Dado: $y^2=a(b^2-x^2)$

Al diferenciar obtenemos

2y.y’=-2ax

$\frac{yy'}{x}=-a$

Nuevamente diferenciando obtenemos

$\frac{x[yy''+(y')2]-yy'}{x^2}=0$

xyy” + x(y’) ² – yy’ = 0

Pregunta 3. y = ae ^3x +be ^-2x

Solución:

y = ae ^3x + be ^-2x -(1)

Al diferenciar obtenemos

y’=3ae ^3x -2be ^-2x -(2)

Nuevamente diferenciando obtenemos

y”=9ae ^3x +4be ^2x

Ahora en multiplicar eq(1) por 6

6y = 6ae ^3x + 6be ^-2x

Y sumamos con eq(2)

6y + y’ = 6ae ^3x + 6be ^-2x + 3ae ^3x – 3be ^-2x

6y + y’ = 9ae ^3x + 4be ^-2z = y”

y” – y’ – 6y = 0

Pregunta 4. y = e ^2x (a + bx)

Solución:

Dado: y = e ^2x (a + bx) -(1)

Al diferenciar obtenemos

y’ = e ^2x (b) + (a + bx).2e ^2x

y’ = e ^2x (b + 2a + 2bx) -(2)

Ahora en multiplicar eq(1) por 2

2y = e ^2x (2a + 2bx)

Y sumamos con eq(2)

y’ – 2y = e ^2x (b + 2a + 2bx) – e ^2x (2a + 2bx)

y’ – 2y = ser ^2x -(3)

Nuevamente diferenciando obtenemos

y” – 2y’ = 2be ^2x

Ahora pon el valor de be ^2x de eq(3)

y” – 2y’ = 2(y’ – 2y)

y” – 2y’ = 2y’ – 4y

y” – 2y’ – 2y’ + 4y = 0

y” – 4y’ + 4y = 0

Pregunta 5. $y=e^x(a\cos x+b\sin x)$

Solución:

Dado: y = e ^x (a cos x + b sen x) -(1)

Al diferenciar obtenemos

y’ = e ^x [a cos x + b sen x – a sen x + b cos x]

y’ = y + e ^x [b cos x – a sen x] -(2)

Nuevamente diferenciando obtenemos

y’ ‘ =y’ + e ^x [b cos x – a sen x – b sen x – a cos x]

y” = y’ + e ^x [b cos x – a sen x] – e ^x [a cos x + b sen x]

De la ecuación (1) y (2), obtenemos

y” = y’ + [y’ – y] – y

y” – 2y’ + 2y = 0

Pregunta 6. Forme la ecuación diferencial de la familia de círculos que tocan el eje y en el origen.

Solución:

Dado que la familia de círculos toca el eje y en el origen.

Entonces, el centro del círculo es (a, 0) y el radio a

Sea la ecuación de un círculo

(x – a) ² + y ² = a ²

= x2 + ^y2⁼ 2ax -(1)

Al diferenciar obtenemos

2x + 2yy’ = 2a

x + yy’ = un

Ahora sustituimos el valor de a en la ecuación (1), obtenemos

x2 + y2 ⁼² (x + yy’)x

x2 + ^y2^{= 2×2}⁺ 2xyy ‘

x2 + ^y2 – ^{2×2 –}^2xyy ‘

y2 ⁼ x2 ⁺ 2xyy’

Pregunta 7. Forme la ecuación diferencial de la familia de parábolas que tienen un vértice en el origen y un eje a lo largo del eje y positivo.

Solución:

Dado que la familia de parábolas tiene un vértice en el origen y un eje a lo largo del eje y positivo.

Entonces la ecuación de la parábola es:

x ² = 4ay -(1)

Al diferenciar obtenemos

2x = 4ay’ -(2)

Ahora dividimos la ecuación (2) por (1), tenemos

2x/ x ² = 4ay’ /4ay

2/x= y’ /y

y’x = 2y

y’x – 2y = 0

Pregunta 8. Forme la ecuación diferencial de la familia de elipses que tienen focos en el eje y y centro en el origen.

Solución:

Dado que la familia de elipses tiene facii o eje y y centro en el origen.

Entonces la ecuación de la parábola es

$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$

Al diferenciar obtenemos

$\frac{2x}{b^2}+\frac{2y}{a^2}y'=0$

$y'=\frac{-xb^2}{ya^2}$

$\frac{yy'}{x}=\frac{-b^2}{a^2}$

Nuevamente diferenciando obtenemos

$\frac{x[yy''+(y')^2]-yy'}{x^2}=0$

xyy” + x(y’) ² – yy’ = 0

Pregunta 9. Forme la ecuación diferencial de la familia de hipérbolas que tienen focos en el eje x y centro en el origen.

Solución:

Dado que la familia de hipérbolas tiene focos en el eje x y centro en el origen.

Entonces la ecuación de la hipérbola es

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Al diferenciar obtenemos

$\frac{2x}{a^2}+\frac{2y}{b^2}y'=0$

$y'=\frac{b^2}{a^2y}$

$\frac{yy'}{x}=\frac{b^2}{a^2}$

Nuevamente diferenciando obtenemos

$\frac{x[yy''+(y')^2]-yy'}{x^2}=0$

$y'\sqrt{9-x^2}-x=0$

Pregunta 10. Forme la ecuación diferencial de la familia de círculos que tienen un centro en el eje y y un radio de 3 unidades.

Solución:

Dado que el de círculos que tienen un centro en el eje y y un radio de 3 unidades.

Entonces el centro sea (0, k)

La ecuación general de la circunferencia es,

x ² + (y – k) ² = 3 ²

(y – k) ² = 9 – x ²

y-k = $\sqrt{9-x^2}$

k = $y-\sqrt{9-x^2}$

Al diferenciar obtenemos

$y'-\frac{1}{2\sqrt{9-x^2}}.(-2x)=0$

$y'+\frac{x}{\sqrt{9-x^2}}=0$

Cuadrando en ambos lados obtenemos

$(9-x^2)(y')^2+x^2=0$

Pregunta 11. ¿Cuál de las siguientes ecuaciones diferenciales tiene y = c ₁ e ^x + c ₂ e ^-x como solución general?

(A) 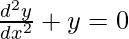$\frac{d^2y}{dx^2}+y=0$

(B) 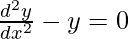$\frac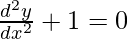{d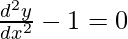^2y}{dx^2}-y=0$

(C) $\frac{d^2y}{dx^2}+1=0$

(D) $\frac{d^2y}{dx^2}-1=0$

Solución:

y = c ₁ e ^x + c ₂ e ^-x

Al diferenciar obtenemos

y’ = c ₁ e ^x – c ₂ e ^-x

Nuevamente diferenciando obtenemos

y” = c ₁ e ^x + c ₂ e ^-x

y” = y

y” – y = 0

Por lo tanto, la opción correcta es B

Pregunta 12. ¿Cuál de las siguientes ecuaciones diferenciales tiene y = x como una de sus soluciones particulares?

(A) 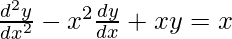$\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=x$

(B) 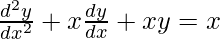$\frac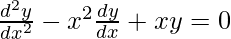{d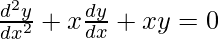^2y}{dx^2}+x\frac{dy}{dx}+xy=x$

(C) $\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=0$

(D) $\frac{d^2y}{dx^2}+x\frac{dy}{dx}+xy=0$

Solución:

y = x

Al diferenciar obtenemos

y’ = 1

Nuevamente diferenciando obtenemos

y” = 0

Ahora sustituya el valor de y, y’ e y” en cada opción para verificar la opción correcta

(A) $\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=x$

= 0 – x ² (1) + xx = x

0 ≠ x

(B) $\frac{d^2y}{dx^2}+x\frac{dy}{dx}+xy=x$

= 0 + x(1) + xx = x

= x + x ² ≠ x

(C) $\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=0$

= 0 – x2 ( ¹ ) + xx = 0

= 0 = 0

Por lo tanto, la opción correcta es C.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

En cada uno de los ejercicios 1 a 5, a partir de una ecuación diferencial que represente la familia de curvas dada eliminando las restricciones arbitrarias a y b.

Pregunta 1.

Pregunta 2.

Pregunta 3. y = ae 3x +be -2x

Pregunta 4. y = e 2x (a + bx)

Pregunta 5.

Pregunta 6. Forme la ecuación diferencial de la familia de círculos que tocan el eje y en el origen.

Pregunta 7. Forme la ecuación diferencial de la familia de parábolas que tienen un vértice en el origen y un eje a lo largo del eje y positivo.

Pregunta 8. Forme la ecuación diferencial de la familia de elipses que tienen focos en el eje y y centro en el origen.

Pregunta 9. Forme la ecuación diferencial de la familia de hipérbolas que tienen focos en el eje x y centro en el origen.

Pregunta 10. Forme la ecuación diferencial de la familia de círculos que tienen un centro en el eje y y un radio de 3 unidades.

Pregunta 11. ¿Cuál de las siguientes ecuaciones diferenciales tiene y = c 1 e x + c 2 e -x como solución general?

(A)

(B)

(C)

(D)

Pregunta 12. ¿Cuál de las siguientes ecuaciones diferenciales tiene y = x como una de sus soluciones particulares?

(A)

(B)

(C)

(D)

Deja una respuesta Cancelar la respuesta

Pregunta 1. $\frac{x}{a}+\frac{y}{b}=1$

Pregunta 2. $y^2=a(b^2-x^2)$

Pregunta 3. y = ae ^3x +be ^-2x

Pregunta 4. y = e ^2x (a + bx)

Pregunta 5. $y=e^x(a\cos x+b\sin x)$

Pregunta 11. ¿Cuál de las siguientes ecuaciones diferenciales tiene y = c ₁ e ^x + c ₂ e ^-x como solución general?

(A) $\frac{d^2y}{dx^2}+y=0$

(B) $\frac{d^2y}{dx^2}-y=0$

(C) $\frac{d^2y}{dx^2}+1=0$

(D) $\frac{d^2y}{dx^2}-1=0$

(A) $\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=x$

(B) $\frac{d^2y}{dx^2}+x\frac{dy}{dx}+xy=x$

(C) $\frac{d^2y}{dx^2}-x^2\frac{dy}{dx}+xy=0$

(D) $\frac{d^2y}{dx^2}+x\frac{dy}{dx}+xy=0$