Comprensión matemática de RNN y sus variantes.

Introducción:

Los expertos esperan que la Inteligencia Artificial (IA) trabaje para crear una vida mejor para vivir. Dicen que a medida que haya más poder de cómputo disponible en el futuro, es decir, más unidades de procesamiento gráfico, la IA hará más avances y será más productiva para los humanos. Hoy en día, se pueden ver muchas de estas aplicaciones impulsadas por IA como la lucha contra la trata de personas, asesores de atención médica, automóviles autónomos, detección y prevención de intrusiones, seguimiento y conteo de objetos, detección y reconocimiento de rostros, predicción de enfermedades y asistencia virtual para humanos. ayuda. Esta publicación en particular habla sobre RNN, sus variantes (LSTM, GRU) y las matemáticas detrás de él. RNN es un tipo de red neuronal que acepta entradas de longitud variable y produce salidas de longitud variable. Se utiliza para desarrollar diversas aplicaciones, como texto a voz, chatbots, modelado de lenguaje,

Tabla de contenidos:

• ¿Qué es RNN y en qué se diferencia de Feed Forward Neural Networks?
• Matemáticas detrás de RNN
• Variantes RNN (LSTM y GRU)
• Aplicaciones prácticas de RNN
• Nota final

Qué es RNN y en qué se diferencia de Feed Forward Neural Networks:

RNN es una red neuronal recurrente cuya salida actual no solo depende de su valor presente sino también de entradas pasadas, mientras que para la red feed-forward la salida actual solo depende de la entrada actual. Eche un vistazo al siguiente ejemplo para comprender RNN de una mejor manera.

Rahul pertenece al congreso.

Rahul es parte del equipo de cricket indio.

Si se le pregunta a alguien quién es Rahul, él / ella dirá que ambos Rahul son diferentes, es decir, uno es del congreso nacional indio y otro es del equipo de cricket indio. Ahora bien, si se le da la misma tarea a la máquina para dar la salida, no puede decir hasta que conozca el contexto completo, es decir, predecir la identidad de una sola palabra depende de conocer todo el contexto. Dichas tareas pueden implementarse mediante Bi-LSTM, que es una variante de RNN. RNN es adecuado para este tipo de trabajo gracias a su capacidad de aprender el contexto. Otras aplicaciones incluyen conversión de voz a texto, creación de asistencia virtual, pronóstico de acciones de series temporales, análisis sentimental, modelado de lenguaje y traducción automática. Por otro lado, una red neuronal feed-forward produce una salida que solo depende de la entrada actual. Ejemplos de esto son tareas de clasificación de imágenes, tarea de segmentación de imágenes o detección de objetos. Uno de estos tipos de red es una red neuronal convolucional (CNN). Recuerde que tanto RNN como CNN son modelos de aprendizaje profundo supervisados, es decir, necesitan etiquetas durante la fase de entrenamiento.

Matemáticas detrás de RNN

1.) Ecuación matemática de RNN

Para comprender las matemáticas detrás de RNN, eche un vistazo a la imagen a continuación.

Como se discutió dentro del primer encabezado, la producción depende de las entradas actuales y pasadas. Sea I ₁ la primera entrada cuya dimensión es n*1 donde n es la longitud del vocabulario. S ₀ sea el estado oculto de la primera célula RNN que tiene d neuronas. Para cada celda, el estado oculto de entrada debe ser uno anterior. Para la primera celda, inicialice S ₀ con ceros o algún número aleatorio porque no se ve ningún estado anterior. U sea otra array de dimensión d*n donde d es el número de neuronas en la primera celda RNN yn es el tamaño del vocabulario de entrada. W es otra array cuya dimensión esd* d b es el sesgo cuya dimensión es d*1 . Para encontrar la salida de la primera celda, se toma otra array V cuya dimensión es k*d donde c es un sesgo con dimensión k*1 .

Matemáticamente, las salidas de la primera celda RNN son las siguientes

S1= UI1+ WS0 + b
O1= VS1+c

En general,

Sn= UIn+ WSn-1 + b
On= VSn+c

Punto clave de la ecuación anterior

En general, la salida O _n depende de S _n y S _n depende de S _n-1 . Sn _-1 depende de Sn _-2 . El proceso continúa hasta que se logra S _{0 .} Esto demuestra claramente que la salida en el ^enésimo paso de tiempo depende de todas las entradas anteriores.

2.) Parámetros y Gradientes

Los parámetros en la RNN son U, V, b, c, W  se comparten entre todas las celdas de la RNN. El motivo de compartir es crear una función común que pueda aplicarse en todos los pasos de tiempo. Los parámetros se pueden aprender y son responsables de entrenar el modelo. En cada paso de tiempo, la pérdida se computa y se retropropaga a través del algoritmo de descenso de gradiente.

2.1) Gradiente de pérdida con respecto a V

El gradiente representa la pendiente de la tangente y apunta en la dirección de la mayor tasa de aumento de la función. Estamos interesados ​​en encontrar esa V donde la pérdida es mínima. De la pérdida, se entiende función de costo o error. En un sentido simple, la función de costo es la diferencia entre un valor real y un valor predicho. El movimiento se hace en dirección opuesta a la dirección del gradiente de la pérdida con respecto a V. Se obtiene matemáticamente un nuevo valor de V utilizando la fórmula matemática siguiente.

Donde d(L)/d(V) es la suma de todas las pérdidas obtenidas de los pasos de tiempo. Hay dos formas de actualizar los pesos. Una es calcular el gradiente del lote definido y luego actualizarlo (Mini Batch) o calcular por muestra y actualizar (Estocástico). Durante el cálculo de d(L)/d(V) , se aplica la regla de la string. Eche un vistazo a la siguiente figura para comprender el cálculo y la regla de la string.

2.2) Gradiente de pérdida con respecto a W

W se multiplica por S. Para calcular la derivada de la pérdida con respecto al peso en cualquier paso de tiempo, se aplica la regla de la string para tener en cuenta todo el camino para llegar a W desde S _n hasta S ₀ . _{Esto significa que debido a cualquiera de los Sn} incorrectos , W se ve afectado. En otras palabras, alguna información incorrecta provino de algún estado oculto que conduce a la pérdida. Matemáticamente, el peso se actualiza de la siguiente manera

El punto clave a recordar es que los gradientes y los pesos se actualizan en cada muestra o después de un lote. Esto depende del algoritmo que se elija, ya sea estocástico o mini-lote. Eche un vistazo a la siguiente captura de pantalla para visualizar el concepto de una manera más refinada.

Variantes RNN (LSTM y GRU)

De la discusión anterior, espero que las matemáticas detrás de RNN estén claras ahora. El principal inconveniente de RNN es que cualquiera que sea la longitud de la secuencia, la dimensión del vector de estado sigue siendo la misma. Tomando un caso en consideración, si la longitud de la secuencia de entrada es muy larga, se agrega nueva información al mismo vector de estado. Cuando uno alcanza el enésimo paso de tiempo que está muy lejos del primer paso de tiempo, la información es muy confusa. En tal posición, no está claro cuál fue la información proporcionada en el paso de tiempo 1 o 2. Es similar a una pizarra cuya dimensión es fija y uno sigue escribiendo en ella. En alguna posición, se vuelve muy desordenado. Ni siquiera se puede leer lo que está escrito a bordo. Para resolver tales problemas, se desarrollaron sus variantes denominadas LSTM y GRU. Funcionan según el principio de lectura, escritura y olvido selectivos.analogía con el vector de estado ) es igual, pero solo se escribe la información deseada en el paso de tiempo y se filtra la información innecesaria, lo que hace que la red neuronal secuencial sea adecuada para el entrenamiento con secuencias largas. Uno puede leer la diferencia entre LSTM y GRU desde aquí .

LSTM (Memoria a Largo Corto Plazo)  

Representación Matemática:

La estrategia seguida es escribir, leer y olvidar de forma selectiva.

Escritura selectiva:

En RNN,   S _{t – 1} se alimenta junto con x _t a una celda, mientras que en LSTM S _t-1 se transforma en h _t-1 usando otro vector O _t-1 . Este proceso se llama escritura selectiva . Las ecuaciones matemáticas para la escritura selectiva son las siguientes

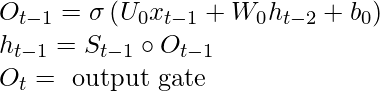
Lectura selectiva:

Echa un vistazo a la imagen de abajo para entender el concepto

h _t-1 se suma con x _t para producir s _t . Entonces producto de Hadamard de   (escrito s _tc en el diagrama) y se hace para obtener s _t . Esto se llama una puerta de entrada . En s _t sólo va la información selectiva y este proceso se llama lectura selectiva . Matemáticamente, las ecuaciones para la lectura selectiva son las siguientes

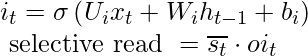
Olvido selectivo:

Echa un vistazo a la imagen de abajo para entender el concepto

s _t-1 es un producto hadamard con f _t y se llama olvido selectivo . La s _t global se obtiene de la adición de lectura selectiva y olvido selectivo. Vea el siguiente diagrama para entender la declaración anterior

Matemáticamente, las ecuaciones para el olvido selectivo son las siguientes

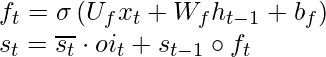
Nota: No hay una puerta de olvido en el caso de GRU (Unidad Recurrente Cerrada). Solo tiene puertas de entrada y salida.

Aplicaciones prácticas de RNN:

RNN encuentra su caso de uso en una conversión de voz a texto, creación de asistencia virtual, análisis sentimental, pronóstico de acciones de series temporales, traducción automática, modelado de lenguaje. Se están realizando más investigaciones sobre la creación de chatbots generativos utilizando RNN y sus variantes. Otras aplicaciones incluyen subtítulos de imágenes, generación de texto grande a partir de un párrafo pequeño y resumen de texto (una aplicación como Inshorts está usando esto). La composición musical y el análisis del centro de llamadas son otros dominios que utilizan RNN.

Nota final:

En pocas palabras, uno puede entender la diferencia entre RNN y la red neuronal de avance desde el párrafo inicial y luego profundizar en las matemáticas detrás de RNN. Al final, el artículo se completa explicando diferentes variantes de RNN y algunas aplicaciones prácticas de RNN. Para poder trabajar en aplicaciones de RNN, uno debe adquirir un sólido conocimiento en cálculo, especialmente en derivados, cómo funciona la regla de la string. Una vez que se estudia la teoría, se deben hacer algunos códigos sobre estos temas en su lenguaje de codificación favorito. Esto le proporcionará la ventaja.