Comprobar si el triángulo rectángulo es válido o no para lados grandes

Posted on by Rudeus Greyrat

Dados tres enteros a, b y c como tripletes. Compruebe si es posible hacer un triángulo en ángulo recto o no. Escriba Sí si es posible, de lo contrario No. 10 -18 <= a, b, c <= 10 18  
Ejemplos: 
 

Input: 3 4 5
Output: Yes
Explanation:
Since 3*3 + 4*4 = 5*5
Hence print "Yes"

Input: 8 5 13
Since 8 + 5 < 13 which violates the property of
triangle. Hence print "No"

Para que un triángulo rectángulo sea válido, debe satisfacer los siguientes criterios: 
 

  1. a, b y c deben ser mayores que 0. 
     
  2. La suma de cualquiera de los dos lados de un triángulo debe ser mayor que el tercer lado. 
     
  3. Teorema de Pitágoras, es decir, a 2 + b 2 = c 2 . 
     

Las dos primeras condiciones se pueden verificar fácilmente, pero para la tercera condición tenemos que cuidar el desbordamiento. Dado que a, b y c pueden ser grandes, no podemos compararlos directamente a menos que usemos la biblioteca python o BigInteger en Java. Para lenguajes como C y C++, tenemos que reducir la expresión en forma de fracción.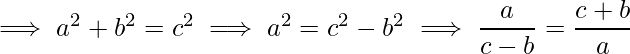 
\implies a^2 + b^2 = c^2 \implies a^2 = c^2 - b^2 \implies \dfrac{a}{c-b}=\dfrac{c+b}{a}
Antes de comparar la fracción necesitamos convertirlas en forma simplificada dividiendo el numerador y el denominador por mcd de ambos. Ahora compare tanto el numerador como el denominador de las fracciones de LHS y RHS de modo que si ambos se vuelven iguales, entonces significa el triángulo rectángulo válido; de lo contrario, no.
 

C++

// C++ program to check validity of triplets
#include <bits/stdc++.h>
using namespace std;
 
// Function to check pythagorean triplets
bool Triplets(long long a, long long b, long long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;
 
    vector<long long> vec{ a, b, c };
    sort(vec.begin(), vec.end());
 
    // Re-initialize a, b, c in ascending order
    a = vec[0], b = vec[1], c = vec[2];
 
    // Check validation of sides of triangle
    if (a + b <= c)
        return false;
 
    long long p1 = a, p2 = c - b;
 
    // Reduce fraction to simplified form
    long long div = __gcd(p1, p2);
    p1 /= div, p2 /= div;
 
    long long q1 = c + b, q2 = a;
 
    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div, q2 /= div;
 
    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}
 
// Function that will return 'Yes' or 'No'
// according to the correction of triplets
string checkTriplet(long long a, long long b, long long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}
 
// Driver code
int main()
{
    long long a = 4, b = 3, c = 5;
    cout << checkTriplet(a, b, c) << endl;
 
    a = 8, b = 13, c = 5;
    cout << checkTriplet(a, b, c) << endl;
 
    a = 1200000000000, b = 1600000000000,
    c = 2000000000000;
    cout << checkTriplet(a, b, c) << endl;
 
    return 0;
}

Java

// Java program to check validity of triplets
import java.util.*;
 
class GFG
{
     
// Function to check pythagorean triplets
static boolean Triplets(long a,
                        long b, long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;
 
    long []vec = { a, b, c };
    Arrays.sort(vec);
 
    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];
 
    // Check validation of sides of triangle
    if (a + b <= c)
        return false;
 
    long p1 = a, p2 = c - b;
 
    // Reduce fraction to simplified form
    long div = __gcd(p1, p2);
    p1 /= div; p2 /= div;
 
    long q1 = c + b, q2 = a;
 
    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;
 
    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}
 
// Function that will return 'Yes' or 'No'
// according to the correction of triplets
static String checkTriplet(long a,
                           long b, long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}
 
static long __gcd(long a, long b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
     
}
 
// Driver code
public static void main(String[] args)
{
    long a = 4, b = 3, c = 5;
    System.out.println(checkTriplet(a, b, c));
 
    a = 8; b = 13; c = 5;
    System.out.println(checkTriplet(a, b, c));
 
    a = 1200000000000L; b = 1600000000000L;
    c = 2000000000000L;
    System.out.println(checkTriplet(a, b, c));
}
}
 
// This code is contributed
// by Princi Singh

Python3

# Python3 program to check validity of triplets
def Triplets(a, b, c):
     
    if (a <= 0 or b <= 0 or c <= 0):
        return False
         
    vec = [ a, b, c ]
    vec.sort()
 
    # Re - initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2]
 
    # Check validation of sides of triangle
    if (a + b <= c):
        return False
 
    p1 = a; p2 = c - b
 
    # Reduce fraction to simplified form
    div = __gcd(p1, p2)
    p1 //= div
    p2 //= div
 
    q1 = c + b
    q2 = a
 
    # Reduce fraction to simplified form
    div = __gcd(q1, q2)
    q1 //= div
    q2 //= div
 
    # If fraction are equal return
    # 'true' else 'false'
    return (p1 == q1 and p2 == q2)
 
# Function that will return 'Yes' or 'No'
# according to the correction of triplets
def checkTriplet(a, b, c):
     
    if (Triplets(a, b, c)):
        return "Yes"
    else:
        return "No"
 
def __gcd(a, b):
    if (b == 0):
        return a
    return __gcd(b, a % b)
 
# Driver code
a = 4
b = 3
c = 5
print(checkTriplet(a, b, c))
 
a = 8
b = 13
c = 5
print(checkTriplet(a, b, c))
 
a = 1200000000000
b = 1600000000000
c = 2000000000000
print(checkTriplet(a, b, c))
 
# This code is contributed by ng24_7

C#

// C# program to check validity of triplets
using System;
     
class GFG
{
     
// Function to check pythagorean triplets
static Boolean Triplets(long a,
                        long b, long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;
 
    long []vec = { a, b, c };
    Array.Sort(vec);
 
    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];
 
    // Check validation of sides of triangle
    if (a + b <= c)
        return false;
 
    long p1 = a, p2 = c - b;
 
    // Reduce fraction to simplified form
    long div = __gcd(p1, p2);
    p1 /= div; p2 /= div;
 
    long q1 = c + b, q2 = a;
 
    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;
 
    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}
 
// Function that will return 'Yes' or 'No'
// according to the correction of triplets
static String checkTriplet(long a,
                        long b, long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}
 
static long __gcd(long a, long b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
     
}
 
// Driver code
public static void Main(String[] args)
{
    long a = 4, b = 3, c = 5;
    Console.WriteLine(checkTriplet(a, b, c));
 
    a = 8; b = 13; c = 5;
    Console.WriteLine(checkTriplet(a, b, c));
 
    a = 1200000000000L; b = 1600000000000L;
    c = 2000000000000L;
    Console.WriteLine(checkTriplet(a, b, c));
}
}
 
// This code has been contributed by 29AjayKumar

Javascript

<script>
 
// Javascript program to check validity of triplets
 
// Function to check pythagorean triplets
function Triplets(a, b, c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;
   
    let vec = [ a, b, c ];
    vec.sort();
   
    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];
   
    // Check validation of sides of triangle
    if (a + b <= c)
        return false;
   
    let p1 = a, p2 = c - b;
   
    // Reduce fraction to simplified form
    let div = __gcd(p1, p2);
    p1 /= div; p2 /= div;
   
    let q1 = c + b, q2 = a;
   
    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;
   
    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}
   
// Function that will return 'Yes' or 'No'
// according to the correction of triplets
function checkTriplet(a, b, c){
 
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}
   
function __gcd(a, b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
       
}
   
// driver program
    let a = 4, b = 3, c = 5;
    document.write(checkTriplet(a, b, c) + "<br/>");
   
    a = 8; b = 13; c = 5;
    document.write(checkTriplet(a, b, c)  + "<br/>");
   
    a = 1200000000000; b = 1600000000000;
    c = 2000000000000;
    document.write(checkTriplet(a, b, c)  + "<br/>");
 
// This code is contributed by sanjoy_62.
</script>

Producción: 
 

Yes
No
Yes

Complejidad temporal: O(log(M)) donde M es el valor máximo entre a, b y c. 
Espacio auxiliar: O(1)
Este artículo es una contribución de Shubham Bansal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *