Las técnicas básicas de construcción permiten construir bisectrices perpendiculares, bisectrices de ángulos, etc. Estas técnicas básicas se pueden utilizar para construcciones más complejas. Estas construcciones son muy esenciales para los diseñadores que diseñan edificios, carreteras, máquinas, etc. Por lo tanto, estas técnicas son muy útiles en la vida real. Como sugiere el nombre, los triángulos similares son aquellos triángulos que son similares en apariencia, ángulos y la proporción de sus lados. Pero si se da un triángulo y se pide hacer un triángulo semejante, ¿cómo se hará? ¿Existe la necesidad de construir todo el triángulo de nuevo? Para ello, se desarrollaron algunas técnicas de construcción para simplificar el proceso.
Triángulos similares
Los triángulos semejantes son triángulos que no son congruentes, pero son similares en naturaleza. Hay algunas condiciones que deben cumplirse cuando dos triángulos son similares.
Digamos que tenemos dos triángulos que son similares ΔABC y ΔXYZ. Los dos triángulos deben cumplir dos condiciones:
1. Los ángulos correspondientes de los triángulos deben ser iguales
∠A = ∠X, ∠B = ∠Y y ∠C = ∠Z
2. Los lados correspondientes de ambos triángulos deben estar en la misma proporción.
Construcción de Triángulos Similares
Esta construcción de triángulos semejantes implica dos casos:
- El triángulo a construir es más grande que el triángulo original.
- El triángulo a construir es más pequeño que el triángulo original.
Relación de escala: Definimos la relación de escala como la relación de los lados del triángulo construido con los lados del triángulo original.
Ejemplos de construcciones
Veamos la construcción en ambos casos a través de algunos ejemplos,
Pregunta 1: Construya un triángulo similar al triángulo ΔPQR con la relación de escala = 
Solución:
Sabemos que la razón de escala debe ser
, de los lados del triángulo original.
Pasos de construcción:
Paso 1. Dibujar un rayo QX que forme un ángulo agudo con QR en el lado opuesto a P.
Paso 2. Sobre el rayo QX, haz cuatro puntos Q 1 , Q 2 , Q 3 y Q 4 sobre QX de tal manera que QQ 1 = QQ 2 = QQ 3 = QQ 4 . Ahora, en este rayo, ubica el cuarto punto (el que sea mayor en la fracción
Paso 3. Ahora únase a Q 4 R y dibuje una línea desde Q 3 paralela a Q 4 R y deje que se cruce con QR en R’.
Paso 4. Dibujar una línea desde R’ que sea paralela a la línea RP. Que se crucen PQ y P’
ΔPQ’R’ es nuestro triángulo requerido.
Pregunta 2: Construya un triángulo similar al triángulo ΔPQR con la razón de escala = 
.
Solución:
Este es un ejemplo del segundo caso, la relación de escala viene dada por . Es decir, los lados del nuevo triángulo deben ser , de los lados del triángulo original. Los pasos en este caso son similares a los del caso anterior, pero con algunas modificaciones menores.
Pasos para la construcción:
Paso 1. Dibujar un rayo QX que forme un ángulo agudo con QR en el lado opuesto a P.
Paso 2. Sobre el rayo QX, haz cuatro puntos Q 1 , Q 2 , Q 3, Q 4, Q 5 sobre QX de tal manera que QQ 1 = QQ 2 = QQ 3 = QQ 4 = QQ 5 . Ahora, en este rayo, ubica el quinto punto, el que sea mayor en la fracción.
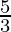
Paso 3. Una el 3er punto con R y dibuje una línea que sea paralela a Q 3 R a través del 5to punto, deje que se cruce con la línea extendida QR en R’.
Paso 4. Ahora, necesitamos dibujar la línea a través de R’ que, paralela a PR, debe intersecar la línea extendida de PQ y P’.
ΔP’QR’ es nuestro triángulo requerido.
Pregunta 3: Dibuja un triángulo de lados 10 cm, 11 cm y 8 cm. Luego dibuja un triángulo que sea similar a él con una relación de escala de 
.
Solución:
Pasos de la construcción:
Paso 1. Dibuja un triángulo de 10cm, 11cm y 8cm.
Sabemos que la razón de escala debe ser
, es decir, los lados del nuevo triángulo deben ser
Paso 2. Dibujar un rayo QX que forme un ángulo agudo con QR en el lado opuesto a P.
Paso 2. Sobre el rayo QX, haz tres puntos Q 1 , Q 2 , Q 3 sobre QX de tal manera que QQ 1 = QQ 2 = QQ 3 . Ahora, en este rayo, ubica el segundo punto (el que sea mayor en la fracción
Paso 3. Ahora únase a Q 3 R y dibuje una línea desde Q 2 paralela a Q 3 R y deje que se cruce con QR en R’.
Paso 4. Dibujar una línea desde R’ que sea paralela a la línea RP. Que se crucen PQ y P’
ΔPQ’R’ es nuestro triángulo requerido.
Pregunta 4: En el triángulo original de la pregunta anterior. Dibuja un triángulo que sea similar a él con una relación de escala de 
.
Solución:
Pasos de la construcción:
Paso 1. Dibuja un triángulo de 10cm, 11cm y 8cm.
Sabemos que la razón de escala debe ser
, es decir, los lados del nuevo triángulo deben ser
Paso 2. Dibujar un rayo QX que forme un ángulo agudo con QR en el lado opuesto a P.
Paso 3. Sobre el rayo QX, haz cuatro puntos Q 1 , Q 2 , Q 3, Q 4, Q 5 sobre QX de tal manera que QQ 1 = QQ 2 = QQ 3 = QQ 4 = QQ 5 . Ahora, en este rayo, ubica el quinto punto, el que sea mayor en la fracción.
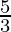
Paso 4. Una el 3er punto con R y dibuje una línea que sea paralela a Q 3 R a través del 5to punto, deje que se cruce con la línea extendida QR en R’.
Paso 5. Ahora, necesitamos dibujar la línea a través de R’ que, paralela a PR, debe intersecar la línea extendida de PQ y P’.
ΔP’QR’ es nuestro triángulo requerido.
Pregunta 5: Dibuja un triángulo de lados 4 cm, 5 cm y 6 cm. Luego dibuja un triángulo que sea similar a él con una relación de escala de .
Solución:
Pasos de la construcción:
Paso 1. Dibuja un triángulo de 4cm, 5cm y 6cm.
Sabemos que la razón de escala debe ser
Paso 2. Dibujar un rayo QX que forme un ángulo agudo con QR en el lado opuesto a P.
Paso 2. Sobre el rayo QX, haz tres puntos Q 1 , Q 2 , Q 3 sobre QX de tal manera que QQ 1 = QQ 2 = QQ 3 . Ahora, en este rayo, ubica el segundo punto (el que sea mayor en la fracción
Paso 3. Ahora únase a Q 3 R y dibuje una línea desde Q 2 paralela a Q 3 R y deje que se cruce con QR en R’.
Paso 4. Dibujar una línea desde R’ que sea paralela a la línea RP. Que se intersequen PQ y P’.
ΔPQ’R’ es nuestro triángulo requerido.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA