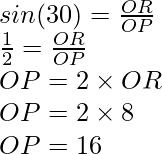Una línea puede pasar a través de un círculo de tres maneras: puede pasar a través de un solo punto del círculo, intersecarlo o puede pasar fuera de él. Una línea que pasa por un solo punto de un círculo se llama tangente. Cuando una recta corta a la circunferencia en dos puntos, la llamamos tangente. Arquitectos y diseñadores utilizan este concepto todos los días en su trabajo. En tales casos, se vuelve fundamental saber cómo construir una tangente a un círculo desde un punto que está fuera del círculo. Veamos ese procedimiento en detalle.
Tangente
La tangente de un círculo es una línea que corta al círculo en un solo punto. La siguiente figura muestra un ejemplo de una tangente que pasa por un círculo. El punto en el que la tangente corta a la circunferencia se llama punto de contacto. Observe que la tangente también es perpendicular a la línea que une el punto de contacto con el círculo.

Nota: Las líneas que intersecan círculos en dos puntos se llaman secantes.
Construcción de Tangente
Se pueden dibujar dos tangentes desde cualquier punto fuera del círculo. Nuestro objetivo es aprender a construir una sola tangente desde cualquier punto dado fuera del círculo. La otra tangente se puede dibujar de manera similar.
Pasos de construcción:
Nos dan una circunferencia de centro O con radio “r” y un punto A fuera de la circunferencia. Veamos cómo construir una tangente desde el punto A hasta el círculo.
Paso 1. Dibuja un círculo con radio r y llamemos a su centro O. Dibuja un punto A fuera del círculo.

Paso 2. Únete a OA y biséctalo. Llamaremos a su punto medio M.

Paso 3. Ahora con M como centro y radio MA. Dibuja un círculo que interseque el círculo dado en los puntos B y C.

Paso 4. Únete a AB y AC. Son nuestras tangentes dadas.

Problemas de muestra
Pregunta 1: Dibujar una tangente desde un punto P que está a 10 cm del centro O del círculo de 5 cm de radio.
Solución:
Circunferencia de centro O de radio “5cm” y punto P fuera de la circunferencia.
Paso 1. Dibuja un círculo con un radio de 5 cm y llamemos a su centro O. Dibuja un punto A que esté a 10 cm del centro fuera del círculo.
Paso 2. Únete a OP y biséctalo. Llamaremos a su punto medio M.
Paso 3. Ahora con M como centro y radio MP. Dibuja un círculo que interseque al círculo dado en los puntos Q y R.
Paso 4. Únete a PQ y PR. Son nuestras tangentes dadas.
Pregunta 2: Dibujar una tangente desde un punto P que está a 6 cm del centro O del círculo de radio 3 cm.
Solución:
Circunferencia de centro O de radio “3cm” y punto P fuera de la circunferencia.
Paso 1. Dibuja un círculo con un radio de 3 cm y llamemos a su centro O. Dibuja un punto A que esté a 6 cm del centro fuera del círculo.
Paso 2. Únete a OP y biséctalo. Llamaremos a su punto medio M.
Paso 3. Ahora con M como centro y radio MP. Dibuja un círculo que interseque al círculo dado en los puntos Q y R.
Paso 4. Únete a PQ y PR. Son nuestras tangentes dadas.
Pregunta 3: ¿Cuántas tangentes paralelas son posibles en un círculo?
Responder:
Hay como máximo dos posibles tangentes paralelas en un círculo. Se encuentran en puntos diametralmente opuestos.
Pregunta 4: Dibujar una tangente desde un punto P que está a 15 cm del centro O del círculo de 5 cm de radio.
Solución:
Circunferencia de centro O de radio “15cm” y punto P fuera de la circunferencia.
Paso 1. Dibuja un círculo con un radio de 5 cm y llamemos a su centro O. Dibuja un punto A que esté a 15 cm del centro fuera del círculo.
Paso 2. Únete a OP y biséctalo. Llamaremos a su punto medio M.
Paso 3. Ahora con M como centro y radio MP. Dibuja un círculo que interseque al círculo dado en los puntos Q y R.
Paso 4. Únete a PQ y PR. Son nuestras tangentes dadas.
Pregunta 5: Dibujar tangentes desde un punto P inclinado 30° desde la línea que une el punto y el centro del círculo de radio 8cm.
Solución:
Circunferencia de centro O de radio “8cm” y punto P fuera de la circunferencia.
Sabemos que las tangentes están inclinadas 30°. Digamos que se cruzan con el círculo en R y Q. Forma un triángulo OPR. Necesitamos saber la longitud de OP. También sabemos que OR es perpendicular a PR. Por lo tanto, es un triángulo rectángulo y podemos usar fórmulas trigonométricas para averiguar OP.
Por lo tanto, OP es de 16 cm. Ahora podemos construir una tangente.
Paso 1. Dibuja un círculo con un radio de 8 cm y llamemos a su centro O. Dibuja un punto P que está a 16 cm del centro fuera del círculo.
Paso 2. Únete a OP y biséctalo. Llamaremos a su punto medio M.
Paso 3. Ahora con M como centro y radio MP. Dibuja un círculo que interseque al círculo dado en los puntos Q y R.
Paso 4. Únete a PQ y PR. Son nuestras tangentes dadas.
Pregunta 6: Dibujar una tangente desde un punto P que está a 11 cm del centro O del círculo de radio 6 cm.
Solución:
Circunferencia de centro O de radio “6cm” y punto P fuera de la circunferencia.
Paso 1. Dibuja un círculo con un radio de 6 cm y llamemos a su centro O. Dibuja un punto A que esté a 11 cm del centro fuera del círculo.
Paso 2. Únete a OP y biséctalo. Llamaremos a su punto medio M.
Paso 3. Ahora con M como centro y radio MP. Dibuja un círculo que interseque al círculo dado en los puntos Q y R.
Paso 4. Únete a PQ y PR. Son nuestras tangentes dadas.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA