Cuente el número total de triángulos después de la enésima operación

Dado un triángulo equilátero, la tarea es calcular el número total de triángulos después de realizar la siguiente operación N veces. 
Para cada operación, los triángulos sin color se toman y se dividen en 4 triángulos equiláteros iguales. Cada triángulo invertido formado está coloreado. Consulte la siguiente figura para obtener más detalles.
Para N=1 el triángulo formado es:
 

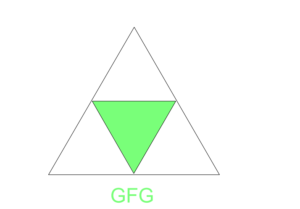
Para N=2 el triángulo formado es:
 

Ejemplos: 
 

Entrada: N = 10 
Salida: 118097
Entrada: N = 2 
Salida: 17 
 

Acercarse: 
 

• En cada operación se forman 3 triángulos sin color, 1 triángulo de color y el propio triángulo
• Al escribir la declaración anterior matemáticamente; recuento de triángulos en el N-ésimo movimiento = 3 * recuento de triángulos en el (N-1)-ésimo movimiento + 2
• Por lo tanto, inicializando una variable curr = 1 y tri_count = 0
• A continuación, se itera un ciclo de 1 a N
• Para cada iteración, se realiza la operación mencionada anteriormente.
• Finalmente, se devuelve el tri_count

A continuación se muestra la implementación del enfoque anterior: 
 

#include <bits/stdc++.h>
using namespace std;
// function to return the
// total no.of Triangles
int CountTriangles(int n)
{
    int curr = 1;
    int Tri_count = 0;
    for (int i = 1; i <= n; i++) {
        // For every subtriangle formed
        // there are possibilities of
        // generating (curr*3)+2
 
        Tri_count = (curr * 3) + 2;
        // Changing the curr value to Tri_count
        curr = Tri_count;
    }
    return Tri_count;
}
 
// driver code
int main()
{
    int n = 10;
    cout << CountTriangles(n);
    return 0;
}

class Gfg {
    // Method to return the
    // total no.of Triangles
    public static int CountTriangles(int n)
    {
        int curr = 1;
        int Tri_count = 0;
        for (int i = 1; i <= n; i++) {
            // For every subtriangle formed
            // there are possibilities of
            // generating (curr*3)+2
 
            Tri_count = (curr * 3) + 2;
            // Changing the curr value to Tri_count
            curr = Tri_count;
        }
        return Tri_count;
    }
 
    // driver code
    public static void main(String[] args)
    {
        int n = 10;
        System.out.println(CountTriangles(n));
    }
}

# Function to return the
# total no.of Triangles
def countTriangles(n):
     
    curr = 1
    Tri_count = 0
    for i in range(1, n + 1):
             
        # For every subtriangle formed
        # there are possibilities of
        # generating (curr * 3)+2
        Tri_count = (curr * 3) + 2
        # Changing the curr value to Tri_count
        curr = Tri_count
    return Tri_count
     
n = 10
print(countTriangles(n))

using System;
 
class Gfg
{
    // Method to return the
    // total no.of Triangles
    public static int CountTriangles(int n)
    {
        int curr = 1;
        int Tri_count = 0;
        for (int i = 1; i <= n; i++)
        {
            // For every subtriangle formed
            // there are possibilities of
            // generating (curr*3)+2
            Tri_count = (curr * 3) + 2;
             
            // Changing the curr value to Tri_count
            curr = Tri_count;
        }
        return Tri_count;
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        int n = 10;
        Console.WriteLine(CountTriangles(n));
    }
}
 
// This code is contributed by 29AjayKumar

<script>
    // Method to return the
    // total no.of Triangles
    function CountTriangles(n)
    {
        var curr = 1;
        var Tri_count = 0;
        for (i = 1; i <= n; i++)
        {
         
            // For every subtriangle formed
            // there are possibilities of
            // generating (curr*3)+2
 
            Tri_count = (curr * 3) + 2;
            // Changing the curr value to Tri_count
            curr = Tri_count;
        }
        return Tri_count;
    }
 
    // driver code
        var n = 10;
        document.write(CountTriangles(n));
 
// This code is contributed by aashish1995
</script>

118097

Complejidad de tiempo: O(n)

Espacio Auxiliar: O(1)