DeepPose fue propuesto por investigadores de Google para Pose Estimation en la conferencia Computer Vision and Pattern Recognition de 2014. Trabajan en la formulación del problema de estimación de pose como un problema de regresión basado en DNN hacia las articulaciones del cuerpo. Presentan una cascada de regresores DNN que dieron como resultado estimaciones de pose de alta precisión.
Arquitectura:
Pose de vectores:
- Para expresar el cuerpo humano en forma de pose, los autores de este artículo codifican la ubicación de todas las k partes del cuerpo en articulaciones llamadas vectores de pose definidos de la siguiente manera
![]()
- donde yi representa las coordenadas x, y de la ubicación de la i -ésima articulación del cuerpo.
- La imagen se representa en forma de (x, y), donde x son los datos de la imagen y y son los datos del vector de pose real del suelo.
- Dado que las coordenadas descritas aquí son coordenadas de imagen absolutas en tamaño de imagen completo. Si cambiamos el tamaño de la imagen, eso puede causar el problema. Por lo tanto, normalizamos las coordenadas con un cuadro delimitador b que delimita el cuerpo humano o algunas partes del mismo. Estos cuadros están representados por b = (b c , b h , b w, ) donde b c es el centro del cuadro delimitador, b h es la altura y b w es el ancho del delimitador.
- Normalizamos las coordenadas de ubicación usando la siguiente fórmula.
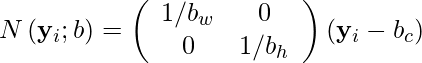
- Finalmente obtenemos las coordenadas del vector Pose normalizadas.
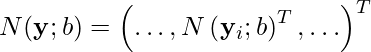
Arquitectura CNN
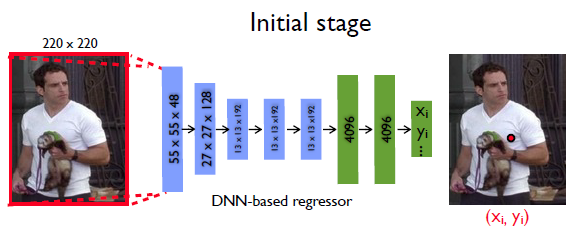
- Los autores de este artículo utilizan AlexNet como su arquitectura CNN porque ha mostrado excelentes resultados en la tarea de localización de imágenes.
![]()
- donde theta representa los parámetros entrenables (pesos y sesgos), shi representa la arquitectura neuronal aplicada al vector de pose normalizado N(x). La salida predicha y * puede obtenerse mediante la desnormalización de la salida (N- 1 ).
- Esta arquitectura de red neuronal toma una imagen de tamaño 220 × 220 y aplica un paso de 4 .
- La arquitectura CNN contiene 7 capas que se pueden enumerar como: C (55 × 55 × 96) — LRN — P — C (27 × 27 × 256) — LRN — P — C (13 × 13 × 384) — C (13) ×13×384) — C(13×13×256) — P — F(4096) — F(4096)
- donde C es la capa de convolución que utiliza ReLU como función de activación para introducir la no linealidad en el modelo, LRN es la normalización de la respuesta local, P es la capa de agrupación y F es la capa completamente conectada.
- La última capa de arquitectura genera 2k coordenadas conjuntas.
- El número total de parámetros es de 40 millones.
- La arquitectura utiliza la función de pérdida L2 para minimizar la distancia entre las coordenadas predichas y la función de pérdida de verdad del terreno.
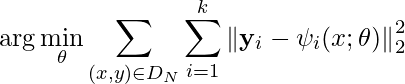
- donde k es el número de articulaciones en la imagen
regresor DNN:
- No es fácil aumentar el tamaño de entrada para tener una estimación de pose más precisa, ya que esto aumentará la ya gran cantidad de parámetros. Por lo tanto, se propone una cascada de regresores de pose para refinar la estimación de pose.
- Ahora, representamos la primera etapa con la siguiente ecuación
![]()
- donde b 0 representa la imagen completa o cuadro delimitador obtenido por un detector de personas.
- Ahora para las siguientes etapas s>= 2:
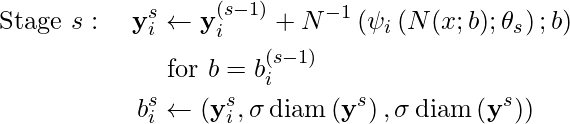
- yy _
- la cascada del regresor DNN mejoró la precisión, como podemos notar en las siguientes imágenes.

Métrica:
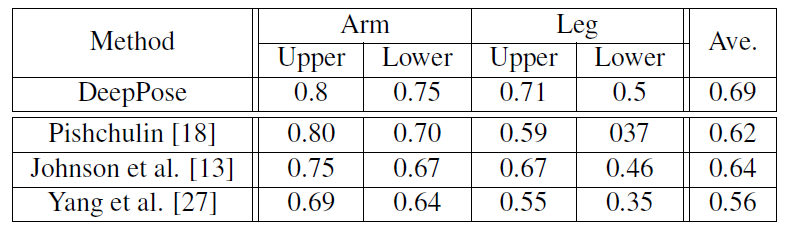
- Porcentaje de piezas correctas (PCP) : mide la tasa de detección de las extremidades, donde una extremidad se considera detectada si la distancia entre las dos ubicaciones previstas de las articulaciones y las ubicaciones reales de las articulaciones de las extremidades es como máximo la mitad de la longitud de la extremidad. Sin embargo, tiene inconvenientes como penalizar extremidades más cortas y más difíciles de detectar.
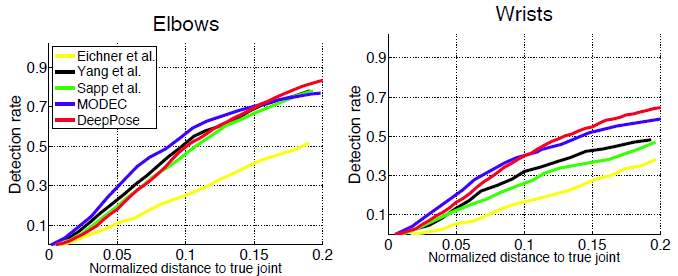
- Porcentaje de articulaciones detectadas (PDJ)
Resultados:
- Conjunto de datos Framed Label In Cinema (FLIC): este conjunto de datos contiene 4000 imágenes de trenes con 1000 imágenes de prueba de películas de Hollywood con diferentes poses y ropa. Para cada ser humano etiquetado, se etiquetan 10 articulaciones de la parte superior del cuerpo.

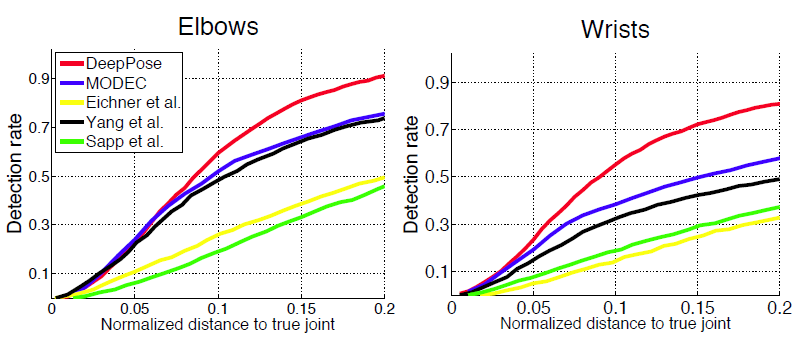
- Conjunto de datos deportivos de Leeds (LSP): este conjunto de datos contiene

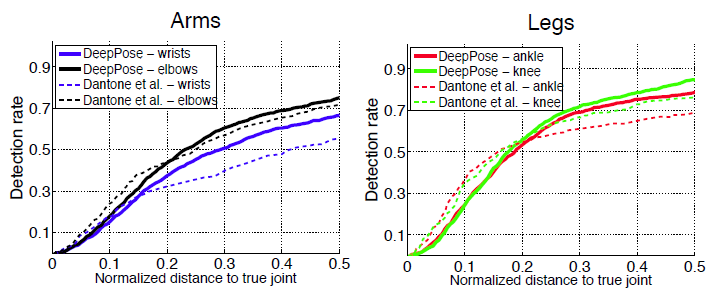
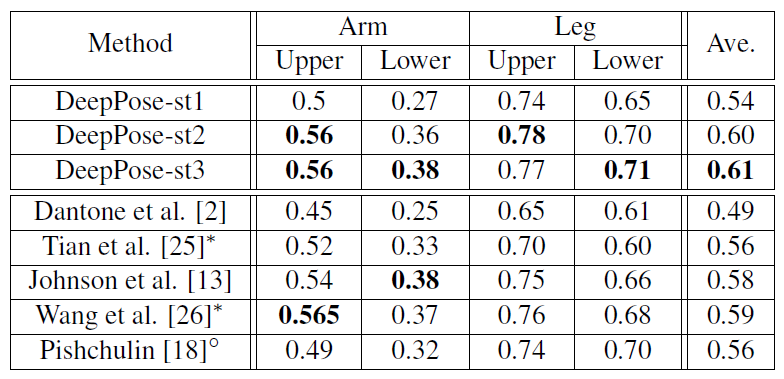
Referencias: