La trigonometría es la relación entre los ángulos y los lados de un triángulo rectángulo. En un triángulo rectángulo, hay 3 ángulos de los cuales un ángulo es un ángulo recto (90°) y los otros dos ángulos son ángulos agudos y hay 3 lados. El lado opuesto al ángulo recto se llama hipotenusa. Hay 6 razones entre estos lados basadas en el ángulo entre ellos y se llaman razones trigonométricas.
Las 6 razones trigonométricas son:
- Seno (pecado)
- Coseno (cos)
- Tangente (bronceado)
- Cosecante (cosec)
- secante (seg)
- Cotangente (cuna)
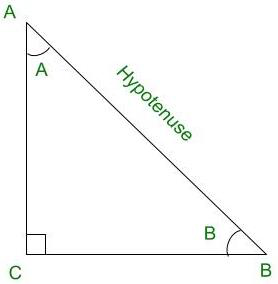
Triángulo rectángulo CBA
Seno (pecado):
El seno de un ángulo se define por la relación entre las longitudes de los lados opuestos al ángulo y la hipotenusa. Para el triángulo anterior, sen A = BC/AB
Coseno (cos):
El coseno de un ángulo se define por la relación entre las longitudes de los lados adyacentes al ángulo y la hipotenusa. Para el triángulo anterior, cos A = AC/AB
Tangente (bronceado):
La tangente de un ángulo se define por la relación entre la longitud de los lados opuestos al ángulo y el lado adyacente al ángulo. Para el triángulo anterior, tan A = BC/AC
Cosecante (cosec):
La cosecante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado opuesto al ángulo. Para el triángulo anterior, cosec A = AB/BC
Secante (s):
La secante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado y el lado adyacente al ángulo Para el triángulo anterior, sec A = AB/AC
Cotangente (cot):
La cotangente de un ángulo se define como la razón entre la longitud de los lados adyacentes al ángulo y el lado opuesto al ángulo. Para el triángulo anterior, cot A = AC/BC
Demostrar que: {cos (X – Y)}/{cosX.cosY } = 1 + tanX.tanY

Triángulo rectángulo XZY
LHS = {cos (X – Y)}/{cosX.cosY}
Sabemos que, cos (A – B) = cosA.cosB + sinA.sinB
⇒ LHS = (cosX.cosY + sinX.sinY) / (cosX.cosY)
= (cosX.cosY/cosX.cosY) + (senX.senY)/(cosX.cosY)
= 1 + (senX.senY)/(cosX.cosY)
Como tanA = senA/cosA,
⇒ LHS = 1 + tanX.tanY ………………..( 1 )
RHS = 1 + tanX.tanY ………………..( 2 )
De (1) y (2)
LHS = RHS
⇒ {cos (X – Y)}/{cosX.cosY} = 1 + tanX.tanY
Por lo tanto probado.
Preguntas similares
Pregunta 1: Prueba la identidad dada. {cos (X + Y)}/{cosX.cosY} = 1 – tanX.tanY
Prueba:
LHS = {cos (X + Y)}/{cosX.cosY}
Sabemos que, cos (A + B) = cosA.cosB – sinA.sinB
⇒ LHS = (cosX.cosY – senX.senY)/(cosX.cosY)
= ( cosX.cosY / cosX.cosY ) – ( senX.senY ) / ( cosX.cosY )
= 1 – ( senX.senY ) / ( cosX.cosY )
Como tanA = senA / cosA,
⇒ LHS = 1 – tanX.tanY ………………..( 1 )
RHS = 1 – tanX.tanY ………………..( 2 )
De ( 1 ) y ( 2 )
LHS = RHS
⇒ {cos (X + Y)}/{cosX.cosY} = 1 – tanX.tanY
Por lo tanto probado.
Pregunta 2: Prueba la identidad dada. {sen (X – Y)}/{cosX.cosY } = tanX – tanY
Prueba:
LHS = {sen (X – Y)}/{cosX.cosY}
Sabemos que, sin (A – B) = sinA.cosB – cosA.sinB
⇒ LHS = (senX.cosY – cosX.senY)/(cosX.cosY)
= (senX.cosY / cosX.cosY) – (cosX.senY) / (cosX.cosY)
Como tanA = senA / cosA,
⇒ LHS = tanX – tanY ………………..( 1 )
RHS = tanX – tanY ………………..( 2 )
De (1) y (2)
LHS = RHS
⇒ {sen (X – Y)}/{cosX.cosY} = tanX – tanY
Por lo tanto probado.
Pregunta 3: Prueba la identidad dada. {sen (X + Y)}/{cosX.cosY} = tanX + tanY
Prueba:
LHS = {sen (X + Y)}/{cosX.cosY}
Sabemos que, sin (A + B) = sinA.cosB + cosA.sinB
⇒ LHS = (senX.cosY + cosX.senY) / (cosX.cosY)
= (senX.cosY / cosX.cosY) + (cosX.senY) / (cosX.cosY)
Como tanA = senA / cosA,
⇒ LHS = tanX + tanY ………………..( 1 )
RHS = tanX + tanY ………………..( 2 )
De (1) y (2)
LHS = RHS
⇒ {sen (X + Y)}/{cosX.cosY} = tanX + tanY
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por rajsanghavi9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA