Desigualdades en un Triángulo

Sabemos que una figura cerrada formada por tres lados se conoce como triángulo. Un triángulo tiene tres lados, tres vértices y tres ángulos. La suma de los ángulos de cualquier tipo de Triángulo siempre da un total de 180°. Hay tres tipos de triángulos: Triángulo equilátero (todos los lados y todos los ángulos son siempre iguales (60°)), Triángulo isósceles (aquí, dos lados y dos ángulos se consideran iguales), Triángulo escaleno (estas son las formas más generalizadas de triángulos ya que ninguno de los lados o ángulos se consideran iguales). Si la altura del triángulo se representa como H y la base se representa como B, entonces el 

El área del triángulo se muestra como 

En la figura anterior, ABC es un triángulo. AB, BC y AC son los tres lados de un triángulo, ∠A, ∠B y ∠C son los ángulos de este triángulo. Estudiemos algunas propiedades y desigualdades de los triángulos. 

Triángulo isósceles

Un triángulo en el que dos lados son iguales se llama triángulo isósceles. Entonces, tiene AB = AC, la palabra ‘Isósceles’ significa «Dos patas», por lo tanto, en un Triángulo también, cuando dos patas/dos lados son iguales, el triángulo se conoce como Triángulo Isósceles. De los triángulos isósceles bien conocidos, uno es el ‘triángulo isósceles recto’ donde un ángulo es de 90° y los dos lados (base y perpendicular) son iguales.

Ejemplo de Triángulo Isósceles:

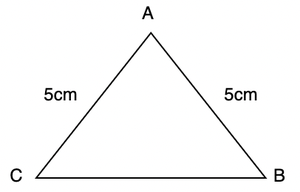
Teorema: Los ángulos opuestos a lados iguales en un triángulo isósceles son iguales. 

Prueba: 

Necesitamos demostrar que ∠B y ∠C son iguales. Dibujemos la bisectriz de ∠A y la unamos a BC. 

En el triángulo BAD y CAD, 

AB = CA, 

∠MALO =∠CAD

DA = DA

Entonces, los dos triángulos son congruentes. 

Entonces, ∠B y ∠C son ángulos correspondientes de triángulos congruentes. Por lo tanto, son iguales. 

¿Es también cierto el inverso de este teorema? Si dos ángulos de un triángulo son iguales, ¿eso significa que los lados opuestos a ellos también son iguales? 

Sí, lo contrario también es cierto, este teorema se puede probar de manera similar, usando la regla de congruencia ASA. 

Resolvamos algunos problemas relacionados con la prueba con respecto a estas propiedades:

Pregunta 1: E y F son respectivamente los puntos medios de los lados iguales AB y AC de Δ ABC (ver figura). Demuestre que BF = CE.

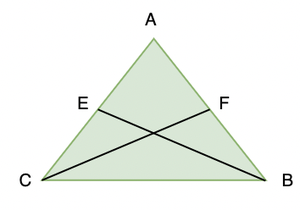
Solución:

En Δ ABF y Δ ACE,

AB = AC (Dado)

∠ A = ∠ A (Común)

AF = AE (Mitades de lados iguales)

Entonces, Δ ABF ≅ Δ ACE (regla SAS)

Por lo tanto, BF = CE (CPCT)

Pregunta 2: En un triángulo isósceles ABC con AB = AC, D y E son puntos en BC tales que BE = CD. Demuestre que AD = AE.

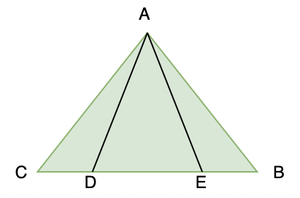
Solución:

En Δ ABD y Δ ACE,

AB = AC (Dado)

∠ B = ∠ C (Ángulos opuestos a lados iguales) 

Además, BE = CD

Entonces, BE – DE = CD – DE

Es decir, BD = CE

Entonces, Δ ABD ≅ Δ ACE (usando la regla SAS)

Esto da AD = AE

Por lo tanto, Probado. 

Triángulos equiláteros

Los triángulos en los que los tres lados son iguales se llaman triángulos equiláteros. Los tres ángulos de un Triángulo Equilátero son iguales y como la suma de todos los ángulos es 180°, cada ángulo es 60° respectivamente. Es importante tener en cuenta que todos los triángulos equiláteros son siempre similares entre sí.

Teorema: Si ABC es un triángulo equilátero y P es un punto sobre el arco BC de la circuncircunferencia del triángulo ABC, entonces; PA = PB + PC

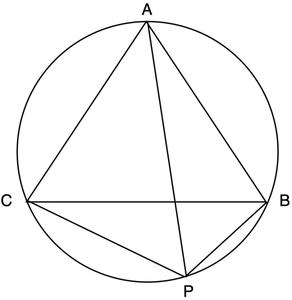
Prueba:

Para un cuadrilátero cíclico ABPC, tenemos;

PA.BC=PB.AC+PC.AB

Para un triángulo equilátero ABC,

AB = BC = CA

Entonces, PA.AB = PB.AB+PC.AB

Tomando AB como común;

PA.AB = AB(PB+PC)

PA = PB + PC

Por lo tanto, probado.

Ordenar lados y ángulos de triángulos

Podemos ordenar los lados en orden creciente de longitud si nos dan los ángulos. De manera similar, los ángulos del triángulo se pueden ordenar. Las propiedades de que el lado más grande es directamente opuesto al ángulo más grande y así sucesivamente vienen a nuestro rescate.

Pregunta: En el triángulo ABC que se muestra a continuación, ordene los lados del más corto al más largo usando los ángulos dados. 

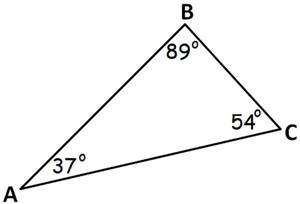
Responder: 

En cualquier triángulo, el ángulo más pequeño siempre es opuesto al lado más corto y el ángulo más grande siempre es opuesto al lado más largo y viceversa. En el triángulo ABC dado arriba, debido a que el ángulo A es el ángulo más pequeño, el lado BC debe ser el lado más corto. Y también, debido a que el ángulo B es el ángulo más grande, el lado AC debe ser el lado más largo. Pongamos todo junto. Por lo tanto, el orden de los tres lados de menor a mayor es el lado BC, el lado AB y el lado AC.

Teorema de la desigualdad del triángulo

Hasta ahora, nos hemos centrado en la igualdad de lados y ángulos de un triángulo o triángulos. A veces, nos encontramos con objetos desiguales, necesitamos compararlos.

Teorema 1: Si dos lados de un triángulo son desiguales, entonces el ángulo opuesto al lado mayor es mayor. 

Teorema 2: En cualquier triángulo, el lado opuesto al ángulo mayor (mayor) es más largo. Es lo contrario del Teorema 1 mencionado anteriormente.

Teorema 3: La suma de dos lados cualesquiera de un triángulo siempre es mayor que el tercer lado.

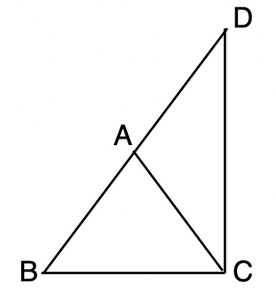
Prueba:

Observe que el lado BA de Δ ABC se ha producido hasta un punto D tal que AD = AC. Ahora, dado que ∠BCD > ∠BDC. 

Por las propiedades mencionadas anteriormente, podemos concluir que BD > BC. 

Sabemos que, BD = BA + AD

Entonces, BA + AD > BC 

= BA + AC > BC 

Entonces, esta suma probada de dos lados del triángulo siempre es mayor que el otro lado.  

Pregunta: D es un punto del lado BC del triángulo ABC tal que AD = DC. Demuestre que AB > BD. 

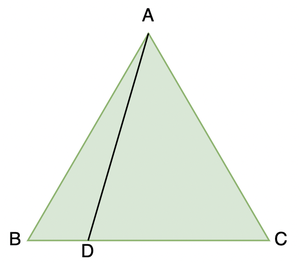
Solución :

En el triángulo DAC, 

DA = CA, 

∠ADC = ∠ACD (Ángulos opuestos a lados iguales)

∠ ADC es un ángulo exterior para ΔABD.

∠ ADC > ∠ ABD

∠ ACD > ∠ ABD

∠ ACB > ∠ ABC

AB > AC (Lado opuesto al ángulo mayor en Δ ABC)

AB > AD (AD = AC)