Diagonalización de arrays – Barcelona Geeks

Requisito previo: valores propios y vectores propios

Sean A y B dos arrays de orden n. B puede considerarse similar a A si existe una array invertible P tal que B=P^{-1} AP Esto se conoce como Transformación de similitud de arrays.

La diagonalización de una array se define como el proceso de reducir cualquier array A a su forma diagonal D. Según la transformación de similitud, si la array A está relacionada con D, entonces

$D = P ^{-1} AP$ y la array A se reduce a la array diagonal D a través de otra array P. Donde P es una array modal)

Array modal: Es una array (nxn) que consta de vectores propios. Generalmente se usa en el proceso de diagonalización y transformación de similitud.

En palabras más simples, es el proceso de tomar una array cuadrada y convertirla en un tipo especial de array llamada array diagonal.

Pasos involucrados:

Paso 1: Inicializar la array diagonal D como:

$D=\left[\begin{array}{ccc} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]$

donde λ _{1, λ2, λ3 ->} valores propios

Paso 2: Encuentre los valores propios usando la ecuación dada a continuación.

$\operatorname{det}(A-\lambda I)=0$

donde, A -> dada array cuadrada de 3×3. I -> array identidad de tamaño 3×3. λ -> valor propio.

Paso 3: Calcule los vectores propios correspondientes utilizando la ecuación que se proporciona a continuación.
$\begin{array}{l} A t, \lambda=i \\ {[A-\lambda I] X_{i}=0} \end{array}$
donde, λ _{i ->} valor propio. X _{i ->} vector propio correspondiente.

Paso 4: Cree la array modal P.

$P=\left[X_{0} X_{1} . . X_{n}\right]$

Aquí, todos los vectores propios hasta X _i se han llenado por columnas en la array P.

Paso 5: Encuentra P ^-1 y luego usa la ecuación dada a continuación para encontrar la array diagonal D.

$D=P^{-1} A P$

Problema de ejemplo:

Declaración del problema: suponga que una array cuadrada A de 3 × 3 tiene los siguientes valores:

$A=\left[\begin{array}{ccc} 1 & 0 & -1 \\ 1 & 2 & 1 \\ 2 & 2 & 3 \end{array}\right]$

Encuentre la array diagonal D de A usando la diagonalización de la array. [ D = P ^-1 AP ]

Solución:
Paso 1: Inicializar D como:

$D=\left[\begin{array}{ccc} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]$

Paso 2: Encuentra los valores propios. (o posibles valores de λ)

$\operatorname{det}(A-\lambda I)=0$

$\begin{array}{l} \Longrightarrow \operatorname{det}(A-\lambda I)=\operatorname{det}\left(\left[\begin{array}{ccc} 1-\lambda & 0 & -1 \\ 1 & 2-\lambda & 1 \\ 2 & 2 & 3-\lambda \end{array}\right]\right)=0 \\ \Longrightarrow\left(\lambda^{3}-6 \lambda^{2}+11 \lambda-6\right)=0 & \\ \Longrightarrow(\lambda-1)(\lambda-2)(\lambda-3)=0 \\ \Longrightarrow & \lambda=1,2,3 \end{array}$

Paso 3: Encuentre los vectores propios X ₁ , X ₂ , X ₃ correspondientes a los valores propios λ = 1,2,3.

$At $\lambda=1$ A - $(1) I$ $X_{1}=0$ $\Longrightarrow\left[\begin{array}{ccc}1-1 & 0 & -1 \\ 1 & 2-1 & 1 \\ 2 & 2 & 3-1\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$ $\Longrightarrow\left[\begin{array}{ccc}0 & 0 & -1 \\ 1 & 1 & 1 \\ 2 & 2 & 2\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$ On solving, we get the following equations: $x_{3}=0\left(x_{1}\right)$ $x_{1}+x_{2}=0 \Longrightarrow x_{2}=-x_{1}$ $\therefore X_{1}=\left[\begin{array}{c}x_{1} \\ -x_{1} \\ 0\left(x_{1}\right)\end{array}\right]$ $\Longrightarrow X_{1}=\left[\begin{array}{c}1 \\ -1 \\ 0\end{array}\right]$ Similarly, for $\lambda=2$ $X_{2}=\left[\begin{array}{c}-2 \\ 1 \\ 2\end{array}\right]$ and for $\lambda=3$ $X_{3}=\left[\begin{array}{c}1 \\ -1 \\ -2\end{array}\right]$$

$Similarly, \\ for\ \lambda = 2 \\ X_2 = \begin{bmatrix} -2\\1\\2 \end{bmatrix} \\ and \\ for\ \lambda = 3 \\ X_3 = \begin{bmatrix} 1\\-1\\-2 \end{bmatrix}$

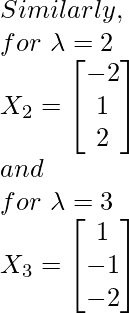
Paso 5: Creación de la array modal P. (aquí, X ₁ , X ₂ , X ₃ son vectores columna)

$P=\left[X_{1} X_{2} X_{3}\right]=\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right]$

Paso 6: Encontrar P ^-1 y luego poner valores en diagonalización de una ecuación matricial. [D = P ^-1AP]

Realizamos el Paso 6 para averiguar qué valor propio reemplazará a λ ₁ , λ ₂ y λ ₃ en la array diagonal inicial creada en el Paso 1.

$\begin{array}{l} \begin{array}{l} \quad P=\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right] \\ \operatorname{det}(P)=(1)[(-2)(1)-(-1)(2)]-(-2)[(-2)(-1)-(0)(-1)]+(1)[(2)(-1)- \\ (0)(1)] \\ =[0+(4)+(-2)] \\ =2 \end{array}\\ \text { Since } \operatorname{det}(P) \neq 0 \Longrightarrow \text { Matrix } P \text { is invertible. } \end{array}$

Lo sabemos $P^{-1}=\frac{\operatorname{adj}(P)}{\operatorname{det}(P)}$

Al resolver obtenemos $P^{-1}=\frac{1}{2}\left[\begin{array}{ccc} 0 & -2 & 1 \\ -2 & -2 & 0 \\ -2 & -2 & -1 \end{array}\right]$

Introduciendo la ecuación de Diagonalización de Matrix, obtenemos

$\begin{array}{l} \quad D=P^{-1} A P \\ D=\frac{1}{2}\left[\begin{array}{ccc} 0 & -2 & 1 \\ -2 & -2 & 0 \\ -2 & -2 & -1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & -1 \\ 1 & 2 & 1 \\ 2 & 2 & 3 \end{array}\right]\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right] \\ D=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array}\right] \end{array}$

Matlab

% MATLAB Implementation for
% Diagonalization of a Square Matrix:
clear all
clc      
disp("MATLAB Implementation for Diagonalization
 of a Square Matrix | GeeksforGeeks")
A = input("Enter a matrix A : ");
[P , D] = eig(A);
D1 = inv(P)*(A)*(P);
disp("Diagonal form 'D' of Input Matrix 'A' is:")
disp(D1)

Producción:

Para la array: $A = \begin{bmatrix} 1 & 3\\ 3 & 9\\ \end{bmatrix}$

Para la array: 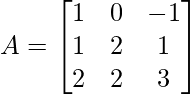$A = \begin{bmatrix} 1 & 0 & -1 \\ 1 & 2 & 1 \\ 2 & 2& 3\\ \end{bmatrix}$

Publicación traducida automáticamente

Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Problema de ejemplo:

Matlab

Deja una respuesta Cancelar la respuesta