Ecuación de un círculo

En matemáticas, un círculo es una forma que contiene todos los puntos en el plano y estos puntos son equidistantes del punto dado. Este punto dado se conoce como el centro del círculo. O dicho de otro modo, es una curva que es trazada por un punto que se mueve en un plano tal que su distancia a un punto fijo en ese plano es siempre constante. La distancia entre un punto del círculo y el centro del círculo se conoce como radio del círculo y cuando una cuerda pasa por el centro del círculo se conoce como diámetro o el círculo.

Ecuación estándar de un círculo

Para encontrar la forma estándar del círculo, supongamos que A(h, k) es el centro del círculo, r es el radio del círculo y P(x, y) es cualquier punto de la circunferencia. 

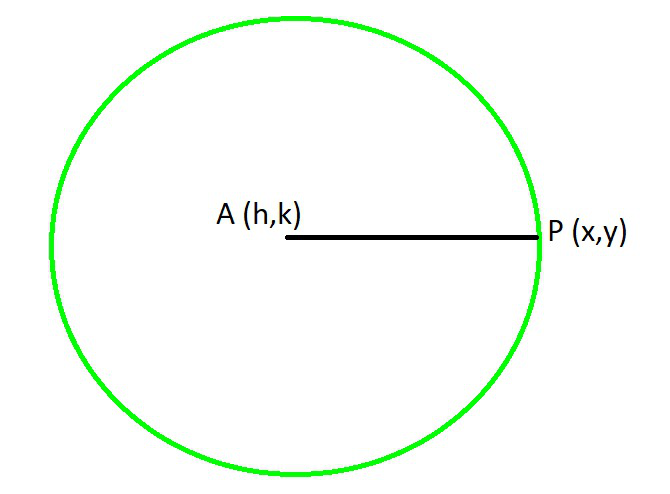
Entonces, AP = r …..(i)

Ahora usando la fórmula de la distancia encontramos el valor de AP

AP = 

Ahora ponga el valor de AP en la ecuación (i), obtenemos

 = r

O elevando al cuadrado ambos lados obtenemos

(x – h) ² + (y – k) ² = r ² 

Esta es la relación entre las coordenadas de cualquier punto de la circunferencia y, por lo tanto, es la ecuación requerida del círculo que tiene centro en A(h, k) y radio igual a r. Ahora veremos la variación en la ecuación estándar de un círculo:

Caso 1 : Cuando el centro del círculo está en el origen (0, 0) y el radio en r. 
h = 0 y k = 0 
Al sustituir en la ecuación estándar del círculo, obtenemos 
x ² + y ² = r ² 

Caso 2 : Cuando la circunferencia pasa por el origen. 
Aquí, sea el centro A(h, k) y O el origen que pasa por el círculo. 
Dibuja AM⊥OM 
In △AMO, OA ² = OM ² + AM ² 
r ² = h ² + k ² 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – h) ² + (y – k) ² = h ² + k ²  
x ² + y ² – 2hx – 2ky = 0 

Caso 3: Cuando el círculo tocó el eje x 
Aquí, sea el centro A(h, k). Como el círculo toca el eje x, 
k = r 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – h) ² + (y – r) ² = r ²  
x ² + y ² – 2hx – 2ry + h ² = 0 

Caso 4: Cuando el círculo tocó el eje x 
Aquí, sea el centro A(h, k). Como el círculo toca el eje x, 
h = r 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – r) ² + (y – k) ² = r ²  
x ² + y ² – 2rx – 2ky + k ² = 0 

Caso 5: Cuando el círculo tocó ambos ejes. 
Aquí, h = k = r 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – r) ² + (y – r) ² = r2 
x ² + y ² – 2rx – 2ry + r ² = 0 

Caso 6: Cuando la circunferencia pasa por el origen y el centro se encuentra en el eje x. 
Aquí, k = 0 y h = r 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – r) ² + (y – 0) ² = r ²  
x ² + y ² – 2rx = 0 

Caso 7: Cuando el círculo pasa por el origen y el centro se encuentra en el eje y. 
Aquí, h = 0 y k = r 
Al sustituir en la ecuación estándar del círculo, obtenemos 
(x – 0) ² + (y – r) ² = r ²  
x ² + y ² – 2ry = 0
 

Problemas de muestra

Pregunta 1. Encuentra el centro y el radio del círculo a partir de la ecuación dada:

x ² + (y + 2) ² = 9

Solución: 

Después de reorganizar, obtenemos

(x – 0) ² + (y – (-2)) ² = 3 ²

Al comparar con la ecuación estándar del círculo, tenemos

h = 0, k = -2 y r = 3

Entonces el centro del círculo es (0, -2)

y el radio del circulo = 3

Pregunta 2. Encuentra el centro y el radio del círculo a partir de la ecuación dada: 

x2 + ^{y2 +} 6x – 4y + 4 = 0

Solución:

Tenemos,

(x2 ⁺ 6x) + ( ^y2 – 4y) = – 4

Para que sea una identidad cuadrada perfecta, suma y resta 9 y 4,

(x2 ⁺ 6x + 9) + ( ^y2 – 4y + 4) – 9 – 4 = – 4

(x + 3) ² + (y – 2) ² = – 4 + 4 + 9

(x – (-3)) ² + (y – 2) ² = 9

(x – (-3)) ² + (y – 2) ² =3 ²

Al comparar con la ecuación estándar del círculo, tenemos

h = -3, k = 2 y r = 3

Entonces el centro del círculo es (-3, 2)

y el radio del circulo = 3

Graficar un círculo a partir de su ecuación estándar

Como sabemos que la ecuación estándar del círculo es 

(x – h) ² + (y – k) ² = r ² 

Aquí, el centro del círculo es (h, k) y el radio del círculo es r. Ahora tomemos un ejemplo:

La ecuación del círculo es (x + 2) ² + (y – 6) ² = 4

podemos reescribir esta ecuación como 

(x – (-2)) ² + (y – 6) ² = 2 ²

Al comparar con la ecuación estándar del círculo obtenemos

El centro del círculo es (-2, 6) y el radio del círculo es 2.

Ahora dibujaremos un círculo en el gráfico.

Paso 1: Dibuja los ejes x e y

Paso 2: Trace el centro del círculo en el gráfico que es (-2, 6)

Paso 3: Marque cuatro puntos en las cuatro direcciones desde el centro de los círculos y la distancia entre los puntos y el centro es 2.

Paso 4: Une todos estos puntos para obtener un círculo.
 

Ecuación expandida de un círculo

Ahora encontraremos la ecuación expandida de un círculo. Entonces, supongamos que A(h, k) sea el centro del círculo y r sea el radio del círculo y P(x, y) sea cualquier punto de la circunferencia. 

Entonces AP = r …(i)

En ángulo recto △ACP, 

AP ² = AC ² + PC ²

r ² = (x – h) ² + (y – k) ²

Ampliando aún más, obtenemos

(x – h) ² + (y – k) ² = r ²

(x ² – 2hx + h ² ) + (y ² – 2ky + k ² ) = r ²

y si llevamos r ² al lado izquierdo y lo reorganizamos obtenemos

La ecuación expandida del círculo:

x ² – 2hx + h ² + y ² – 2ky + k ² – r ² = 0 

Ejemplo: Encuentra el centro y el radio del círculo usando la siguiente ecuación: x ² + y ² – 4x + 6y = 12.

Solución:

Dado: x ² + y ² – 4x + 6y = 12

Podemos escribir como

(x ² – 4x) + (y ² – 6y) = 12

Al manipular la identidad, obtenemos

(x2 – 4x + 4) + ( ^{y2 –6y} + 9) – 9 – 4 = 12

(x ² – 4x + 4) + (y ² – 6y + 9) = 12 + 9 + 4

(x-2) ² + (y-3) ² = 25

(x – 2) ² + (y – 3) ² = 5 ²

Al comparar con la ecuación estándar del círculo, tenemos

h = 2, k = 3 y r = 5

Ecuación general de un círculo 

La ecuación general de un círculo es:

x ² + y ² + 2gx + 2fy + c = 0  

Para todos los valores de g, f y c.

Ahora, al sumar g ² + f ² en ambos lados de la ecuación, obtenemos

(x ² + 2gx + gramo ² )+ (y ² + 2fy + f ² ) = gramo ² + f ² − do 

Como, (x + g) ² = x ² + 2gx + g ² y (y + f) ² = y ² + 2fy + f ² 

(x + g) ² + (y + f) ² = gramo ² + f ² – c 

(x – (-g)) ² + (y – (-f)) ² = g ² + f ² – c ……….(1)

Al comparar la ecuación (1) con la ecuación estándar, obtenemos

h = −g, k = −f

r ² = gramo ² + F ² −c

donde (h, k) es el centro y ‘r’ es el radio del círculo.

Por eso,

x ² + y ² + 2gx + 2fy + c = 0, representa la circunferencia de centro (−g, −f) y radio (r) igual a r ² = g ² + f ² − c.

• Si g ² + f ² > c, entonces el radio del círculo es real .
• Si g ² + f ² = c, entonces el radio de la circunferencia es cero lo que nos dice que la circunferencia es un punto que coincide con el centro. Este tipo de círculo se llama círculo puntual.
• g ² + f ² <c, entonces el radio del círculo se vuelve imaginario . Por lo tanto, es un círculo que tiene un centro real y un radio imaginario. 

Algunas características de la ecuación general x ² + y ² + 2gx + 2fy + c = 0 del círculo son las siguientes:

• Es cuadrática tanto en x como en y.
• Coeficiente de x ² = y ² . (Es recomendable mantener el coeficiente de x ² e y ² unidad)
• No hay ningún término que contenga xy, es decir, el coeficiente de xy es cero.
• Contiene tres constantes arbitrarias a saber. g, f y c.

Problemas de muestra

Pregunta 1. Encuentra la ecuación de un círculo cuyo centro es (-3, -2) y radio 6.

Solución:

Dado: h = -3, k = -2 y r = 6

Usando la ecuación estándar del círculo, 

(x – h) ² + (y – k) ² = r ² 

(x – (-3)) ² + (y – (-2)) ² = 6 ²

(x + 3) ² + (y + 2) ² = 6 ²

x2 ⁺ 6x + 9 + ^y2 + 4y + 4 = 36

Por lo tanto, la ecuación requerida es

x2 + ^{y2 +} 6x + 4y – 23 = 0

Pregunta 2. Encuentra la ecuación de un círculo cuyo radio es 7 y el centro está en el origen.

Solución:

Dado: r = 7 y el centro = (0, 0)

Usando la ecuación estándar del círculo, 

(x – h) ² + (y – k) ² = r ² 

x ² + y ² = r ²

x ² + y ² = 7 ²

Por lo tanto, la ecuación requerida es

x2 + y2 ^– 49 = ⁰ 

Pregunta 3. Encuentra el radio y el centro del círculo dado por la ecuación

2x ² + 2y ² + 8x + 12y – 38 = 0

Solución:

En la ecuación dada, los coeficientes de x ² y y ² no son la unidad. 

En primer lugar, hagámoslos unidad dividiendo la ecuación por 2,

x2 + ^{y2 +} 4x + 6y – 19 = 0

Entonces, las coordenadas del centro son (-2, -3)

y, Radio = 

Radio = 

Radio = 4√2

Pregunta 4. Encuentra la ecuación del círculo que pasó por los puntos (1, 0), (-1, 0) y (0, 1).

Solución:

Deje que el círculo requerido sea 

x ² + y ² + 2gx + 2fy + c = 0

Como pasa por (1, 0), (-1, 0) y (0, 1). Por lo tanto, satisfarán la ecuación

Sustituyéndolos, obtenemos

1 + 2g + c = 0 ……..(1)

1 – 2g + c = 0 ……..(2)

1 + 2f + c = 0 ……..(3)

De la ecuación (1) y (2), obtenemos

g = 0 y c = -1

Ahora, poniendo c = -1 en la ecuación (3), obtenemos

f = 0

Ahora, sustituyendo los valores de g, f y c en la ecuación principal, obtenemos

x2 + ^y2 = ¹

Pregunta 5. Encuentra la ecuación de la imagen del círculo x ² + y ² + 16x – 8y + 64 = 0 en la línea espejo x = 0.

Solución:

La ecuación dada es:

x ² + y ² + 16x – 8y = – 64

(x2 ⁺ 16x) + ( ^y2 – 8y) = – 64

Al sumar y restar 64 y 16, obtenemos

(x2 ⁺ 16x + 64) + ( ^y2 – 8y + 16) – 64 – 16 = – 64

(x2 ⁺ 16x + 64) + ( ^y2 – 8y + 16) = – 64 + 64 + 16

(x + 8) ² + (y – 4) ² = 16

(x – (-8)) ² + (y – 4) ² = 4 ²

Como, el radio de este círculo es (-8, 4) y radio = 4.

La imagen del círculo en el espejo lineal tendrá su centro en (8, 4) y radio 4.

Entonces, la ecuación será,

(x – 8) ² + (y – 4) ² = 4 ²

x2 + ^{y2 – 16x – 8y +} 64 = 0