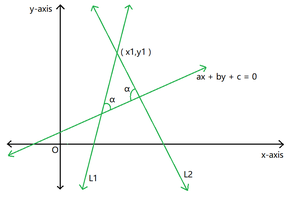
Dados cuatro números enteros a, b, c y d , que representan coeficientes de una recta con ecuación (ax + by + c = 0), la tarea es encontrar las ecuaciones de las dos rectas que pasan por un punto dado ![]() y forman un ángulo α con la recta dada.
y forman un ángulo α con la recta dada.
Ejemplos:
Entrada: a = 2, b = 3, c = -7, x1 = 4, y1 = 9, α = 30
Salida: y = -0,49x +10
y = -15,51x + 71Entrada: a = 3, b = -2, c = 4, x1 = 3, y1 = 4, α = 55
Salida: y = 43,73x -127
y = -0,39x +5
Acercarse:
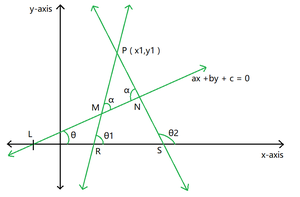
Figura 1
- Sea P (x1, y1) el punto dado y la línea LMN (en la figura 1) sea la línea dada que forma un ángulo θ con el eje x positivo.
- Sean PMR y PNS dos líneas requeridas que forman un ángulo (α) con la línea dada.
- Deje que estas líneas se encuentren con el eje x en R y S respectivamente.
- Suponga que la línea PMR y PNS forman ángulos (θ1) y (θ2) respectivamente con la dirección positiva del eje x.
- Luego, usando la forma de punto de pendiente de una línea recta , la ecuación de dos líneas es:
… (1)
… (2)
y
son las pendientes de las rectas PMR y PNS respectivamente.
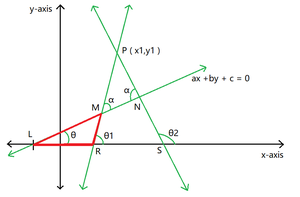
Figura 2
- Ahora considere el triángulo LMR :
Usando la propiedad: Un ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores opuestos

… (3)
- Ahora considere el triángulo LNS :
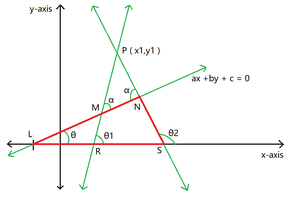
figura 3
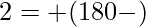
… (4)
- Ahora calculamos el valor de (tanθ):
Por fórmula,
pendiente de la línea dada
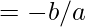
- Ahora sustituya los valores de (tan(θ1)) y (tan(θ2)) de las ecuaciones (3) y (4) a las ecuaciones (1) y (2) para obtener las ecuaciones finales de ambas líneas:
Línea PMR :
Línea PNS :
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find slope of given line
double line_slope(double a, double b)
{
if (a != 0)
return -b / a;
// Special case when slope of
// line is infinity or is
// perpendicular to x-axis
else
return (-2);
}
// Function to find equations of lines
// passing through the given point
// and making an angle with given line
void line_equation(double a, double b,
double c, double x1,
double y1, double alfa)
{
// Set the precision
cout << fixed << setprecision(2);
// Store slope of given line
double given_slope = line_slope(a, b);
// Convert degrees to radians
double x = alfa * 3.14159 / 180;
// Special case when slope of
// given line is infinity:
// In this case slope of one line
// will be equal to alfa
// and the other line will be
// equal to (180-alfa)
if (given_slope == -2) {
// In this case slope of
// required lines can't be
// infinity
double slope_1 = tan(x);
double slope_2 = tan(3.14159 - x);
// g and f are the variables
// of required equations
int g = x1, f = x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0)
cout << "y = " << slope_1
<< "x +" << g << endl;
if (g <= 0)
cout << "y = " << slope_1
<< "x " << g << endl;
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0) {
cout << "y = " << slope_2
<< "x +" << f << endl;
}
if (f <= 0)
cout << "y = " << slope_2
<< "x " << f << endl;
return;
}
// Special case when slope of
// required line becomes infinity
if (1 - tan(x) * given_slope == 0) {
cout << "x = " << x1 << endl;
}
if (1 + tan(x) * given_slope == 0) {
cout << "x = " << x1 << endl;
}
// General case
double slope_1 = (given_slope + tan(x))
/ (1 - tan(x) * given_slope);
double slope_2 = (given_slope - tan(x))
/ (1 + tan(x) * given_slope);
// g and f are the variables
// of required equations
int g = x1, f = x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0 && 1 - tan(x) * given_slope != 0)
cout << "y = " << slope_1
<< "x +" << g << endl;
if (g <= 0 && 1 - tan(x) * given_slope != 0)
cout << "y = " << slope_1
<< "x " << g << endl;
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0 && 1 + tan(x) * given_slope != 0) {
cout << "y = " << slope_2
<< "x +" << f << endl;
}
if (f <= 0 && 1 + tan(x) * given_slope != 0)
cout << "y = " << slope_2
<< "x " << f << endl;
}
// Driver Code
int main()
{
// Given Input
double a = 2, b = 3, c = -7;
double x1 = 4, y1 = 9;
double alfa = 30;
// Function Call
line_equation(a, b, c, x1, y1, alfa);
return 0;
}
Java
// Java program for the above approach
import java.io.*;
class GFG{
// Function to find slope of given line
static double line_slope(double a, double b)
{
if (a != 0)
return -b / a;
// Special case when slope of
// line is infinity or is
// perpendicular to x-axis
else
return (-2);
}
// Function to find equations of lines
// passing through the given point
// and making an angle with given line
static void line_equation(double a, double b,
double c, double x1,
double y1, double alfa)
{
// Store slope of given line
double given_slope = line_slope(a, b);
// Convert degrees to radians
double x = alfa * 3.14159 / 180;
// Special case when slope of
// given line is infinity:
// In this case slope of one line
// will be equal to alfa
// and the other line will be
// equal to (180-alfa)
if (given_slope == -2)
{
// In this case slope of
// required lines can't be
// infinity
double slope_1 = Math.tan(x);
double slope_2 = Math.tan(3.14159 - x);
// g and f are the variables
// of required equations
int g = (int)x1, f = (int)x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0)
System.out.println("y = " +
(Math.round(slope_1 * 100.0) / 100.0) +
"x +" + (Math.round(g * 100.0) / 100.0));
if (g <= 0)
System.out.println("y = " +
(Math.round(slope_1 * 100.0) / 100.0) +
"x " + (Math.round(g * 100.0) / 100.0));
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0)
{
System.out.println("y = " +
(Math.round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.round(f * 100.0) / 100.0));
}
if (f <= 0)
System.out.println("y = " +
(Math.round(slope_1 * 100.0) / 100.0) +
"x " + (Math.round(g * 100.0) / 100.0));
return;
}
// Special case when slope of
// required line becomes infinity
if (1 - Math.tan(x) * given_slope == 0)
{
System.out.println("x = " +
(Math.round(x1 * 100.0) / 100.0));
}
if (1 + Math.tan(x) * given_slope == 0)
{
System.out.println("x = " +
(Math.round(x1 * 100.0) / 100.0));
}
// General case
double slope_1 = (given_slope + Math.tan(x)) /
(1 - Math.tan(x) * given_slope);
double slope_2 = (given_slope - Math.tan(x)) /
(1 + Math.tan(x) * given_slope);
// g and f are the variables
// of required equations
int g = (int)x1, f = (int)x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0 && 1 - Math.tan(x) * given_slope != 0)
System.out.println("y = " +
(Math.round(slope_1 * 100.0) / 100.0) +
"x +" + (Math.round(g * 100.0) / 100.0));
if (g <= 0 && 1 - Math.tan(x) * given_slope != 0)
System.out.println("y = " +
(Math.round(slope_1 * 100.0) / 100.0) +
"x " + (Math.round(g * 100.0) / 100.0));
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0 && 1 + Math.tan(x) * given_slope != 0)
{
System.out.println("y = " +
(Math.round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.round(f * 100.0) / 100.0));
}
if (f <= 0 && 1 + Math.tan(x) * given_slope != 0)
System.out.println("y = " +
(Math.round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.round(f * 100.0) / 100.0));
}
// Driver Code
public static void main (String[] args)
{
// Given Input
double a = 2, b = 3, c = -7;
double x1 = 4, y1 = 9;
double alfa = 30;
// Function Call
line_equation(a, b, c, x1, y1, alfa);
}
}
// This code is contributed by Dharanendra L V.
Python3
# Python3 program for the above approach
import math
# Function to find slope of given line
def line_slope(a, b):
if (a != 0):
return -b / a
# Special case when slope of
# line is infinity or is
# perpendicular to x-axis
else:
return (-2)
# Function to find equations of lines
# passing through the given point
# and making an angle with given line
def line_equation(a, b, c, x1, y1, alfa):
# Store slope of given line
given_slope = line_slope(a, b)
# Convert degrees to radians
x = alfa * 3.14159 / 180
# Special case when slope of
# given line is infinity:
# In this case slope of one line
# will be equal to alfa
# and the other line will be
# equal to (180-alfa)
if (given_slope == -2):
# In this case slope of
# required lines can't be
# infinity
slope_1 = math.tan(x)
slope_2 = math.tan(3.14159 - x)
# g and f are the variables
# of required equations
g = x1, f = x1
g *= (-slope_1)
g += y1
# Print first line equation
if (g > 0):
print("y = ", round(slope_1, 2),
"x +" , round(g));
if (g <= 0):
print("y = ", round(slope_1, 2),
"x ", round(g))
f *= (-slope_2)
f += y1
# Print second line equation
if (f > 0):
print("y = ", round(slope_2, 2),
"x +", round(f))
if (f <= 0):
print("y = " , round(slope_2, 2),
"x " , round(f))
return
# Special case when slope of
# required line becomes infinity
if (1 - math.tan(x) * given_slope == 0):
print("x =", x1)
if (1 + math.tan(x) * given_slope == 0):
print("x =", x1)
# General case
slope_1 = ((given_slope + math.tan(x)) /
(1 - math.tan(x) * given_slope))
slope_2 = ((given_slope - math.tan(x)) /
(1 + math.tan(x) * given_slope))
# g and f are the variables
# of required equations
g = x1
f = x1
g *= (-slope_1)
g += y1
# Print first line equation
if (g > 0 and 1 - math.tan(x) * given_slope != 0):
print("y = ", round(slope_1, 2),
"x +", round(g))
if (g <= 0 and 1 - math.tan(x) * given_slope != 0):
print("y = ", round(slope_1, 2),
"x ", round(g))
f *= (-slope_2)
f += y1
# Print second line equation
if (f > 0 and 1 + math.tan(x) * given_slope != 0):
print("y = ", round(slope_2, 2),
"x +", round(f))
if (f <= 0 and 1 + math.tan(x) * given_slope != 0):
print("y = ", round(slope_2, 2),
"x " , round(f))
# Driver Code
if __name__ == "__main__":
# Given Input
a = 2
b = 3
c = -7
x1 = 4
y1 = 9
alfa = 30
# Function Call
line_equation(a, b, c, x1, y1, alfa)
# This code is contributed by ukasp
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
public class GFG{
// Function to find slope of given line
static double line_slope(double a, double b)
{
if (a != 0)
return -b / a;
// Special case when slope of
// line is infinity or is
// perpendicular to x-axis
else
return (-2);
}
// Function to find equations of lines
// passing through the given point
// and making an angle with given line
static void line_equation(double a, double b,
double c, double x1,
double y1, double alfa)
{
// Store slope of given line
double given_slope = line_slope(a, b);
// Convert degrees to radians
double x = alfa * 3.14159 / 180;
double slope_1,slope_2;
double g,f;
// Special case when slope of
// given line is infinity:
// In this case slope of one line
// will be equal to alfa
// and the other line will be
// equal to (180-alfa)
if (given_slope == -2)
{
// In this case slope of
// required lines can't be
// infinity
slope_1 = Math.Tan(x);
slope_2 = Math.Tan(3.14159 - x);
// g and f are the variables
// of required equations
g = (int)x1;
f = (int)x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0)
Console.WriteLine("y = " +
(Math.Round(slope_1 * 100.0) / 100.0) +
"x +" + (Math.Round((int)g * 100.0) / 100.0));
if (g <= 0)
Console.WriteLine("y = " +
(Math.Round(slope_1 * 100.0) / 100.0) +
"x " + (Math.Round((int)g * 100.0) / 100.0));
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0)
{
Console.WriteLine("y = " +
(Math.Round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.Round((int)f * 100.0) / 100.0));
}
if (f <= 0)
Console.WriteLine("y = " +
(Math.Round(slope_1 * 100.0) / 100.0) +
"x " + (Math.Round((int)g * 100.0) / 100.0));
return;
}
// Special case when slope of
// required line becomes infinity
if (1 - Math.Tan(x) * given_slope == 0)
{
Console.WriteLine("x = " +
(Math.Round(x1 * 100.0) / 100.0));
}
if (1 + Math.Tan(x) * given_slope == 0)
{
Console.WriteLine("x = " +
(Math.Round(x1 * 100.0) / 100.0));
}
// General case
slope_1 = (given_slope + Math.Tan(x)) /
(1 - Math.Tan(x) * given_slope);
slope_2 = (given_slope - Math.Tan(x)) /
(1 + Math.Tan(x) * given_slope);
// g and f are the variables
// of required equations
g = (int)x1;
f = (int)x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0 && 1 - Math.Tan(x) * given_slope != 0)
Console.WriteLine("y = " +
(Math.Round(slope_1 * 100.0) / 100.0) +
"x +" + (Math.Round((int)g * 100.0) / 100.0));
if (g <= 0 && 1 - Math.Tan(x) * given_slope != 0)
Console.WriteLine("y = " +
(Math.Round(slope_1 * 100.0) / 100.0) +
"x " + (Math.Round((int)g * 100.0) / 100.0));
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0 && 1 + Math.Tan(x) * given_slope != 0)
{
Console.WriteLine("y = " +
(Math.Round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.Round((int)f * 100.0) / 100.0));
}
if (f <= 0 && 1 + Math.Tan(x) * given_slope != 0)
Console.WriteLine("y = " +
(Math.Round(slope_2 * 100.0) / 100.0) +
"x +" + (Math.Round((int)f * 100.0) / 100.0));
}
// Driver Code
public static void Main(String[] args)
{
// Given Input
double a = 2, b = 3, c = -7;
double x1 = 4, y1 = 9;
double alfa = 30;
// Function Call
line_equation(a, b, c, x1, y1, alfa);
}
}
// This code contributed by shikhasingrajput
Javascript
// JavaScript program for the above approach
// Function to find slope of given line
function line_slope(a, b)
{
if (a != 0)
return -b / a;
// Special case when slope of
// line is infinity or is
// perpendicular to x-axis
else
return (-2);
}
// Function to find equations of lines
// passing through the given point
// and making an angle with given line
function line_equation(a, b, c, x1, y1, alfa)
{
// Store slope of given line
let given_slope = line_slope(a, b);
// Convert degrees to radians
let x = alfa * 3.14159 / 180;
// Special case when slope of
// given line is infinity:
// In this case slope of one line
// will be equal to alfa
// and the other line will be
// equal to (180-alfa)
if (given_slope == -2) {
// In this case slope of
// required lines can't be
// infinity
let slope_1 = Math.tan(x);
let slope_2 = Math.tan(3.14159 - x);
// g and f are the variables
// of required equations
let g = x1, f = x1;
g = g*(-slope_1);
g = g + y1;
// Print first line equation
if (g > 0)
console.log("y = ", slope_1.toFixed(2), "x +", Math.floor(g));
if (g <= 0)
console.log("y = ", slope_1.toFixed(2), "x ", Math.floor(g));
f = f*(-slope_2);
f = f+y1;
// Print second line equation
if (f > 0) {
console.log("y = ", slope_2.toFixed(2), "x +", Math.floor(f));
}
if (f <= 0){
console.log("y = ", slope_2.toFixed(2), "x ", Math.floor(f));
}
return;
}
// Special case when slope of
// required line becomes infinity
if (1 - Math.tan(x) * given_slope == 0) {
console.log("x = ", x1.toFixed(2));
}
if (1 + Math.tan(x) * given_slope == 0) {
console.log("x = ", x1.toFixed(2));
}
// General case
let slope_1 = (given_slope + Math.tan(x))
/ (1 - Math.tan(x) * given_slope);
let slope_2 = (given_slope - Math.tan(x))
/ (1 + Math.tan(x) * given_slope);
// g and f are the variables
// of required equations
let g = x1, f = x1;
g *= (-slope_1);
g += y1;
// Print first line equation
if (g > 0 && 1 - Math.tan(x) * given_slope != 0)
console.log("y = ", slope_1.toFixed(2), "x +", Math.floor(g));
if (g <= 0 && 1 - tan(x) * given_slope != 0)
console.log("y = ", slope_1.toFixed(2), "x ", Math.floor(g));
f *= (-slope_2);
f += y1;
// Print second line equation
if (f > 0 && 1 + Math.tan(x) * given_slope != 0) {
console.log("y = ", slope_2.toFixed(2), "x +", Math.floor(f));
}
if (f <= 0 && 1 + tan(x) * given_slope != 0)
console.log("y = ", slope_2.toFixed(2), "x ", Math.floor(f));
}
// Driver Code
// Given Input
let a = 2, b = 3, c = -7;
let x1 = 4, y1 = 9;
let alfa = 30;
// Function Call
line_equation(a, b, c, x1, y1, alfa);
// The code is contributed by Gautam goel (gautamgoel962)
y = -0.49x +10 y = -15.51x +71
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por arjundevmishra6 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA