El mayor valor de x tal que axx es un número de N dígitos de base b

Dados los números enteros a , b , N , la tarea es encontrar el mayor número x tal que $a*x^{x}$ sea un número de N dígitos de base b.

Ejemplos:

Entrada: a = 2, b = 10, N = 2
Salida: 3
Explicación:
Aquí 2 * 3 ³ = 54, que tiene el número de dígitos = 2,
pero 2 * 4 ⁴ = 512 que tiene el número de dígitos = 3 , que no es igual a N.
Por lo tanto, el mayor valor de x es 2.

Entrada: a = 1, b = 2, N = 3
Salida: 2
Explicación:
1 * 2 ² = 4 cuya representación binaria es 100 y tiene 3 dígitos.

Enfoque: este problema se puede resolver mediante la búsqueda binaria .

El número de dígitos de 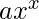$ax^x$ en base 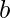$b$ es $\lceil\log_b{ax^x}\rceil$ .
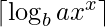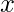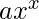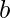La búsqueda binaria se utiliza para encontrar el mayor $x$ de modo que el número de dígitos de la $ax^x$ base $b$ sea exactamente $n$ .
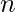En la búsqueda binaria, comprobaremos el número de dígitos 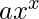$ax^x$ , donde 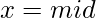$x = mid$ , y cambiaremos el puntero de acuerdo con eso.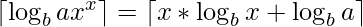
$\lceil\log_b{ax^x}\rceil = \lceil x*\log_b{x}+\log_b{a} \rceil$

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation of the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find log_b(a)
double log(int a, int b)
{
    return log10(a) / log10(b);
}
 
int get(int a, int b, int n)
{
 
    // Set two pointer for binary search
    int lo = 0, hi = 1e6;
 
    int ans = 0;
 
    while (lo <= hi) {
        int mid = (lo + hi) / 2;
 
        // Calculating number of digits
        // of a*mid^mid in base b
        int dig = ceil((mid * log(mid, b)
                        + log(a, b)));
 
        if (dig > n) {
 
            // If number of digits > n
            // we can simply ignore it
            // and decrease our pointer
            hi = mid - 1;
        }
        else {
 
            // if number of digits <= n,
            // we can go higher to
            // reach value exactly equal to n
            ans = mid;
            lo = mid + 1;
        }
    }
 
    // return the largest value of x
    return ans;
}
 
// Driver Code
int main()
{
 
    int a = 2, b = 2, n = 6;
 
    cout << get(a, b, n)
         << "\n";
 
    return 0;
}

Java

// Java implementation of the above approach
import java.util.*;
 
class GFG{
 
// Function to find log_b(a)
static int log(int a, int b)
{
    return (int)(Math.log10(a) /
                 Math.log10(b));
}
 
static int get(int a, int b, int n)
{
 
    // Set two pointer for binary search
    int lo = 0, hi = (int) 1e6;
 
    int ans = 0;
 
    while (lo <= hi)
    {
        int mid = (lo + hi) / 2;
 
        // Calculating number of digits
        // of a*mid^mid in base b
        int dig = (int) Math.ceil((mid * log(mid, b) +
                                         log(a, b)));
 
        if (dig > n)
        {
 
            // If number of digits > n
            // we can simply ignore it
            // and decrease our pointer
            hi = mid - 1;
        }
        else
        {
 
            // If number of digits <= n,
            // we can go higher to reach
            // value exactly equal to n
            ans = mid;
            lo = mid + 1;
        }
    }
 
    // Return the largest value of x
    return ans;
}
 
// Driver Code
public static void main(String[] args)
{
    int a = 2, b = 2, n = 6;
 
    System.out.print(get(a, b, n) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

Python3

# Python3 implementation of the above approach
 
from math import log10,ceil,log
 
# Function to find log_b(a)
def log1(a,b):
    return log10(a)//log10(b)
 
def get(a,b,n):
    # Set two pointer for binary search
    lo = 0
    hi = 1e6
 
    ans = 0
 
    while (lo <= hi):
        mid = (lo + hi) // 2
 
        # Calculating number of digits
        # of a*mid^mid in base b
        dig = ceil((mid * log(mid, b) + log(a, b)))
 
        if (dig > n):
            # If number of digits > n
            # we can simply ignore it
            # and decrease our pointer
            hi = mid - 1
 
        else:
            # if number of digits <= n,
            # we can go higher to
            # reach value exactly equal to n
            ans = mid
            lo = mid + 1
 
    # return the largest value of x
    return ans
 
# Driver Code
if __name__ == '__main__':
    a = 2
    b = 2
    n = 6
 
    print(int(get(a, b, n)))
 
# This code is contributed by Surendra_Gangwar

C#

// C# implementation of the above approach
using System;
class GFG{
 
// Function to find log_b(a)
static int log(int a, int b)
{
    return (int)(Math.Log10(a) /
                 Math.Log10(b));
}
 
static int get(int a, int b, int n)
{
 
    // Set two pointer for binary search
    int lo = 0, hi = (int) 1e6;
 
    int ans = 0;
 
    while (lo <= hi)
    {
        int mid = (lo + hi) / 2;
 
        // Calculating number of digits
        // of a*mid^mid in base b
        int dig = (int)Math.Ceiling((double)(mid *
                                         log(mid, b) +
                                         log(a, b)));
 
        if (dig > n)
        {
 
            // If number of digits > n
            // we can simply ignore it
            // and decrease our pointer
            hi = mid - 1;
        }
        else
        {
 
            // If number of digits <= n,
            // we can go higher to reach
            // value exactly equal to n
            ans = mid;
            lo = mid + 1;
        }
    }
 
    // Return the largest value of x
    return ans;
}
 
// Driver Code
public static void Main(String[] args)
{
    int a = 2, b = 2, n = 6;
 
    Console.Write(get(a, b, n) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

Javascript

<script>
 
// Javascript implementation of the above approach
 
// Function to find log_b(a)
function log(a, b)
{
    return (Math.log10(a) /
                 Math.log10(b));
}
   
function get(a, b, n)
{
   
    // Set two pointer for binary search
    let lo = 0, hi = 1e6;
   
    let ans = 0;
   
    while (lo <= hi)
    {
        let mid = Math.floor((lo + hi) / 2);
   
        // Calculating number of digits
        // of a*mid^mid in base b
        let dig =  Math.ceil((mid * log(mid, b) +
                                         log(a, b)));
   
        if (dig > n)
        {
   
            // If number of digits > n
            // we can simply ignore it
            // and decrease our pointer
            hi = mid - 1;
        }
        else
        {
   
            // If number of digits <= n,
            // we can go higher to reach
            // value exactly equal to n
            ans = mid;
            lo = mid + 1;
        }
    }
   
    // Return the largest value of x
    return ans;
}
// Driver Code
     
    let a = 2, b = 2, n = 6;
   
    document.write(get(a, b, n) + "\n");
                       
</script>

Producción:

Publicación traducida automáticamente

Artículo escrito por souradeep y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta