Encuentra el ángulo entre las tangentes dibujadas desde un punto externo dado a un círculo

Dado un número entero positivo R que representa el radio del círculo y el centro del círculo (X1, Y1) y otro punto (X2, Y2) en el plano cartesiano, la tarea es encontrar el ángulo entre el par de tangentes dibujadas desde el punto (X2, Y2) al círculo.

Ejemplos:

Entrada: R = 6, (X1, Y1) = (5, 1), (X2, Y2) = (6, 9)
Salida: 96.1851

Entrada: R = 4, (X1, Y1) = (7, 12), (X2, Y2) = (3, 4)
Salida: 53.1317

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones:

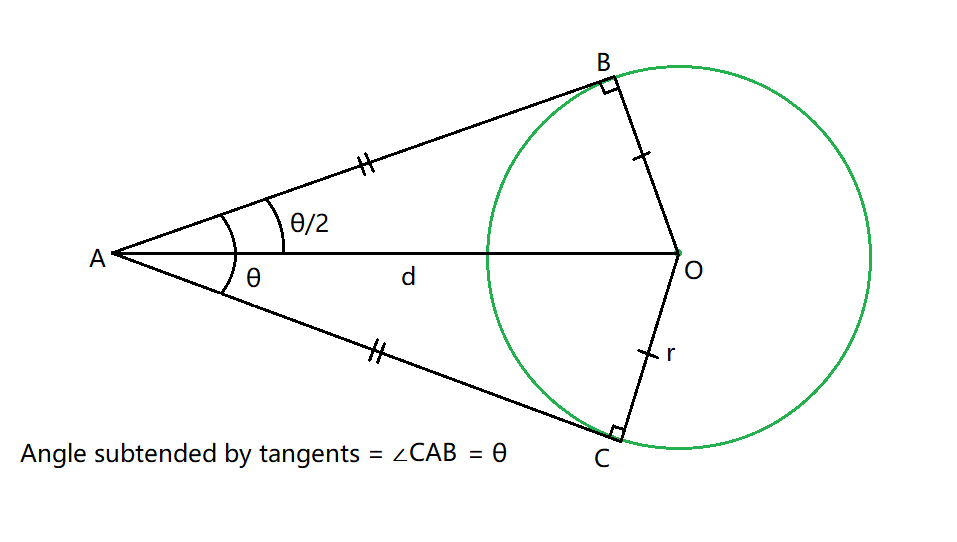
El radio forma un ángulo de 90 grados con la tangente en el punto de contacto de la tangente y el círculo. Además, el ángulo subtendido por el par de tangentes (θ) es bisecado por la línea que une el centro del círculo y el punto exterior.
Por lo tanto, la distancia entre el centro y el punto exterior se puede calcular usando la fórmula de la distancia como:

Distancia = $\sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)$

Ahora, considere d como la distancia entre los dos puntos dados, entonces En el triángulo rectángulo OAB,

=> $sin (\frac{\theta}{2}) = \frac{OB}{OA}$

=> $sin (\frac{\theta}{2}) = \frac{r}{d}$

=> $\frac{\theta}{2} = sin^{-1}(\frac{r}{d})$

=> $\theta = 2*sin^{-1}(\frac{r}{d})$

Por lo tanto, utilizando la fórmula anterior, se puede calcular el ángulo entre el par de tangentes trazadas desde el punto (X2, Y2) al círculo.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
 
#include <cmath>
#include <iostream>
using namespace std;
 
// Function to find the distance between
// center and the exterior point
double point_distance(int x1, int y1,
                      int x2, int y2)
{
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
 
    // Using the distance formula
    double distance = sqrt(p * p
                           + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
void tangentAngle(int x1, int y1,
                  int x2, int y2,
                  double radius)
{
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(
        x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1
        || radius / distance < -1) {
        cout << -1;
    }
 
    // Find the angle using the formula
    double result
        = 2 * asin(radius / distance) * 180
          / 3.1415;
 
    // Print the resultant angle
    cout << result << " degrees";
}
 
// Driver Code
int main()
{
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
    tangentAngle(x1, y1, x2, y2, radius);
 
    return 0;
}

Java

// java program for the above approach
import java.io.*;
import java.lang.*;
import java.util.*;
 
class GFG
{
   
// Function to find the distance between
// center and the exterior point
static double point_distance(int x1, int y1,
                      int x2, int y2)
{
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
  
    // Using the distance formula
    double distance = Math.sqrt(p * p
                           + q * q);
  
    return distance;
}
  
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
static void tangentAngle(int x1, int y1,
                  int x2, int y2,
                  double radius)
{
   
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(
        x1, y1, x2, y2);
  
    // Invalid Case
    if (radius / distance > 1
        || radius / distance < -1) {
         System.out.println(-1);
    }
  
    // Find the angle using the formula
    double result
        = 2 * Math.asin(radius / distance) * 180
          / 3.1415;
  
    // Print the resultant angle
    System.out.println(String.format("%.4f", result) + " degrees");
}
   
    // Driver Code
    public static void main(String[] args)
    {
 
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
    tangentAngle(x1, y1, x2, y2, radius);
    }
}
 
// This code is contributed by susmitakundugoaldanga.

Python3

# Python 3 program for the above approach
import math
 
# Function to find the distance between
# center and the exterior point
def point_distance(x1, y1,
                   x2,  y2):
 
    # Find the difference between
    # the x and y coordinates
    p = (x2 - x1)
    q = (y2 - y1)
 
    # Using the distance formula
    distance = math.sqrt(p * p
                         + q * q)
 
    return distance
 
# Function to find the angle between
# the pair of tangents drawn from the
# point (X2, Y2) to the circle.
def tangentAngle(x1,  y1,
                 x2,  y2,
                 radius):
 
    # Calculate the distance between
    # the center and exterior point
    distance = point_distance(
        x1, y1, x2, y2)
 
    # Invalid Case
    if (radius / distance > 1
            or radius / distance < -1):
        print(-1)
 
    # Find the angle using the formula
    result = 2 * math.asin(radius / distance) * 180 / 3.1415
 
    # Print the resultant angle
    print(result, " degrees")
 
# Driver Code
if __name__ == "__main__":
 
    radius = 4
    x1 = 7
    y1 = 12
    x2 = 3
    y2 = 4
    tangentAngle(x1, y1, x2, y2, radius)
 
    # This code is contributed by ukasp.

C#

// C# program for the above approach
using System;
 
class GFG{
 
// Function to find the distance between
// center and the exterior point
static double point_distance(int x1, int y1,
                             int x2, int y2)
{
     
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
 
    // Using the distance formula
    double distance = Math.Sqrt(p * p + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
static void tangentAngle(int x1, int y1, int x2,
                         int y2, double radius)
{
 
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1 ||
        radius / distance < -1)
    {
        Console.WriteLine(-1);
    }
 
    // Find the angle using the formula
    double result = 2 * Math.Asin(
               radius / distance) *
                  180 / 3.1415;
 
    // Print the resultant angle
    Console.WriteLine(
        String.Format("{0:0.0000}", result) +
                      " degrees");
}
 
// Driver code
static void Main()
{
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
     
    tangentAngle(x1, y1, x2, y2, radius);
}
}
 
// This code is contributed by abhinavjain194

Javascript

<script>
 
// JavaScript program for the above approach
 
 
// Function to find the distance between
// center and the exterior point
function  point_distance( x1,  y1, x2,  y2)
{
     
    // Find the difference between
    // the x and y coordinates
    var p = (x2 - x1);
    var q = (y2 - y1);
 
    // Using the distance formula
    var distance = Math.sqrt(p * p + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
 
function tangentAngle( x1,  y1,  x2, y2,  radius)
{
 
    // Calculate the distance between
    // the center and exterior point
    var distance = point_distance(x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1 ||
        radius / distance < -1)
    {
        document.write(-1 + "<br>");
    }
 
    // Find the angle using the formula
    var result = 2 * Math.asin(
               radius / distance) *
                  180 / 3.1415;
 
    // Print the resultant angle
    document.write( result.toFixed(4) + " degrees");
     
}
 
// Driver code
 
    var radius = 4;
    var x1 = 7, y1 = 12;
    var x2 = 3, y2 = 4;
     
    tangentAngle(x1, y1, x2, y2, radius);
     
</script>

Producción:

53.1317 degrees

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por arjundevmishra6 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta