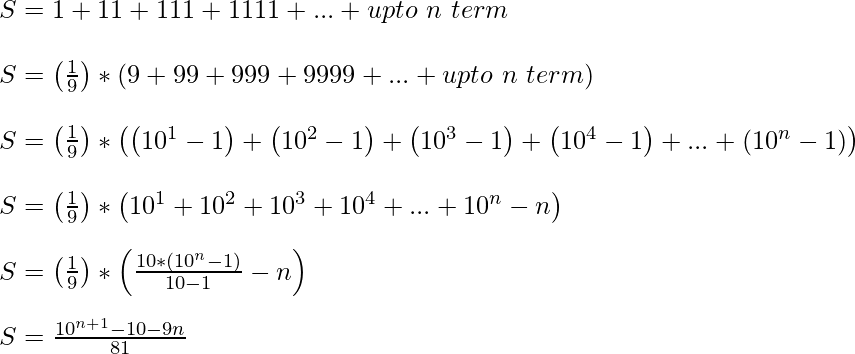Aquí vamos a encontrar la suma de la serie 1 + 11 + 111 + 1111 +…..hasta N términos (donde se da N).
Ejemplo :
Input : 3
Output : 1 + 11 + 111 +....
Total sum is : 123
Input : 4
Output : 1 + 11 + 111 + 1111 +.....
Total sum is : 1234
Input : 7
Output : 1 + 11 + 111 + 1111 + 11111 +
111111 + 1111111 +.....
Total sum is : 1234567
Aquí vemos que cuando el valor de N es 3, la serie dura hasta 1 + 11 + 111, es decir, tres términos y su suma es 123.
Programa para encontrar la suma de la serie anterior:
C++
// C++ program to find the sum of
// the series 1+11+111+1111+....
#include <bits/stdc++.h>
using namespace std;
// Function for finding summation
int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++) {
sum = sum + j;
// Appending a 1 at the end
j = (j * 10) + 1;
}
return sum;
}
// Driver Code
int main()
{
int n = 5;
cout << " " << summation(n);
return 0;
}
// This code is contributed by shivanisinghss2110
C
// C program to find the sum of
// the series 1+11+111+1111+....
#include <stdio.h>
// Function for finding summation
int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++) {
sum = sum + j;
// Appending a 1 at the end
j = (j * 10) + 1;
}
return sum;
}
// Driver Code
int main()
{
int n = 5;
printf("%d", summation(n));
return 0;
}
Java
// Java program to find the sum of
// the series 1+11+111+1111+....
import java.io.*;
class GFG
{
// Function for finding summation
static int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++)
{
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
// Driver Code
public static void main(String args[])
{
int n = 5;
System.out.println(summation(n));
}
}
// This code is contributed
// by Nikita Tiwari
Python
# Python program to get the summation # of following series def summation(n): sum = 0 j = 1 for i in range(1, n + 1): sum = sum + j j = (j * 10) + 1 return sum # Driver Code n = 5 print(summation(n))
C#
// C# program to find the sum of
// the series 1+11+111+1111+....
using System;
class GFG
{
// Function for finding summation
static int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++)
{
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
// Driver Code
public static void Main()
{
int n = 5;
Console.WriteLine(summation(n));
}
}
// This code is contributed by vt_m
PHP
<?php
// PHP program to find the sum of
// the series 1+11+111+1111+....
// Function for finding summation
function summation($n)
{
$sum = 0; $j = 1;
for ($i = 1; $i <= $n; $i++)
{
$sum = $sum + $j;
// Appending a 1 at the end
$j = ($j * 10) + 1;
}
return $sum;
}
// Driver Code
$n = 5;
echo summation($n);
// This code is contributed by ajit
?>
Javascript
<script>
// Javascript program to find the sum of
// the series 1+11+111+1111+....
// Function for finding summation
function summation( n) {
let sum = 0, j = 1;
for ( let i = 1; i <= n; i++) {
sum = sum + j;
// Appending a 1 at the end
j = (j * 10) + 1;
}
return sum;
}
// Driver Code
let n = 5;
document.write(summation(n));
// This code contributed by Princi Singh
</script>
Producción :
12345
Complejidad de tiempo: O(n), donde n representa el entero dado.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Otro método: Sea dada una serie S = 1 + 11 + 111 + 1111 + . . . + hasta el término n. Usando la fórmula para encontrar la suma de la serie.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to find the sum of
// the series 1+11+111+1111+....
#include <bits/stdc++.h>
// Function for finding summation
int summation(int n)
{
int sum;
sum = (pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
// Driver Code
int main()
{
int n = 5;
printf("%d", summation(n));
return 0;
}
Java
// java program to find the sum of
// the series 1+11+111+1111+....
import java.io.*;
class GFG {
// Function for finding summation
static int summation(int n)
{
int sum;
sum = (int)(Math.pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
// Driver Code
public static void main (String[] args)
{
int n = 5;
System.out.println(summation(n));
}
}
// This code is contributed by anuj_67.
Python3
# Python3 program to # find the sum of # the series 1+11+111+1111+.... import math # Function for # finding summation def summation(n): return int((pow(10, n + 1) - 10 - (9 * n)) / 81); # Driver Code print(summation(5)); # This code is contributed # by mits.
C#
// C# program to find the sum of
// the series 1+11+111+1111+....
using System;
class GFG {
// Function for finding summation
static int summation(int n)
{
int sum;
sum = (int)(Math.Pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
// Driver Code
public static void Main ()
{
int n = 5;
Console.WriteLine(summation(n));
}
}
// This code is contributed by anuj_67.
PHP
<?php
//PHP program to find the sum of
// the series 1+11+111+1111+....
// Function for finding summation
function summation($n)
{
$sum;
$sum = (pow(10, $n + 1) -
10 - (9 * $n)) / 81;
return $sum;
}
// Driver Code
$n = 5;
echo summation($n);
// This code is contributed by aj_36
?>
Javascript
<script>
// javascript program to find the sum of
// the series 1+11+111+1111+....
// Function for finding summation
function summation( n)
{
let sum;
sum = (Math.pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
// Driver Code
let n = 5;
document.write(summation(n)) ;
// This code is contributed by aashish1995
</script>
Producción :
12345
Complejidad de tiempo: O(logn), donde n representa el entero dado.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Publicación traducida automáticamente
Artículo escrito por Kanchan_Ray y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA