Dado un número N , la tarea es encontrar el N-ésimo término en la serie 12, 35, 81, 173, 357, …
Ejemplo:
Input: N = 2
Output: 35
2nd term = (12*2) + 11
= 35
Input: N = 5
Output: 357
5th term = (12*(2^4))+11*((2^4)-1)
= 357
Acercarse:
- Todos y cada uno de los números se obtienen multiplicando el número anterior por 2 y sumándole 11.
- Dado que el número inicial es 12.
1st term = 12 2nd term = (12 * 2) / 11 = 35 3rd term = (35 * 2) / 11 = 81 4th term = (81 * 2) / 11 = 173 And, so on....
- En general, el número N se obtiene mediante la fórmula:
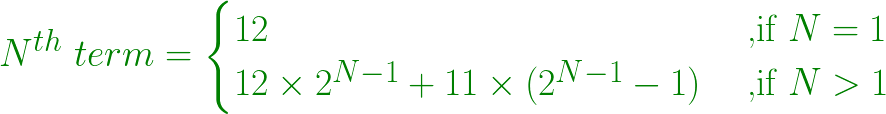
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find the Nth term
// in series 12, 35, 81, 173, 357, ...
#include <bits/stdc++.h>
using namespace std;
// Function to find Nth term
int nthTerm(int N)
{
int nth = 0, first_term = 12;
// Nth term
nth = (first_term * (pow(2, N - 1)))
+ 11 * ((pow(2, N - 1)) - 1);
return nth;
}
// Driver Method
int main()
{
int N = 5;
cout << nthTerm(N) << endl;
return 0;
}
Java
// Java program to find the Nth term
// in series 12, 35, 81, 173, 357, ...
class GFG
{
// Function to find Nth term
static int nthTerm(int N)
{
int nth = 0, first_term = 12;
// Nth term
nth = (int) ((first_term * (Math.pow(2, N - 1)))
+ 11 * ((Math.pow(2, N - 1)) - 1));
return nth;
}
// Driver code
public static void main(String[] args)
{
int N = 5;
System.out.print(nthTerm(N) +"\n");
}
}
// This code is contributed by Rajput-Ji
Python3
# Python3 program to find the Nth term # in series 12, 35, 81, 173, 357, ... # Function to find Nth term def nthTerm(N) : nth = 0; first_term = 12; # Nth term nth = (first_term * (pow(2, N - 1))) + \ 11 * ((pow(2, N - 1)) - 1); return nth; # Driver Method if __name__ == "__main__" : N = 5; print(nthTerm(N)) ; # This code is contributed by AnkitRai01
C#
// C# program to find the Nth term
// in series 12, 35, 81, 173, 357, ...
using System;
class GFG
{
// Function to find Nth term
static int nthTerm(int N)
{
int nth = 0, first_term = 12;
// Nth term
nth = (int) ((first_term * (Math.Pow(2, N - 1)))
+ 11 * ((Math.Pow(2, N - 1)) - 1));
return nth;
}
// Driver code
public static void Main(String[] args)
{
int N = 5;
Console.Write(nthTerm(N) +"\n");
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript program to find the Nth term
// in series 12, 35, 81, 173, 357, ...
// Function to find Nth term
function nthTerm(N)
{
let nth = 0, first_term = 12;
// Nth term
nth = (first_term * (Math.pow(2, N - 1)))
+ 11 * ((Math.pow(2, N - 1)) - 1);
return nth;
}
let N = 5;
document.write(nthTerm(N));
// This code is contributed by divyeshrabadiya07.
</script>
Producción:
357
Complejidad del tiempo : O (log N) para la entrada N dada porque se usa la función pow incorporada
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por SHUBHAMSINGH10 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA