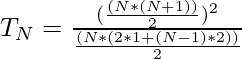Encuentre el término N de la serie 1^3/1+(1^3+2^3)/(1+3)+(1^3+2^3+3^3)/(1+3+5)+ …

Dado un entero positivo N . La tarea es encontrar el término N de la serie:

Ejemplos:

Entrada: N = 2
Salida: 2,25

Entrada: N = 3
Salida: 4

Acercarse:  

A partir de la serie dada, encuentre la fórmula para el término N :  

1er término = 1^3/1 = 1/1 = 1

2do término = (1^3+2^3)/(1+3) = (1+8)/4 = 9/4 = 2.25

3er término = (1^3+2^3+3^3)/(1+3+5) = (1+8+27)/9 = 4

4to término = (1^3+2^3+3^3+4^3)/(1+3+5+7) = (1+8+27+64)/16 = 6.25

.

.

N-ésimo término = ((N*(N+1)/2)^2)/(N*(2+(N-1)*2)/2) = (N+1)^2/4 = (N^ 2+2N+1)/4

Derivación:

Para la serie-

El enésimo término se puede escribir como-

Aquí,

 y 1+3+5+….+(2*N-1) están en AP

Reescribiendo la ecuación anterior usando la fórmula para AP as-

El término N de la serie dada se puede generalizar como:

Ilustración:

Entrada: N = 2
Salida: 2,25
Explicación: (1^3+2^3)/(1+3) 
                  = (1 +8)/4 
                  = 9/4 
                  = 2,25

A continuación se muestra la implementación del problema anterior:

// C++ program to find N-th term
// in the series
#include <bits/stdc++.h>
using namespace std;
 
// Function to find N-th term
// in the series
double nthTerm(int N)
{
    return (pow(N, 2) +
            2 * N + 1) / 4;
}
 
// Driver Code
int main()
{
    // Get the value of N
    int N = 5;
    cout << nthTerm(N);
    return 0;
}

// Java code for the above approach
import java.io.*;
class GFG {
 
    // Function to find N-th term
    // in the series
    static double nthTerm(int N)
    {
        return (Math.pow(N, 2) + 2 * N + 1) / 4;
    }
    public static void main(String[] args)
    {
        // Get the value of N
        int N = 5;
 
        System.out.println(nthTerm(N));
    }
}
 
// This code is contributed by Potta Lokesh

# python 3 program for the above approach
import sys
 
# Function to find N-th term
# in the series
def nthTerm(N):
 
    return (pow(N, 2) + 2 * N + 1) / 4
 
# Driver Code
if __name__ == "__main__":
       
     N = 5
     print(nthTerm(N))
 
    # This code is contributed by hrithikgarg03188

// C# program to find N-th term
// in the series
using System;
class GFG
{
 
  // Function to find N-th term
  // in the series
  static double nthTerm(int N)
  {
    return (Math.Pow(N, 2) +
            2 * N + 1) / 4;
  }
 
  // Driver Code
  public static void Main()
  {
 
    // Get the value of N
    int N = 5;
    Console.Write(nthTerm(N));
  }
}
 
// This code is contributed by Samim Hosdsain Mondal.

<script>
    // JavaScript program to find N-th term
    // in the series
 
    // Function to find N-th term
    // in the series
    const nthTerm = (N) => {
        return (Math.pow(N, 2) +
            2 * N + 1) / 4;
    }
 
    // Driver Code
 
    // Get the value of N
    let N = 5;
    document.write(nthTerm(N));
 
// This code is contributed by rakeshsahni
 
</script>

9

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)