Encuentra la longitud de la mediana de un triángulo si se dan las longitudes de los lados

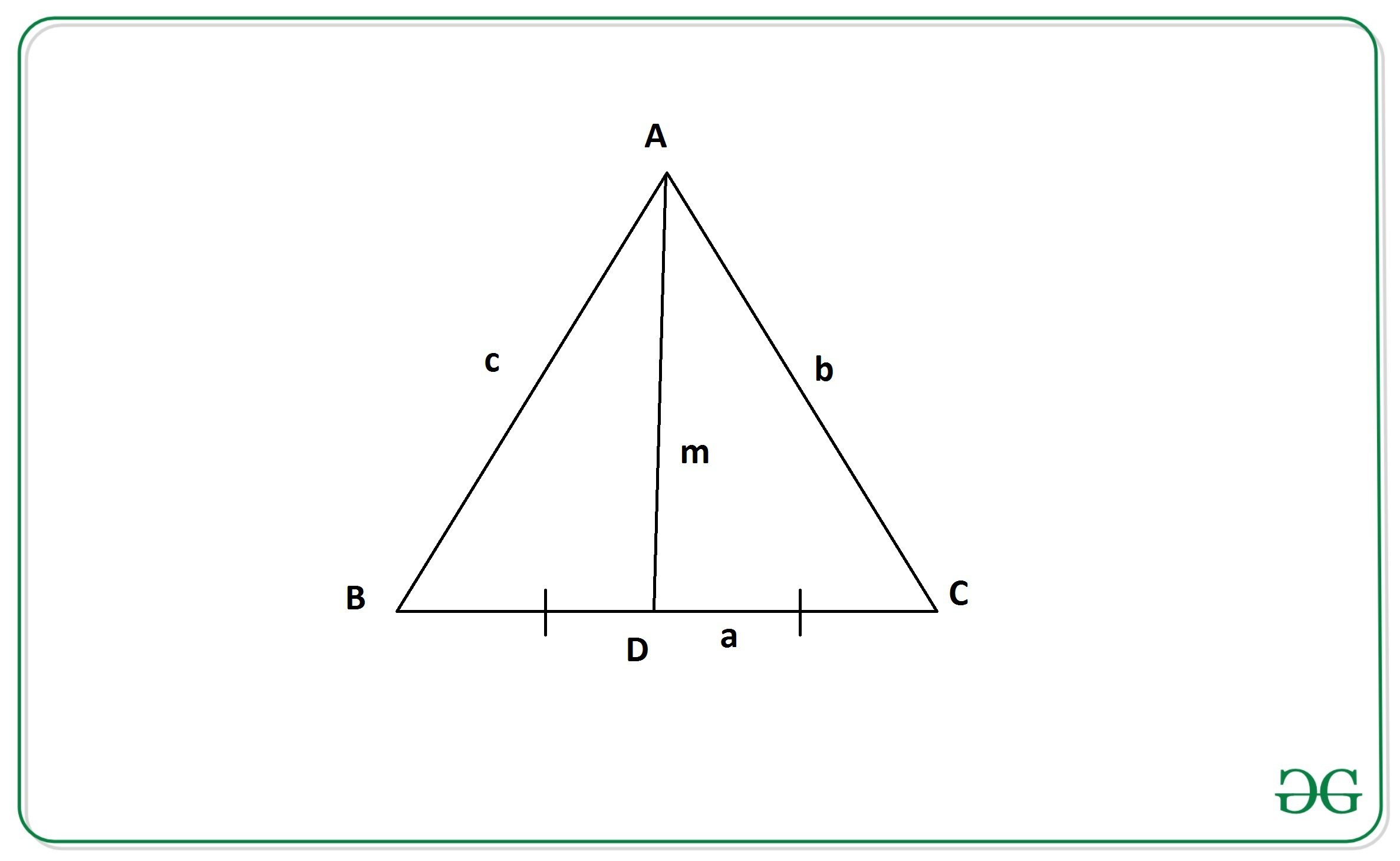
Dada la longitud de los tres lados de un triángulo como a , b y c . La tarea es calcular la longitud de la mediana del triángulo.
 

La mediana de un triángulo es un segmento de recta que une un vértice con el punto medio del lado opuesto, bisecando así ese lado. 
 

Ejemplos: 
 

Entrada: a = 8, b = 10, c = 13 
Salida: 10,89
Entrada: a = 4, b = 3, c = 5 
Salida: 3,61 
 

Enfoque: La idea es utilizar el teorema de Apolonio para resolver este problema.
 

El Teorema de Apolonio establece que “la suma de los cuadrados de dos lados cualesquiera de un triángulo es igual al doble del cuadrado de la mitad del tercer lado y al doble del cuadrado de la mediana que divide al tercer lado”.
 

De la figura anterior, de acuerdo con el Teorema de Apolonio tenemos: 
 

 

donde a, b y c son la longitud de los lados del triángulo 
y m es la longitud de la mediana del triángulo en el lado 2*a 
 

 

Por lo tanto, la longitud de la mediana de un triángulo de la ecuación anterior viene dada por: 
 

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find the length of the
// median using sides of the triangle
#include<bits/stdc++.h>
using namespace std;
 
// Function to return the length of
// the median using sides of triangle
float median(int a, int b, int c)
{
    float n = sqrt(2 * b * b +
                   2 * c * c - a * a) / 2;
    return n;
}
 
// Driver code
int main()
{
    int a, b, c;
    a = 4;
    b = 3;
    c = 5;
 
    // Function call
    float ans = median(a, b, c);
 
    // Print final answer with 2
    // digits after decimal
    cout << fixed << setprecision(2) << ans;
    return 0;
}
 
// This code is contributed by himanshu77

// Java program to find the length of the
// median using sides of the triangle
import java.util.*;
 
class GFG{
     
// Function to return the length of
// the median using sides of triangle
public static float median(int a, int b, int c)
{
    float n = (float)(Math.sqrt(2 * b * b +
                                2 * c * c -
                                a * a) / 2);
    return n;
}
 
// Driver code
public static void main(String[] args)
{
    int a, b, c;
    a = 4;
    b = 3;
    c = 5;
 
    // Function call
    float ans = median(a, b, c);
 
    // Print final answer with 2
    // digits after decimal
    System.out.println(String.format("%.2f", ans));
}
}
 
// This code is contributed by divyeshrabadiya07

# Python3 implementation to Find the
# length of the median using sides
# of the triangle
 
import math
 
# Function to return the length of
# the median using sides of triangle.
def median(a, b, c):
  
    n = (1 / 2)*math.sqrt(2*(b**2)
   + 2*(c**2)
 - a**2) 
 
    return n
 
# Driver Code
a = 4
b = 3
c = 5
 
# Function Call
ans = median(a, b, c)
 
# Print the final answer
print(round(ans, 2))

// C# program to find the length of the
// median using sides of the triangle
using System;
 
class GFG{
     
// Function to return the length of
// the median using sides of triangle
public static float median(int a, int b, int c)
{
    float n = (float)(Math.Sqrt(2 * b * b +
                                2 * c * c -
                                a * a) / 2);
    return n;
}
 
// Driver code
public static void Main(String[] args)
{
    int a, b, c;
    a = 4;
    b = 3;
    c = 5;
 
    // Function call
    float ans = median(a, b, c);
 
    // Print readonly answer with 2
    // digits after decimal
    Console.WriteLine(String.Format("{0:F2}", ans));
}
}
 
// This code is contributed by gauravrajput1

<script>
 
// JavaScript program to find the length of the
// median using sides of the triangle
 
// Function to return the length of
// the median using sides of triangle
function median(a, b, c)
{
    let n = (Math.sqrt(2 * b * b +
                                2 * c * c -
                                a * a) / 2);
    return n;
}
    
 
// Driver Code
 
     let a, b, c;
    a = 4;
    b = 3;
    c = 5;
   
    // Function call
    let ans = median(a, b, c);
   
    // Print final answer with 2
    // digits after decimal
    document.write(ans, 2);
           
</script>

3.61

Complejidad de tiempo: O(1) 
Complejidad de espacio: O(1)