Dada una array A, que consta de N enteros no negativos, encuentre la suma de xor de todos los tripletes desordenados de la array. Para tripletes no ordenados, el triplete (A[i], A[j], A[k]) se considera igual que los tripletes (A[j], A[i], A[k]) y todas las demás permutaciones.
Dado que la respuesta puede ser grande, calcule su mod a 10037.
Ejemplos:
Input : A = [3, 5, 2, 18, 7] Output : 132 Input : A = [140, 1, 66] Output : 207
Enfoque ingenuo
Iterar sobre todos los tripletes desordenados y sumar xor de cada uno a la suma.
Enfoque eficiente
- Un punto importante a observar es que xor es independiente de todos los bits. Entonces podemos hacer el cálculo requerido sobre cada bit individualmente.
- Consideremos el k-ésimo bit de todos los elementos del arreglo. Si el número de tripletes no ordenados es k’th bit xor 1 sea C, podemos simplemente agregar C * 2 k a la respuesta. Sea X el número de elementos cuyo k-ésimo bit es 1 y cuyo k-ésimo bit es 0 sea Y. Luego encuentre los tripletes desordenados cuyos k-ésimos bits xor a 1 se pueden formar usando dos casos:
- Solo uno de los tres elementos tiene k’ésimo bit 1.
- Los tres tienen k’ésimo bit 1.
- Número de formas de seleccionar 3 elementos que tienen k’th bit 1 =
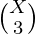
- Número de formas de seleccionar 1 elemento con k’th bit 1 y descansar con 0 =
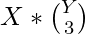
- Usaremos nCr mod p para calcular los valores de la función combinatoria.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to find sum of xor of
// all unordered triplets of the array
#include <bits/stdc++.h>
using namespace std;
// Iterative Function to calculate
// (x^y)%p in O(log y)
int power(int x, int y, int p)
{
// Initialize result
int res = 1;
// Update x if it is more than or
// equal to p
x = x % p;
while (y > 0)
{
// If y is odd, multiply x
// with result
if (y & 1)
res = (res * x) % p;
// y must be even now
y = y >> 1; // y = y/2
x = (x * x) % p;
}
return res;
}
// Returns n^(-1) mod p
int modInverse(int n, int p)
{
return power(n, p - 2, p);
}
// Returns nCr % p using Fermat's little
// theorem.
int nCrModPFermat(int n, int r, int p)
{
// Base case
if (r == 0)
return 1;
if (n < r)
return 0;
// Fill factorial array so that we
// can find all factorial of r, n
// and n-r
int fac[n + 1];
fac[0] = 1;
for (int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % p;
return (fac[n] * modInverse(fac[r], p) % p
* modInverse(fac[n - r], p) % p) % p;
}
// Function returns sum of xor of all
// unordered triplets of the array
int SumOfXor(int a[], int n)
{
int mod = 10037;
int answer = 0;
// Iterating over the bits
for (int k = 0; k < 32; k++)
{
// Number of elements whith k'th bit
// 1 and 0 respectively
int x = 0, y = 0;
for (int i = 0; i < n; i++)
{
// Checking if k'th bit is 1
if (a[i] & (1 << k))
x++;
else
y++;
}
// Adding this bit's part to the answer
answer += ((1 << k) % mod *
(nCrModPFermat(x, 3, mod)
+ x * nCrModPFermat(y, 2, mod))
% mod) % mod;
}
return answer;
}
// Drivers code
int main()
{
int n = 5;
int A[n] = { 3, 5, 2, 18, 7 };
cout << SumOfXor(A, n);
return 0;
}
Java
// Java program to find sum of xor of
// all unordered triplets of the array
class GFG{
// Iterative Function to calculate
// (x^y)%p in O(log y)
static int power(int x, int y, int p)
{
// Initialize result
int res = 1;
// Update x if it is more than or
// equal to p
x = x % p;
while (y > 0)
{
// If y is odd, multiply x
// with result
if ((y & 1) == 1)
res = (res * x) % p;
// y must be even now
y = y >> 1; // y = y/2
x = (x * x) % p;
}
return res;
}
// Returns n^(-1) mod p
static int modInverse(int n, int p)
{
return power(n, p - 2, p);
}
// Returns nCr % p using Fermat's little
// theorem.
static int nCrModPFermat(int n, int r, int p)
{
// Base case
if (r == 0)
return 1;
if (n < r)
return 0;
// Fill factorial array so that we
// can find all factorial of r, n
// and n-r
int fac[] = new int[n + 1];
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % p;
return (fac[n] * modInverse(fac[r], p) % p *
modInverse(fac[n - r], p) %
p) % p;
}
// Function returns sum of xor of all
// unordered triplets of the array
static int SumOfXor(int a[], int n)
{
int mod = 10037;
int answer = 0;
// Iterating over the bits
for(int k = 0; k < 32; k++)
{
// Number of elements whith k'th bit
// 1 and 0 respectively
int x = 0, y = 0;
for(int i = 0; i < n; i++)
{
// Checking if k'th bit is 1
if ((a[i] & (1 << k)) != 0)
x++;
else
y++;
}
// Adding this bit's part to the answer
answer += ((1 << k) % mod *
(nCrModPFermat(x, 3, mod) + x *
nCrModPFermat(y, 2, mod)) %
mod) % mod;
}
return answer;
}
// Driver code
public static void main(String[] args)
{
int n = 5;
int A[] = { 3, 5, 2, 18, 7 };
System.out.println(SumOfXor(A, n));
}
}
// This code is contributed by jrishabh99
Python3
# Python3 program to find sum of xor of # all unordered triplets of the array # Iterative Function to calculate # (x^y)%p in O(log y) def power(x, y, p): # Initialize result res = 1 # Update x if it is more than or # equal to p x = x % p while (y > 0): # If y is odd, multiply x # with result if (y & 1): res = (res * x) % p # y must be even now y = y >> 1#y = y/2 x = (x * x) % p return res # Returns n^(-1) mod p def modInverse(n, p): return power(n, p - 2, p) # Returns nCr % p using Fermat's little # theorem. def nCrModPFermat(n, r, p): # Base case if (r == 0): return 1 if (n < r): return 0 # Fill factorial array so that we # can find all factorial of r, n # and n-r fac = [0]*(n + 1) fac[0] = 1 for i in range(1, n + 1): fac[i] = fac[i - 1] * i % p return (fac[n] * modInverse(fac[r], p) % p * modInverse(fac[n - r], p) % p) % p # Function returns sum of xor of all # unordered triplets of the array def SumOfXor(a, n): mod = 10037 answer = 0 # Iterating over the bits for k in range(32): # Number of elements whith k'th bit # 1 and 0 respectively x = 0 y = 0 for i in range(n): # Checking if k'th bit is 1 if (a[i] & (1 << k)): x += 1 else: y += 1 # Adding this bit's part to the answer answer += ((1 << k) % mod * (nCrModPFermat(x, 3, mod) + x * nCrModPFermat(y, 2, mod)) % mod) % mod return answer # Drivers code if __name__ == '__main__': n = 5 A=[3, 5, 2, 18, 7] print(SumOfXor(A, n)) # This code is contributed by mohit kumar 29
C#
// C# program to find sum of xor of
// all unordered triplets of the array
using System;
class GFG{
// Iterative Function to calculate
// (x^y)%p in O(log y)
static int power(int x, int y, int p)
{
// Initialize result
int res = 1;
// Update x if it is more than or
// equal to p
x = x % p;
while (y > 0)
{
// If y is odd, multiply x
// with result
if ((y & 1) == 1)
res = (res * x) % p;
// y must be even now
y = y >> 1; // y = y/2
x = (x * x) % p;
}
return res;
}
// Returns n^(-1) mod p
static int modInverse(int n, int p)
{
return power(n, p - 2, p);
}
// Returns nCr % p using Fermat's little
// theorem.
static int nCrModPFermat(int n, int r, int p)
{
// Base case
if (r == 0)
return 1;
if (n < r)
return 0;
// Fill factorial array so that we
// can find all factorial of r, n
// and n-r
int []fac = new int[n + 1];
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % p;
return (fac[n] * modInverse(fac[r], p) % p *
modInverse(fac[n - r], p) %
p) % p;
}
// Function returns sum of xor of all
// unordered triplets of the array
static int SumOfXor(int []a, int n)
{
int mod = 10037;
int answer = 0;
// Iterating over the bits
for(int k = 0; k < 32; k++)
{
// Number of elements whith k'th bit
// 1 and 0 respectively
int x = 0, y = 0;
for(int i = 0; i < n; i++)
{
// Checking if k'th bit is 1
if ((a[i] & (1 << k)) != 0)
x++;
else
y++;
}
// Adding this bit's part to the answer
answer += ((1 << k) % mod *
(nCrModPFermat(x, 3, mod) + x *
nCrModPFermat(y, 2, mod)) %
mod) % mod;
}
return answer;
}
// Driver code
public static void Main(String[] args)
{
int n = 5;
int []A = { 3, 5, 2, 18, 7 };
Console.WriteLine(SumOfXor(A, n));
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// Javascript program to find sum of xor of
// all unordered triplets of the array
// Iterative Function to calculate
// (x^y)%p in O(log y)
function power(x, y, p)
{
// Initialize result
let res = 1;
// Update x if it is more than or
// equal to p
x = x % p;
while (y > 0)
{
// If y is odd, multiply x
// with result
if ((y & 1) == 1)
res = (res * x) % p;
// y must be even now
y = y >> 1; // y = y/2
x = (x * x) % p;
}
return res;
}
// Returns n^(-1) mod p
function modInverse(n, p)
{
return power(n, p - 2, p);
}
// Returns nCr % p using Fermat's little
// theorem.
function nCrModPFermat(n, r, p)
{
// Base case
if (r == 0)
return 1;
if (n < r)
return 0;
// Fill factorial array so that we
// can find all factorial of r, n
// and n-r
let fac = Array.from({length: n+1}, (_, i) => 0);
fac[0] = 1;
for(let i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % p;
return (fac[n] * modInverse(fac[r], p) % p *
modInverse(fac[n - r], p) %
p) % p;
}
// Function returns sum of xor of all
// unordered triplets of the array
function SumOfXor(a, n)
{
let mod = 10037;
let answer = 0;
// Iterating over the bits
for(let k = 0; k < 32; k++)
{
// Number of elements whith k'th bit
// 1 and 0 respectively
let x = 0, y = 0;
for(let i = 0; i < n; i++)
{
// Checking if k'th bit is 1
if ((a[i] & (1 << k)) != 0)
x++;
else
y++;
}
// Adding this bit's part to the answer
answer += ((1 << k) % mod *
(nCrModPFermat(x, 3, mod) + x *
nCrModPFermat(y, 2, mod)) %
mod) % mod;
}
return answer;
}
// Driver Code
let n = 5;
let A = [ 3, 5, 2, 18, 7 ];
document.write(SumOfXor(A, n));
</script>
Producción:
132
Complejidad de tiempo: O (32 * N)