Encuentre ln(X) y log10X con la ayuda de la expansión

Dado un número x positivo, la tarea es encontrar el logaritmo natural (ln) y logaritmo en base 10 (log ₁₀ ) de este número con la ayuda de la expansión.

Ejemplo:  

Input: x = 5
Output: ln 5.000 = 1.609
        log10 5.000 = 0.699

Input: x = 10
Output: ln 10.000 = 2.303
        log10 10.000 = 1.000

Acercarse:  

• La expansión del logaritmo natural de x (ln x) es:
   

• Por lo tanto, esta serie se puede resumir como: 
   

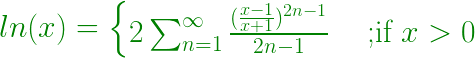
• Por lo tanto, se puede hacer una función para evaluar el enésimo término de la secuencia para 1 ≤ x ≤ n 
• Ahora, para calcular log ₁₀ x , se puede usar la siguiente fórmula: 
   

A continuación se muestra la implementación del enfoque anterior: 

// CPP code to Find the ln x and
// log<sub>10</sub> x with the help of expansion
 
#include <cmath>
#include <iomanip>
#include <iostream>
 
using namespace std;
 
// Function to calculate ln x using expansion
double calculateLnx(double n)
{
 
    double num, mul, cal, sum = 0;
    num = (n - 1) / (n + 1);
 
    // terminating value of the loop
    // can be increased to improve the precision
    for (int i = 1; i <= 1000; i++) {
        mul = (2 * i) - 1;
        cal = pow(num, mul);
        cal = cal / mul;
        sum = sum + cal;
    }
    sum = 2 * sum;
    return sum;
}
 
// Function to calculate log10 x
double calculateLogx(double lnx)
{
    return (lnx / 2.303);
}
 
// Driver Code
int main()
{
 
    double lnx, logx, n = 5;
    lnx = calculateLnx(n);
    logx = calculateLogx(lnx);
 
    // setprecision(3) is used to display
    // the output up to 3 decimal places
 
    cout << fixed << setprecision(3)
         << "ln " << n << " = "
         << lnx << endl;
    cout << fixed << setprecision(3)
         << "log10 " << n << " = "
         << logx << endl;
}

// Java code to Find the ln x and
// log<sub>10</sub> x with the help of expansion
import java.io.*;
 
class GFG
{
     
// Function to calculate ln x using expansion
static double calculateLnx(double n)
{
    double num, mul, cal, sum = 0;
    num = (n - 1) / (n + 1);
 
    // terminating value of the loop
    // can be increased to improve the precision
    for (int i = 1; i <= 1000; i++)
    {
        mul = (2 * i) - 1;
        cal = Math.pow(num, mul);
        cal = cal / mul;
        sum = sum + cal;
    }
    sum = 2 * sum;
    return sum;
}
 
// Function to calculate log10 x
static double calculateLogx(double lnx)
{
    return (lnx / 2.303);
}
 
// Driver Code
public static void main (String[] args)
{
    double lnx, logx, n = 5;
    lnx = calculateLnx(n);
    logx = calculateLogx(lnx);
     
    // setprecision(3) is used to display
    // the output up to 3 decimal places
     
    System.out.println ("ln " + n + " = " + lnx );
    System.out.println ("log10 " + n + " = "+ logx );
}
}
 
// This code is contributed by ajit

# Python 3 code to Find the ln x and
# log<sub>10</sub> x with the help of expansion
# Function to calculate ln x using expansion
from math import pow
def calculateLnx(n):
    sum = 0
    num = (n - 1) / (n + 1)
 
    # terminating value of the loop
    # can be increased to improve the precision
    for i in range(1, 1001, 1):
        mul = (2 * i) - 1
        cal = pow(num, mul)
        cal = cal / mul
        sum = sum + cal
 
    sum = 2 * sum
    return sum
 
# Function to calculate log10 x
def calculateLogx(lnx):
    return (lnx / 2.303)
 
# Driver Code
if __name__ == '__main__':
    n = 5
    lnx = calculateLnx(n)
    logx = calculateLogx(lnx)
 
    # setprecision(3) is used to display
    # the output up to 3 decimal places
 
    print("ln", "{0:.3f}".format(n),
           "=", "{0:.3f}".format(lnx))
    print("log10", "{0:.3f}".format(n),
              "=", "{0:.3f}".format(logx))
     
# This code is contributed by
# Surendra_Gangwar

// C# code to Find the ln x and
// log<sub>10</sub> x with the help of expansion
using System;
     
class GFG
{
     
// Function to calculate ln x using expansion
static double calculateLnx(double n)
{
    double num, mul, cal, sum = 0;
    num = (n - 1) / (n + 1);
 
    // terminating value of the loop
    // can be increased to improve the precision
    for (int i = 1; i <= 1000; i++)
    {
        mul = (2 * i) - 1;
        cal = Math.Pow(num, mul);
        cal = cal / mul;
        sum = sum + cal;
    }
    sum = 2 * sum;
    return sum;
}
 
// Function to calculate log10 x
static double calculateLogx(double lnx)
{
    return (lnx / 2.303);
}
 
// Driver Code
public static void Main (String[] args)
{
    double lnx, logx, n = 5;
    lnx = calculateLnx(n);
    logx = calculateLogx(lnx);
     
    // setprecision(3) is used to display
    // the output up to 3 decimal places
     
    Console.WriteLine("ln " + n + " = " + lnx );
    Console.WriteLine("log10 " + n + " = "+ logx );
}
}
 
// This code is contributed by Princi Singh

<script>
 
// Javascript code to Find the ln x and
// log<sub>10</sub> x with the help of expansion
 
// Function to calculate ln x using expansion
function calculateLnx(n)
{
    let num, mul, cal, sum = 0;
    num = (n - 1) / (n + 1);
 
    // Terminating value of the loop
    // can be increased to improve the precision
    for(let i = 1; i <= 1000; i++)
    {
        mul = (2 * i) - 1;
        cal = Math.pow(num, mul);
        cal = cal / mul;
        sum = sum + cal;
    }
    sum = 2 * sum;
    return sum;
}
 
// Function to calculate log10 x
function calculateLogx(lnx)
{
    return (lnx / 2.303);
}
 
// Driver Code
let lnx, logx, n = 5;
lnx = calculateLnx(n);
logx = calculateLogx(lnx);
 
// setprecision(3) is used to display
// the output up to 3 decimal places
document.write("ln " + n + " = " + lnx + "<br>");
document.write("log10 " + n + " = "+ logx + "<br>");
 
// This code is contributed by souravmahato348
 
</script>

ln 5.000 = 1.609
log10 5.000 = 0.699