Encuentre una permutación de 2N números tal que el resultado de la expresión dada sea exactamente 2K

Dados dos números enteros N y K , la tarea es encontrar una permutación de los primeros 2*N números naturales tal que se satisfaga la siguiente ecuación.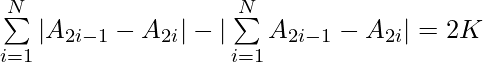 

Nota: El valor de K siempre será menor o igual que N.
Ejemplos: 
 

Input : N = 1,  K = 0
Output : 1 2
The result of the above expression will be:
|1-2|-|1-2| =0

Input : N = 2,  K = 1 
Output : 2 1 3 4
The result of the above expression will be:
(|2-1|+|3-4|)-(|2-1+3-4|) = 2

Enfoque:
considere la permutación ordenada: 
 

1, 2, 3, 4, 5, 6.... 

El resultado de la expresión será exactamente 0. Si intercambiamos 2 índices cualesquiera 2i-1 y 2i , el resultado aumentará exactamente en 2. Por lo tanto, necesitamos hacer K tales intercambios. 
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find the required permutation
// of first 2*N natural numbers
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the required permutation
// of first 2*N natural numbers
void printPermutation(int n, int k)
{
    // Iterate in blocks of 2
    for (int i = 1; i <= n; i++) {
        int x = 2 * i - 1;
        int y = 2 * i;
 
        // We need more increments, so print in reverse order
        if (i <= k)
            cout << y << " " << x << " ";
 
        // We have enough increments, so print in same order
        else
            cout << x << " " << y << " ";
    }
}
 
// Driver Code
int main()
{
    int n = 2, k = 1;
 
    printPermutation(n, k);
 
    return 0;
}

// Java program to find the
// required permutation
// of first 2*N natural numbers
class GFG
{
         
    // Function to find the required permutation
    // of first 2*N natural numbers
    static void printPermutation(int n, int k)
    {
        // Iterate in blocks of 2
        for (int i = 1; i <= n; i++)
        {
            int x = 2 * i - 1;
            int y = 2 * i;
         
        // We need more increments,
        // so print in reverse order
        if (i <= k)
            System.out.print(y + " " + x + " ");
 
        // We have enough increments,
        // so print in same order
        else
            System.out.print(x + " " + y + " ");
        }
    }
         
    // Driver code
    public static void main(String []args)
    {
        int n = 2, k = 1;
        printPermutation(n, k);
    }
}
 
// This code is contributed by Ita_c.

# Python3 program to find the required
# permutation of first 2*N natural numbers
 
# Function to find the required permutation
# of first 2*N natural numbers
def printPermutation(n, k) :
     
    # Iterate in blocks of 2
    for i in range(1, n + 1) :
        x = 2 * i - 1;
        y = 2 * i;
 
        # We need more increments,
        # so print in reverse order
        if (i <= k) :
            print(y, x, end = " ");
 
        # We have enough increments,
        # so print in same order
        else :
            print(x, y, end = " ");
 
# Driver Code
if __name__ == "__main__" :
    n = 2; k = 1;
 
    printPermutation(n, k);
     
# This code is contributed by Ryuga

using System;
 
// C# program to find the
// required permutation
// of first 2*N natural numbers
     
class GFG
{
         
    // Function to find the required permutation
    // of first 2*N natural numbers
    static void printPermutation(int n, int k)
    {
        // Iterate in blocks of 2
        for (int i = 1; i <= n; i++)
        {
            int x = 2 * i - 1;
            int y = 2 * i;
         
        // We need more increments,
        // so print in reverse order
        if (i <= k)
            Console.Write(y + " " + x + " ");
 
        // We have enough increments,
        // so print in same order
        else
            Console.Write(x + " " + y + " ");
        }
    }
         
    // Driver code
    public static void Main()
    {
        int n = 2, k = 1;
        printPermutation(n, k);
    }
}
 
// This code is contributed by
// shashank_sharma

<?php
// PHP program to find the required
// permutation of first 2*N natural numbers
 
// Function to find the required permutation
// of first 2*N natural numbers
function printPermutation($n, $k)
{
    // Iterate in blocks of 2
    for ($i = 1; $i <= $n; $i++)
    {
        $x = 2 * $i - 1;
        $y = 2 * $i;
 
        // We need more increments, so print
        // in reverse order
        if ($i <= $k)
            echo $y . " " . $x . " ";
 
        // We have enough increments,
        // so print in same order
        else
            echo $x . " " . $y . " ";
    }
}
 
// Driver Code
$n = 2;
$k = 1;
 
printPermutation($n, $k);
 
// This code is contributed by chandan_jnu
?>

<script>
 
// javascript program to find the
// required permutation
// of first 2*N natural numbers
     
  
         
    // Function to find the required permutation
    // of first 2*N natural numbers
    function printPermutation( n,  k)
    {
        // Iterate in blocks of 2
        for (var i = 1; i <= n; i++)
        {
            var x = 2 * i - 1;
            var y = 2 * i;
         
        // We need more increments,
        // so print in reverse order
        if (i <= k)
            document.write(y + " " + x + " ");
 
        // We have enough increments,
        // so print in same order
        else
            document.write(x + " " + y + " ");
        }
    }
         
    // Driver code
  
        var n = 2, k = 1;
        printPermutation(n, k);
         
        // This code is contributed by bunnyram19.
         
</script>

2 1 3 4

Complejidad Temporal: O(N), ya que allí corre un bucle de 1 a n.
Espacio Auxiliar : O(1), ya que no se ha tomado ningún espacio extra.