Error verdadero frente a error de muestra

verdadero error

El verdadero error se puede decir como la probabilidad de que la hipótesis clasifique erróneamente una sola muestra extraída al azar de la población. Aquí la población representa todos los datos del mundo.

Consideremos una hipótesis h(x) y la función verdadero/objetivo es f(x) de la población P. La probabilidad de que h clasifique erróneamente una instancia extraída al azar, es decir, el error verdadero es:

$T.E. = Prob[f(x) \neq h(x)]$

Error de muestra

El error de muestra de S con respecto a la función objetivo f y la muestra de datos S es la proporción de ejemplos que S clasifica incorrectamente.

$S.E. =\frac{1}{n} \sum_{x \epsilon S}\delta(f(x) \neq h(x))$

$Sample \, Error = \frac{Number\, of\, missclassified \, instances}{Total \, Number \, of \, Instance}$

o, la siguiente fórmula representa también representa un error de muestra:

$S.E. = \frac{FP + FN}{TP + FP + FN + TN}$
$S.E. = 1 - \frac{TP + TN}{TP + FP + FN + TN}$
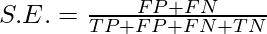
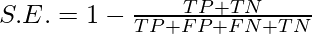
SE = 1- Precisión

Suponga que la Hipótesis h clasifica incorrectamente los 7 de los 33 ejemplos en poblaciones totales. Entonces el error de muestreo debe ser:

$SE = \frac{7}{33} = .21$

Sesgo y varianza

Sesgo : el sesgo es la diferencia entre la predicción promedio de la hipótesis y el valor correcto de la predicción. La hipótesis con alto sesgo intenta simplificar demasiado el entrenamiento (no trabajar sobre un modelo complejo). Tiende a tener altos errores de entrenamiento y altos errores de prueba.

$Bias = E[h(x)]- f(x)$

Varianza: Las hipótesis de alta varianza tienen una alta variabilidad entre sus predicciones. Intentan sobrecomplejar el modelo y no generalizan muy bien los datos.

$Var(X) = E[(X - E[X])^2]$

Intervalo de confianza

Generalmente, el verdadero error es complejo y difícil de calcular. Se puede estimar con la ayuda de un intervalo de confianza. El intervalo de confianza se puede estimar como la función del error de muestreo.

A continuación se muestran los pasos para el intervalo de confianza:

Extraídas aleatoriamente n muestras S (independientemente unas de otras), donde n debería ser >30 de la población P.
Calcule el error de muestra de la muestra S.

Aquí asumimos que el error de muestreo es el estimador insesgado de True Error. La siguiente es la fórmula para calcular el error verdadero:

$T.E. = S.E. \pm z_{s} \sqrt{\frac{S.E. (1- S.E.)}{n}}$

donde z _s es el valor de la puntuación z del porcentaje s del intervalo de confianza:

% Intervalo de confianza	50	80	90	95	99	99.5
puntuación Z	0,67	1.28	1.64	1.96	2.58	2.80