Funciones de costo de entropía cruzada utilizadas en la clasificación

Una breve idea de las funciones de costo

¿Cómo valora tu profesor si has estudiado durante todo el curso académico o no? Ella toma una prueba al final y califica su desempeño al cotejar sus respuestas con las respuestas deseadas. Si ha logrado mantener su precisión y ha disparado sus puntajes por encima de un cierto punto de referencia, ha pasado. Si no lo ha hecho (por improbable que sea), necesita mejorar su precisión e intentarlo de nuevo. Entonces, en palabras crudas, las pruebas se usan para analizar qué tan bien te has desempeñado en clase.

En la jerga del aprendizaje automático, se utiliza una ‘ función de costo ‘ para evaluar el rendimiento de un modelo. Una pregunta importante que podría surgir es, ¿cómo puedo evaluar el rendimiento de mi modelo ? Al igual que el maestro evalúa su precisión al verificar sus respuestas con las respuestas deseadas, usted evalúa la precisión del modelo al comparar los valores predichos por el modelo con los valores reales. La función de costo cuantifica la diferencia entre el valor real y el valor pronosticado y lo almacena como un número real de un solo valor. La función de costo puede llamarse análogamente la ‘ función de pérdida ‘‘ si se considera el error en un solo ejemplo de entrenamiento. Tenga en cuenta que estos son aplicables solo en algoritmos de aprendizaje automático supervisado que aprovechan las técnicas de optimización. Dado que la función de costo es la medida de cuánto se desvían nuestros valores predichos de los valores etiquetados correctos, se puede considerar que es una métrica inadecuada. Por lo tanto, todas las técnicas de optimización tienden a esforzarse por minimizarlo.

En este artículo, cubriremos las funciones de costo utilizadas predominantemente en modelos de clasificación únicamente.

La función de costo de entropía cruzada

La idea detrás de las entropías de Shannon

La entropía de una variable aleatoria X se puede medir como la incertidumbre en los posibles resultados de las variables. Esto significa que cuanto mayor es la certeza/probabilidad, menor es la entropía.

La fórmula para calcular la entropía se puede representar como:

$\begin{equation*} H(x)=-\int_{x} 1 . p(x) \log p(x), \text { if } X \text { is continuous } \end{equation*}$

$\begin{equation*} H(x)=\sum_{x} p(x) \log p(x) \text {, if } X \text { is discrete } \end{equation*}$

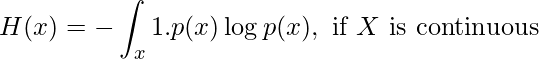
Tomemos un ejemplo sencillo.

Tienes 3 cestas y cada una de ellas contiene 10 caramelos.

El primer cesto tiene 3 Eclairs y 7 Alpenliebes.

Rojo = Eclairs, amarillo = Alpenliebe

El segundo cesto tiene 5 Eclairs y 5 Alpenliebes.

El tercer cesto tiene 10 Eclairs y 0 Alpenliebes.

Usando la ecuación anterior, podemos calcular los valores de las entropías en cada uno de los casos anteriores.

Ahora puede ver que dado que el cesto 2 tiene el mayor grado de incertidumbre, su entropía es el valor más alto posible, es decir, 1. Además, dado que el cesto 3 solo tiene un tipo de dulces, hay un 100% de certeza de que el dulce extraído sería un Éclair. Por lo tanto, no hay incertidumbre y la entropía es 0.

La función de costo de la entropía cruzada

Ahora que está familiarizado con la entropía, profundicemos en la función de costo de la entropía cruzada.

Tomemos un ejemplo de un problema de clasificación de 3 clases. El modelo aceptará una imagen y distinguirá si la imagen se puede clasificar como la de una manzana, una naranja o un mango. Después del procesamiento, el modelo proporcionaría una salida en forma de distribución de probabilidad. La clase predicha tendría la mayor probabilidad.

manzana = [1,0,0]
Naranja = [0,1,0]
Mango = [0,0,1]

Esto significa que si la clase predicha correctamente por el modelo es, digamos, manzana. Entonces, la distribución de probabilidad pronosticada de manzana debería tender hacia el valor máximo de distribución de probabilidad, es decir, 1. Si ese no es el caso, el peso del modelo necesita un ajuste.

Digamos que los siguientes logits fueron los valores predichos:

Logits para manzana, naranja y mango respectivamente

Estos son los valores logit respectivos para que la imagen de entrada sea una manzana, una naranja y un mango. Podemos implementar una función Softmax para convertir estos logits en probabilidades. La razón por la que usamos softmax es que es una función continuamente diferenciable. Esto hace posible calcular la derivada de la función de costo para cada peso en la red neuronal.

Diferencia entre el valor esperado y el valor predicho, es decir, 1 y 0,723 = 0,277

Aunque la probabilidad de manzana no es exactamente 1, está más cerca de 1 que todas las demás opciones.

Después de un entrenamiento iterativo sucesivo y posterior, el modelo podría mejorar considerablemente su probabilidad de salida y reducir la pérdida. Así es como la entropía cruzada puede reducir la función de costo y hacer que el modelo sea más preciso. La fórmula utilizada para predecir la función de costo es:

$\begin{equation*} L=-\sum_{i=1}^{n} y \log \left(p_{i}\right), \text { for } n \text { classes } \end{equation*}$

Funciones de costos de clasificación multiclase

Al igual que el ejemplo mencionado anteriormente, la clasificación de clases múltiples es el escenario en el que hay varias clases, pero la entrada se ajusta solo a 1 clase. La fruta no puede ser prácticamente un mango y una naranja a la vez, ¿verdad?

Deje que la salida del modelo resalte la distribución de probabilidad para las clases ‘ c’ para una entrada fija ‘d ‘.

$\begin{equation*} p(d)=\left[\begin{array}{c} p 1 \\ p 2 \\ p c \end{array}\right] \end{equation*}$

Además, sea la distribución de probabilidad real

$\begin{equation*} \mathrm{y}(\mathrm{d})=\left[\begin{array}{l} \mathrm{y} 1 \\ \mathrm{y} 2 \\ \mathrm{y} 3 \end{array}\right] \end{equation*}$

Por lo tanto, la función de costo de entropía cruzada se puede representar como:

Tenga en cuenta que y3=yc para todos los términos ‘c’

$-(y1 log(p1) + y2 log(p2) + ……yc log(pc) )$

Ahora, si tomamos el ejemplo de la distribución de probabilidad del ejemplo de manzanas, naranjas y mangos y sustituimos los valores en la fórmula, obtenemos:

p(manzana)=[0,723, 0,240, 0,036]
y(manzana)=[1,0,0]

Pérdida de entropía cruzada (y, P) = – (1*log(0,723) + 0*log(0,240)+0*log(0,036)) = 0,14

Este es el valor de la pérdida de entropía cruzada.

Entropía cruzada categórica

El error de clasificación del modelo completo viene dado por la media de la entropía cruzada del conjunto de datos de entrenamiento completo. Esta es la entropía cruzada categórica. La entropía cruzada categórica se utiliza cuando las etiquetas de valor real están codificadas en caliente. Esto significa que solo un ‘bit’ de datos es verdadero a la vez, como [1,0,0], [0,1,0] o [0,0,1]. La entropía cruzada categórica se puede representar matemáticamente como:

Entropía cruzada categórica = (Suma de la entropía cruzada para N datos)/N

Función de costo de entropía cruzada binaria

En la entropía cruzada binaria también, solo hay una salida posible. Esta salida puede tener valores discretos, ya sea 0 o 1. Por ejemplo, permita que la entrada de la imagen de una fruta en particular sea la de una manzana o la de una naranja. Ahora, reescribamos esta oración: Una fruta es una manzana o no es una manzana. Solo hay posibles salidas binarias, verdadero-falso .

Supongamos que la salida real se representa como una variable y

ahora, la entropía cruzada para un dato particular ‘d’ se puede simplificar como

Entropía cruzada(d) = – y*log(p) cuando y = 1
Entropía cruzada (d) = – (1-y)*log(1-p) cuando y = 0

La implementación del problema para este método es la misma que la de las funciones de costo multiclase. La diferencia es que solo se pueden aceptar clases binarias.

Entropía cruzada categórica dispersa

En la entropía cruzada categórica dispersa, las etiquetas de verdad se etiquetan con valores integrales. Por ejemplo, si se tiene en cuenta un problema de 3 clases, las etiquetas se codificarían como [1], [2], [3].

Tenga en cuenta que las funciones de costo de entropía cruzada binaria, la entropía cruzada categórica y la entropía cruzada categórica escasa se proporcionan con la API de Keras.

Publicación traducida automáticamente

Artículo escrito por ssanya0904 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA