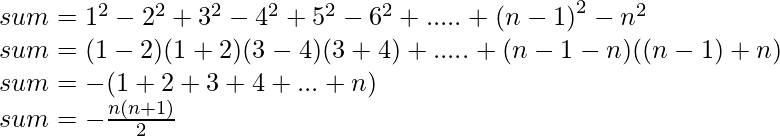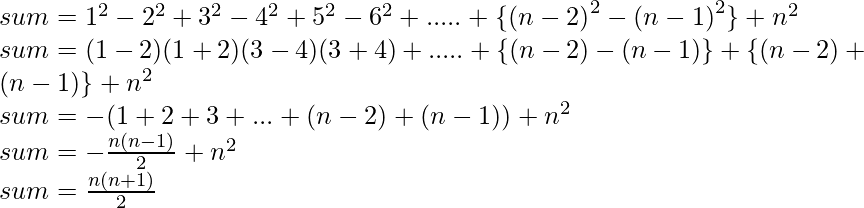Encuentre la suma de la serie 1 ^ 2 – 2 ^ 2 + 3 ^ 2 – 4 ^ 2 … .. hasta n términos

Posted on by Rudeus Greyrat

Dado un número n, la tarea es encontrar la suma de las siguientes series hasta n términos:
 

1 2 – 2 2 + 3 2 – 4 2 + …..

Ejemplos: 
 

Input: n = 2
Output: -3
Explanation: 
    sum = 12 - 22
    = 1 - 4
    = -3

Input: n = 3
Output: 6
Explanation: 
    sum = 12 - 22 + 32
    = 1 - 4 + 9
    = 6

Enfoque ingenuo:

Este método implica simplemente ejecutar un ciclo de i de 1 a n y si i es impar, simplemente agregue su cuadrado al resultado, si es par, luego simplemente reste el cuadrado al resultado.
A continuación se muestra la implementación del enfoque anterior:
 

C++

// C++ program to find sum of series
// 1^2 - 2^2 + 3^3 - 4^4 + ...
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find sum of series
int sum_of_series(int n)
{
    int result = 0;
    for (int i = 1; i <= n; i++) {
 
        // If i is even
        if (i % 2 == 0)
            result = result - pow(i, 2);
 
        // If i is odd
        else
            result = result + pow(i, 2);
    }
 
    // return the result
    return result;
}
 
// Driver Code
int main(void)
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    cout << sum_of_series(n) << endl;
 
    // Get n
    n = 10;
 
    // Find the sum
    cout << sum_of_series(n) << endl;
}

Java

// Java Program to find sum of series
// 1^2 - 2^2 + 3^3 - 4^4 + ...
import java.util.*;
import java.lang.*;
 
class GFG
{
// Function to find sum of series
static int sum_of_series(int n)
{
    int result = 0;
    for (int i = 1; i <= n; i++)
    {
 
        // If i is even
        if (i % 2 == 0)
            result = result -
                    (int)Math.pow(i, 2);
 
        // If i is odd
        else
            result = result +
                    (int)Math.pow(i, 2);
    }
 
    // return the result
    return result;
}
 
// Driver Code
public static void main(String args[])
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    System.out.println(sum_of_series(n));
 
    // Get n
    n = 10;
 
    // Find the sum
    System.out.println(sum_of_series(n));
}
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

Python3

# Python3 program to find sum of series
# 1^2 - 2^2 + 3^3 - 4^4 + ...
 
# Function to find sum of series
def sum_of_series(n):
 
    result = 0
    for i in range(1, n + 1) :
 
        # If i is even
        if (i % 2 == 0):
            result = result - pow(i, 2)
 
        # If i is odd
        else:
            result = result + pow(i, 2)
 
    # return the result
    return result
 
# Driver Code
if __name__ == "__main__":
 
    # Get n
    n = 3
 
    # Find the sum
    print(sum_of_series(n))
 
    # Get n
    n = 10
 
    # Find the sum
    print(sum_of_series(n))
 
# This code is contributed
# by ChitraNayal

C#

// C# Program to find sum of series
// 1^2 - 2^2 + 3^3 - 4^4 + ...
using System;
 
class GFG
{
// Function to find sum of series
static int sum_of_series(int n)
{
    int result = 0;
    for (int i = 1; i <= n; i++)
    {
 
        // If i is even
        if (i % 2 == 0)
            result = result -
                    (int)Math.Pow(i, 2);
 
        // If i is odd
        else
            result = result +
                    (int)Math.Pow(i, 2);
    }
 
    // return the result
    return result;
}
 
// Driver Code
public static void Main()
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    Console.WriteLine(sum_of_series(n));
 
    // Get n
    n = 10;
 
    // Find the sum
    Console.WriteLine(sum_of_series(n));
}
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

PHP

<?php
// PHP program to find sum of series
// 1^2 - 2^2 + 3^3 - 4^4 + ...
// Function to find sum of series
function sum_of_series($n)
{
    $result = 0;
    for ($i = 1; $i <= $n; $i++)
    {
 
        // If i is even
        if ($i % 2 == 0)
            $result = $result - pow($i, 2);
 
        // If i is odd
        else
            $result = $result + pow($i, 2);
    }
 
    // return the result
    return $result;
}
 
// Driver Code
 
// Get n
$n = 3;
 
// Find the sum
echo sum_of_series($n),"\n";
 
// Get n
$n = 10;
 
// Find the sum
echo sum_of_series($n),"\n";
 
// This Code is Contributed by anuj_67
?>

Javascript

<script>
 
// javascript Program to find sum of series
// 1^2 - 2^2 + 3^3 - 4^4 + ...
 
// Function to find sum of series
function sum_of_series(n)
{
    var result = 0;
    for (i = 1; i <= n; i++)
    {
 
        // If i is even
        if (i % 2 == 0)
            result = result -
                    parseInt(Math.pow(i, 2));
 
        // If i is odd
        else
            result = result +
                    parseInt(Math.pow(i, 2));
    }
 
    // return the result
    return result;
}
 
// Driver Code  
 
// Get n
var n = 3;
 
// Find the sum
document.write(sum_of_series(n)+ "<br>");
 
// Get n
n = 10;
 
// Find the sum
document.write(sum_of_series(n));
 
// This code is contributed by 29AjayKumar
 
</script>
Producción: 

6
-55

 

 Complejidad de tiempo: O (nlogn)

Espacio Auxiliar: O(1)

Enfoque eficiente

Se basa en la condición de n 
Si n es par:
 

sum = 1^2 - 2^2 + 3^2 - 4^2 + 5^2 - 6^2 + ..... + {(n-1)}^2 - n^2 \\ sum = (1 - 2 )( 1 + 2 )( 3 - 4 )( 3 + 4 )+ .....+ ( n - 1 - n)(( n - 1 ) + n ) \\ sum = -( 1 + 2 + 3 + 4 + ... + n ) \\ sum = -\frac{n ( n + 1 )}{2} \\

Si n es impar: 
 

sum = 1^2 - 2^2 + 3^2 - 4^2 + 5^2 - 6^2 + ..... + \{{(n-2)}^2 - {(n-1)}^2\} + n^2 \\ sum = (1 - 2 )( 1 + 2 )( 3 - 4 )( 3 + 4 )+ .....+ \{ ( n - 2 ) - ( n - 1)\} + \{ ( n - 2 ) + ( n - 1)\} + n^2 \\ sum = -( 1 + 2 + 3 + . . .+ (n - 2) + ( n -1 ) ) + n^2 \\ sum = -\frac{n ( n - 1 )}{2} + n^2 \\ sum = \frac{n ( n + 1 )}{2}

A continuación se muestra la implementación del enfoque anterior: 
 

C++

// C++ Program to find sum of series
// 1^2 - 2^2 +3^3 -4^4 + ...
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find sum of series
int sum_of_series(int n)
{
    int result = 0;
 
    // If n is even
    if (n % 2 == 0) {
        result = -(n * (n + 1)) / 2;
    }
 
    // If n is odd
    else {
        result = (n * (n + 1)) / 2;
    }
 
    // return the result
    return result;
}
 
// Driver Code
int main(void)
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    cout << sum_of_series(n) << endl;
 
    // Get n
    n = 10;
 
    // Find the sum
    cout << sum_of_series(n) << endl;
}

Java

// Java Program to find sum of series
// 1^2 - 2^2 +3^3 -4^4 + ...
import java.util.*;
import java.lang.*;
 
class GFG
{
// Function to find sum of series
static int sum_of_series(int n)
{
    int result = 0;
 
    // If n is even
    if (n % 2 == 0)
    {
        result = -(n * (n + 1)) / 2;
    }
 
    // If n is odd
    else
    {
        result = (n * (n + 1)) / 2;
    }
 
    // return the result
    return result;
}
 
// Driver Code
public static void main(String args[])
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    System.out.println(sum_of_series(n));
 
    // Get n
    n = 10;
 
    // Find the sum
    System.out.println(sum_of_series(n));
}
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

Python3

# Python3 Program to find sum of series
# 1^2 - 2^2 +3^3 -4^4 + ...
 
# Function to find sum of series
def sum_of_series(n) :
 
    result = 0
 
    # If n is even
    if (n % 2 == 0) :
        result = -(n * (n + 1)) // 2
     
    # If n is odd
    else :
        result = (n * (n + 1)) // 2
     
    # return the result
    return result
 
# Driver Code
if __name__ == "__main__" :
 
    # Get n
    n = 3
 
    # Find the sum
    print(sum_of_series(n))
 
    # Get n
    n = 10
 
    # Find the sum
    print(sum_of_series(n))
 
# This code is contributed by Ryuga

C#

// C# Program to find sum of series
// 1^2 - 2^2 +3^3 -4^4 + ...
 
using System;
 
class GFG
{
// Function to find sum of series
static int sum_of_series(int n)
{
    int result = 0;
 
    // If n is even
    if (n % 2 == 0)
    {
        result = -(n * (n + 1)) / 2;
    }
 
    // If n is odd
    else
    {
        result = (n * (n + 1)) / 2;
    }
 
    // return the result
    return result;
}
 
// Driver Code
public static void Main()
{
 
    // Get n
    int n = 3;
 
    // Find the sum
    Console.WriteLine(sum_of_series(n));
 
    // Get n
    n = 10;
 
    // Find the sum
    Console.WriteLine(sum_of_series(n));
}
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

PHP

<?php
// PHP program to find sum of series
// 1^2 - 2^2 +3^3 -4^4 + ...
 
// Function to find sum of series
function sum_of_series($n)
{
    $result = 0;
 
    // If n is even
    if ($n % 2 == 0)
    {
        $result = -($n * ($n + 1)) / 2;
    }
 
    // If n is odd
    else
    {
        $result = ($n * ($n + 1)) / 2;
    }
 
    // return the result
    return $result;
}
 
// Driver Code
 
// Get n
$n = 3;
 
// Find the sum
echo sum_of_series($n);
echo ("\n");
 
// Get n
$n = 10;
 
// Find the sum
echo sum_of_series($n);
echo ("\n");
 
// Get n
$n = 10;
 
// This code is contributed
// by Shivi_Aggarwal
?>

Javascript

<script>
// Javascript Program to find sum of series
// 1^2 - 2^2 +3^3 -4^4 + ...
 
 
 
    // Function to find sum of series
    function sum_of_series( n) {
        let result = 0;
 
        // If n is even
        if (n % 2 == 0) {
            result = -(n * (n + 1)) / 2;
        }
 
        // If n is odd
        else {
            result = (n * (n + 1)) / 2;
        }
 
        // return the result
        return result;
    }
 
    // Driver Code
      
 
        // Get n
        let n = 3;
 
        // Find the sum
        document.write(sum_of_series(n)+"<br/>");
 
        // Get n
        n = 10;
 
        // Find the sum
        document.write(sum_of_series(n));
 
// This code is contributed by 29AjayKumar 
</script>
Producción: 

6
-55

 

Complejidad de tiempo: O(1), el código se ejecutará en un tiempo constante.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.

Publicación traducida automáticamente

Artículo escrito por ankit15697 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *