El modelo neuronal de McCulloch-Pitts, que fue el modelo ANN más antiguo, tiene solo dos tipos de entradas: excitatoria e inhibidora. Las entradas excitatorias tienen pesos de magnitud positiva y los pesos inhibitorios tienen pesos de magnitud negativa. Las entradas de la neurona de McCulloch-Pitts pueden ser 0 o 1. Tiene una función de umbral como función de activación. Entonces, la señal de salida y out es 1 si la entrada y sum es mayor o igual a un valor de umbral dado, de lo contrario 0. La representación esquemática del modelo es la siguiente:

Modelo McCulloch-Pitts
Las neuronas simples de McCulloch-Pitts se pueden utilizar para diseñar operaciones lógicas. Para ello, los pesos de conexión deben decidirse correctamente junto con la función de umbral (en lugar del valor de umbral de la función de activación). Para un mejor propósito de comprensión, permítanme considerar un ejemplo:
Juan lleva un paraguas si hace sol o si llueve. Hay cuatro situaciones dadas. Necesito decidir cuándo John llevará el paraguas. Las situaciones son las siguientes:
- Primer escenario: No llueve, ni hace sol
- Segundo escenario: No llueve, pero hace sol
- Tercer escenario: está lloviendo y no hace sol
- Cuarto escenario: tanto llueve como hace sol
Para analizar las situaciones utilizando el modelo neuronal de McCulloch-Pitts, puedo considerar las señales de entrada de la siguiente manera:
- X1 : ¿Está lloviendo ?
- X2 : ¿ Hace sol?
Entonces, el valor de ambos escenarios puede ser 0 o 1. Podemos usar el valor de ambos pesos X 1 y X 2 como 1 y una función de umbral como 1. Entonces, el modelo de red neuronal se verá así:

La tabla de verdad para este caso será:
|
Situación |
x1 _ |
x2 _ |
y suma |
fuera _ |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
1 |
1 |
|
3 |
1 |
0 |
1 |
1 |
|
4 |
1 |
1 |
2 |
1 |
Entonces, puedo decir que,
![]()
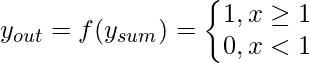
La tabla de verdad construida con respecto al problema se muestra arriba. De la tabla de verdad, puedo concluir que en las situaciones en las que el valor de y out es 1, John necesita llevar un paraguas. Por lo tanto, deberá llevar un paraguas en los escenarios 2, 3 y 4.
El perceptrón de Rosenblatt se basa en el modelo neuronal de McCulloch-Pitts. La representación esquemática es la siguiente:

Perceptrón de Rosenblatt
El perceptrón recibe un conjunto de entradas x 1 , x 2 ,….., x n . El combinador lineal o el modo sumador calcula la combinación lineal de las entradas aplicadas a las sinapsis con pesos sinápticos que son w 1 , w 2 ,……,w n . Luego, el limitador estricto verifica si la suma resultante es positiva o negativa. Si la entrada del Node limitador estricto es positiva, la salida es +1, y si la entrada es negativa, la salida es -1. Matemáticamente, la entrada del limitador duro es:
![]()
Sin embargo, el perceptrón incluye un valor ajustable o sesgo como peso adicional w0 . Este peso adicional se adjunta a una entrada ficticia x 0 , a la que se le asigna un valor de 1. Esta consideración modifica la ecuación anterior a:
![]()
La salida se decide por la expresión:
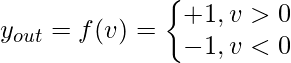
El objetivo del perceptrón es clasificar un conjunto de entradas en dos clases c 1 y c 2 . Esto se puede hacer usando una regla de decisión muy simple: asigne las entradas a c 1 si la salida del perceptrón, es decir, y out es +1 y c 2 si y out es -1. Entonces, para un espacio de señal n-dimensional, es decir, un espacio para ‘n’ señales de entrada, la forma más simple de perceptrón tendrá dos regiones de decisión, que se asemejan a dos clases, separadas por un hiperplano definido por:
![]()
Por lo tanto, las dos señales de entrada indicadas por las variables x 1 y x 2 , el límite de decisión es una línea recta de la forma:
![]() o
o
![]()
Entonces, para un perceptrón que tenga los valores de pesos sinápticos w 0 , w 1 y w 2 como -2, 1/2 y 1/4, respectivamente. El límite de decisión lineal será de la forma:
![]()
![]()
Entonces, cualquier punto (x, 1 x 2 ) que se encuentre por encima del límite de decisión, como se muestra en el gráfico, se asignará a la clase c1 y los puntos que se encuentren por debajo del límite se asignarán a la clase c2.

Por lo tanto, vemos que para un conjunto de datos con clases linealmente separables, los perceptrones siempre se pueden emplear para resolver problemas de clasificación usando líneas de decisión (para espacios bidimensionales), planos de decisión (para espacios tridimensionales) o hiperplanos de decisión (para espacios n-dimensionales). espacio dimensional). Se pueden obtener valores apropiados de los pesos sinápticos entrenando un perceptrón. Sin embargo, una suposición para que el perceptrón funcione correctamente es que las dos clases deben ser linealmente separables, es decir, las clases deben estar suficientemente separadas entre sí. De lo contrario, si las clases no son separables linealmente, el perceptrón no puede resolver el problema de clasificación.

Clases separables lineales frente a no lineales
Perceptrón multicapa: un perceptrón básico funciona muy bien para conjuntos de datos que poseen patrones linealmente separables. Sin embargo, en situaciones prácticas, esa es una situación ideal para tener. Este fue exactamente el punto planteado por Minsky y Papert en su trabajo de 1969. Demostraron que un perceptrón básico no puede aprender a calcular ni siquiera un simple XOR de 2 bits. Entonces, entendamos la razón.
Considere una tabla de verdad que resalta la salida de una función XOR de 2 bits:
|
x1 _ |
x2 _ |
x 1 X O x 2 |
Clase |
|
1 |
1 |
0 |
c 2 |
|
1 |
0 |
1 |
do 1 |
|
0 |
1 |
1 |
do 1 |
|
0 |
0 |
0 |
c 2 |
Los datos no son linealmente separables. Solo un límite de decisión curvo puede separar las clases correctamente. Para solucionar este problema, la otra opción es utilizar dos líneas de límite de decisión en lugar de una.

Clasificación con dos líneas de decisión en la salida de la función XOR
Esta es la filosofía utilizada para diseñar el modelo de perceptrón multicapa. Los aspectos más destacados de este modelo son los siguientes:
- La red neuronal contiene una o más capas intermedias entre los Nodes de entrada y salida, que están ocultas tanto para los Nodes de entrada como para los de salida.
- Cada neurona de la red incluye una función de activación no lineal que es diferenciable.
- Las neuronas de cada capa están conectadas con algunas o todas las neuronas de la capa anterior.
El elemento neural lineal adaptativo (ADALINE) es una RNA de una sola capa temprana desarrollada por el profesor Bernard Widrow de la Universidad de Stanford. Como se muestra en el siguiente diagrama, solo tiene neuronas de salida. El valor de salida puede ser +1 o -1. Se agrega una entrada de polarización x 0 (donde x 0 = 1) que tiene un peso w 0 . La función de activación es tal que si la suma ponderada es positiva o 0, la salida es 1, de lo contrario es -1. Formalmente puedo decir que,
![]()


El algoritmo de aprendizaje supervisado adoptado por la red ADALINE se conoce como Least Mean Square (LMS) o Regla DELTA. Una red que combina varios ADALINE se denomina MADALINE (muchos ADALINE) . Las redes MEADALINE se pueden utilizar para resolver problemas relacionados con la separabilidad no lineal.
Publicación traducida automáticamente
Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA