Longitud de la intersección cortada de una línea por un círculo

Dados seis números enteros, a , b , c , i , j y k que representan la ecuación del círculo $(x^2 + y^2 + ax + by + c = 0)$ y la ecuación de la línea $(ix + jy + k = 0)$ , la tarea es encontrar la longitud de la intersección entre la línea dada y el círculo.

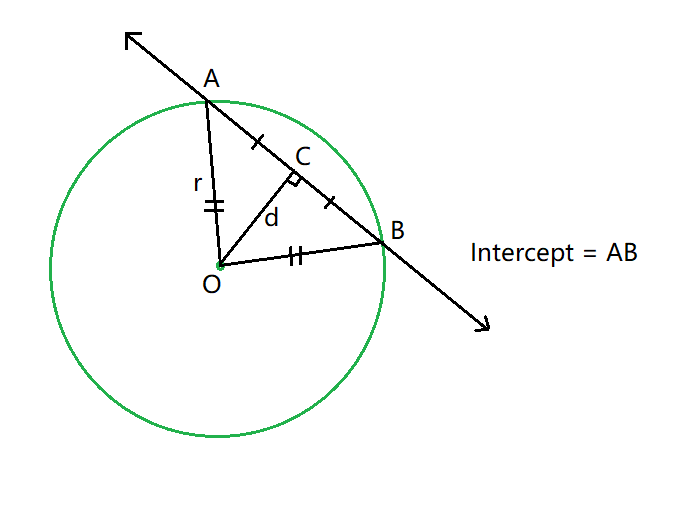
Ejemplos:

Entrada: a = 0, b = 0, c = -4, i = 2, j = -1, k = 1
Salida: 3,89872

Entrada: a = 5, b = 6, c = -16, i = 1, j = 4, k = 3
Salida: 6,9282

Enfoque: siga los pasos a continuación para resolver el problema:

Encuentre el centro del círculo, diga $(x_1, y_1)$ como $x_1 = \frac{a}{2}$ y $y_1 = \frac{b}{2}$ .
La perpendicular desde el centro divide la intersección en dos partes iguales, por lo tanto, calcula la longitud de una de las partes y multiplícala por 2 para obtener la longitud total de la intersección.
Calcula el valor del radio (r) usando la fórmula: $r = \sqrt(g^2 + f^2 - c)$ , donde $g = \frac{a}{2}$ y $f = \frac{b}{2}$
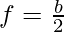
Calcule el valor de la distancia perpendicular ( d ) del centro O desde la línea usando la fórmula: $d = \frac{|ix_1 + jy_1 + k|} {\sqrt{ i^2 + j^2}}$
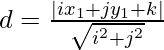
Ahora del teorema de Pitágoras en el triángulo OCA :
- $OC^2 + AC^2 = OA^2$
- $d^2 + AC^2 = r^2$
- $AC^2 = r^2 - d^2$

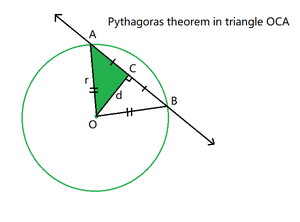
Después de completar los pasos anteriores, imprime el valor del doble de AC para obtener la longitud de la intersección total.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the
// radius of a circle
double radius(int a, int b, int c)
{
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
 
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
 
    // Apply the radius formula
    return (sqrt(g * g + f * f - c));
}
 
// Function to find the perpendicular
// distance between circle center and the line
double centerDistanceFromLine(int a, int b,
                              int i, int j,
                              int k)
{
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
 
    // Stores the perpendicular distance
    // between the line and the point
    double distance
        = fabs(i * g + j * f + k)
          / (sqrt(i * i + j * j));
 
    // Invalid Case
    if (distance < 0)
        return (-1);
 
    // Return the distance
    return distance;
}
 
// Function to find the length of intercept
// cut off from a line by a circle
void interceptLength(int a, int b, int c,
                     int i, int j,
                     int k)
{
    // Calculate the value of radius
    double rad = radius(a, b, c);
 
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(
        a, b, i, j, k);
 
    // Invalid Case
    if (rad < 0 || dist < 0) {
        cout << "circle not possible";
        return;
    }
 
    // If line do not cut circle
    if (dist > rad) {
        cout << "Line not cutting circle";
    }
 
    // Print the intercept length
    else
        cout << 2 * sqrt(
rad * rad - dist * dist);
}
 
// Driver Code
int main()
{
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
 
    // Function Call
    interceptLength(a, b, c, i, j, k);
 
    return 0;
}

Java

// Java program for the above approach
class GFG{
 
// Function to find the
// radius of a circle
static double radius(int a, int b, int c)
{
     
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
 
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
 
    // Apply the radius formula
    return (Math.sqrt(g * g + f * f - c));
}
 
// Function to find the perpendicular
// distance between circle center and the line
static double centerDistanceFromLine(int a, int b,
                                     int i, int j,
                                     int k)
{
     
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
 
    // Stores the perpendicular distance
    // between the line and the point
    double distance = Math.abs(i * g + j * f + k) /
                    (Math.sqrt(i * i + j * j));
 
    // Invalid Case
    if (distance < 0)
        return (-1);
 
    // Return the distance
    return distance;
}
 
// Function to find the length of intercept
// cut off from a line by a circle
static void interceptLength(int a, int b, int c,
                            int i, int j, int k)
{
     
    // Calculate the value of radius
    double rad = radius(a, b, c);
 
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(
        a, b, i, j, k);
 
    // Invalid Case
    if (rad < 0 || dist < 0)
    {
        System.out.println("circle not possible");
        return;
    }
 
    // If line do not cut circle
    if (dist > rad)
    {
        System.out.println("Line not cutting circle");
    }
 
    // Print the intercept length
    else
        System.out.println(2 * Math.sqrt(
            rad * rad - dist * dist));
}
 
// Driver code
public static void main(String[] args)
{
     
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
 
    // Function Call
    interceptLength(a, b, c, i, j, k);
}
}
 
// This code is contributed by abhinavjain194

Python3

# Python3 program for the above approach
import math
 
# Function to find the
# radius of a circle
def radius(a, b, c):
 
    # g and f are the coordinates
    # of the center
    g = a / 2
    f = b / 2
 
    # Case of invalid circle
    if (g * g + f * f - c < 0):
        return(-1)
 
    # Apply the radius formula
    return(math.sqrt(g * g + f * f - c))
 
# Function to find the perpendicular
# distance between circle center and the line
def centerDistanceFromLine(a, b, i, j, k):
 
    # Store the coordinates of center
    g = a / 2
    f = b / 2
 
    # Stores the perpendicular distance
    # between the line and the point
    distance = (abs(i * g + j * f + k) /
         (math.sqrt(i * i + j * j)))
 
    # Invalid Case
    if (distance < 0):
        return (-1)
 
    # Return the distance
    return distance
 
# Function to find the length of intercept
# cut off from a line by a circle
def interceptLength(a, b, c, i, j, k):
 
    # Calculate the value of radius
    rad = radius(a, b, c)
 
    # Calculate the perpendicular distance
    # between line and center
    dist = centerDistanceFromLine(
        a, b, i, j, k)
 
    # Invalid Case
    if (rad < 0 or dist < 0):
        print("circle not possible")
        return
 
    # If line do not cut circle
    if (dist > rad):
        print("Line not cutting circle")
 
    # Print the intercept length
    else:
        print(2 * math.sqrt(
            rad * rad - dist * dist))
 
# Driver Code
if __name__ == "__main__":
 
    # Given Input
    a = 0
    b = 0
    c = -4
    i = 2
    j = -1
    k = 1
 
    # Function Call
    interceptLength(a, b, c, i, j, k)
 
# This code is contributed by ukasp

C#

// C# program for the above approach
using System;
 
class GFG{
     
// Function to find the
// radius of a circle
static double radius(int a, int b, int c)
{
     
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
  
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
  
    // Apply the radius formula
    return(Math.Sqrt(g * g + f * f - c));
}
  
// Function to find the perpendicular
// distance between circle center and the line
static double centerDistanceFromLine(int a, int b,
                                     int i, int j,
                                     int k)
{
     
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
  
    // Stores the perpendicular distance
    // between the line and the point
    double distance = Math.Abs(i * g + j * f + k) /
                    (Math.Sqrt(i * i + j * j));
  
    // Invalid Case
    if (distance < 0)
        return (-1);
  
    // Return the distance
    return distance;
}
  
// Function to find the length of intercept
// cut off from a line by a circle
static void interceptLength(int a, int b, int c,
                            int i, int j, int k)
{
      
    // Calculate the value of radius
    double rad = radius(a, b, c);
  
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(
        a, b, i, j, k);
  
    // Invalid Case
    if (rad < 0 || dist < 0)
    {
        Console.WriteLine("circle not possible");
        return;
    }
  
    // If line do not cut circle
    if (dist > rad)
    {
        Console.WriteLine("Line not cutting circle");
    }
  
    // Print the intercept length
    else
        Console.WriteLine(2 * Math.Sqrt(
            rad * rad - dist * dist));
}
 
// Driver code
public static void Main(String []args)
{
     
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
  
    // Function Call
    interceptLength(a, b, c, i, j, k);
}
}
 
// This code is contributed by sanjoy_62

Javascript

<script>
 
        // JavaScript program for the above approach
 
 
        // Function to find the
        // radius of a circle
        function radius(a, b, c) {
 
            // g and f are the coordinates
            // of the center
            let g = a / 2;
            let f = b / 2;
 
            // Case of invalid circle
            if (g * g + f * f - c < 0)
                return (-1);
 
            // Apply the radius formula
            return (Math.sqrt(g * g + f * f - c));
        }
 
        // Function to find the perpendicular
        // distance between circle center and the line
        function centerDistanceFromLine(a, b, i, j, k) {
 
            // Store the coordinates of center
            let g = a / 2;
            let f = b / 2;
 
            // Stores the perpendicular distance
            // between the line and the point
            let distance = Math.abs(i * g + j * f + k) /
                (Math.sqrt(i * i + j * j));
 
            // Invalid Case
            if (distance < 0)
                return (-1);
 
            // Return the distance
            return distance;
        }
 
        // Function to find the length of intercept
        // cut off from a line by a circle
        function interceptLength(a, b, c, i, j, k) {
 
            // Calculate the value of radius
            let rad = radius(a, b, c);
 
            // Calculate the perpendicular distance
            // between line and center
            let dist = centerDistanceFromLine(
                a, b, i, j, k);
 
            // Invalid Case
            if (rad < 0 || dist < 0) {
                document.write("circle not possible");
                return;
            }
 
            // If line do not cut circle
            if (dist > rad) {
                document.write("Line not cutting circle");
            }
 
            // Print the intercept length
            else
                document.write(2 * Math.sqrt(
                    rad * rad - dist * dist));
        }
 
        // Driver code
 
        // Given Input
        let a = 0, b = 0, c = -4;
        let i = 2, j = -1, k = 1;
 
        // Function Call
        interceptLength(a, b, c, i, j, k);
 
        // This code is contributed by Hritik
         
</script>

Producción:

3.89872

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por arjundevmishra6 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta