Un proceso de Renovación es un caso general de Proceso de Poisson en el que el tiempo entre llegadas del proceso o el tiempo entre fallas no sigue necesariamente la distribución exponencial. Un proceso de conteo N(t) que representa el número total de ocurrencias de un evento en el intervalo de tiempo (0, t] se denomina proceso de renovación, si el tiempo entre fallas son variables aleatorias independientes e idénticamente distribuidas.
La probabilidad de que ocurran exactamente n fallas en el tiempo t se puede escribir como, ![]()
y,![]()
Tenga en cuenta que los tiempos entre las fallas son T1, T2, …, Tn, por lo que las fallas que ocurren en el tiempo ![]() son,
son, ![]()
por lo tanto,![]()
![]()
![]()
![]()
Propiedades –
- La función de valor medio del proceso de renovación, denotada por m(t), es igual a la suma de la función de distribución de todos los tiempos de renovación, es decir,
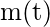
![Rendered by QuickLaTeX.com $= E[N(t)] $](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b399315e6a347da09d4ac9e9fd1c4ea2_l3.png)
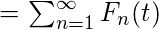
- La función de renovación, m(t), satisface la siguiente ecuación:
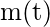
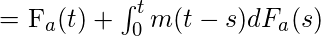
donde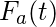 es la función de distribución del tiempo entre llegadas o el período de renovación.
es la función de distribución del tiempo entre llegadas o el período de renovación.