Dada una array arr[] y un entero K , la tarea es encontrar la máxima suma de K elementos en la array tomando solo los elementos de las esquinas.
Un elemento de esquina es un elemento desde el principio de la array o desde el final de la array.
Ejemplos:
Entrada: arr[] = {8, 4, 4, 8, 12, 3, 2, 9}, K = 3
Salida: 21
Explicación:
la estrategia óptima es elegir los elementos de la array, dos índices desde el principio y un índice desde el final. Todas las demás opciones posibles producirán una suma menor. Por lo tanto, arr[0] + arr[1] + arr[7] = 21.Entrada: arr[] = {2, 1, 14, 6, 4, 3}, K = 3
Salida: 17
Explicación:
Obtendremos la suma máxima seleccionando los primeros tres elementos de la array. Por lo tanto, la elección óptima es: arr[0] + arr[1] + arr[2] = 17
Enfoque Naive: La idea es usar Recursion . Como solo podemos tomar un valor de índice inicial o final, inicialice dos variables y tome exactamente K pasos y devuelva la suma máxima entre todas las combinaciones posibles. El enfoque recursivo tiene una complejidad exponencial debido a su subproblema superpuesto y su propiedad de subestructura óptima .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to maximize the sum of K elements
// in the array by taking only corner elements
#include <bits/stdc++.h>
using namespace std;
// Function to return maximum sum
int maxSum(int arr[], int K, int start, int end, int max_sum)
{
// Base case
if (K == 0)
return max_sum;
// Pick the start index
int max_sum_start = max_sum + arr[start];
// Pick the end index
int max_sum_end = max_sum + arr[end];
// Recursive function call
int ans = max(
maxSum(arr, K - 1, start + 1, end, max_sum_start),
maxSum(arr, K - 1, start, end - 1, max_sum_end));
// Return the final answer
return ans;
}
// Function to find the maximized sum
void maximizeSum(int arr[], int K, int n)
{
int max_sum = 0;
int start = 0;
int end = n - 1;
cout << maxSum(arr, K, start, end, max_sum);
}
// Driver code
int main()
{
int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = sizeof(arr) / sizeof(arr[0]);
maximizeSum(arr, K, n);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C++ program to maximize the sum of K elements
// in the array by taking only corner elements
#include <stdio.h>
// Find maximum between two numbers.
int max(int num1, int num2)
{
return (num1 > num2 ) ? num1 : num2;
}
// Function to return maximum sum
int maxSum(int arr[], int K, int start, int end, int max_sum)
{
// Base case
if (K == 0)
return max_sum;
// Pick the start index
int max_sum_start = max_sum + arr[start];
// Pick the end index
int max_sum_end = max_sum + arr[end];
// Recursive function call
int ans = max(
maxSum(arr, K - 1, start + 1, end, max_sum_start),
maxSum(arr, K - 1, start, end - 1, max_sum_end));
// Return the final answer
return ans;
}
// Function to find the maximized sum
void maximizeSum(int arr[], int K, int n)
{
int max_sum = 0;
int start = 0;
int end = n - 1;
printf("%d",maxSum(arr, K, start, end, max_sum));
}
// Driver code
int main()
{
int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = sizeof(arr) / sizeof(arr[0]);
maximizeSum(arr, K, n);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java program to maximize the sum of K elements
// in the array by taking only corner elements
import java.util.*;
class GFG {
// Function to return maximum sum
static int maxSum(int arr[], int K, int start, int end, int max_sum)
{
// Base case
if (K == 0)
return max_sum;
// Pick the start index
int max_sum_start = max_sum + arr[start];
// Pick the end index
int max_sum_end = max_sum + arr[end];
// Recursive function call
int ans = Math.max(maxSum(arr, K - 1, start + 1, end, max_sum_start),
maxSum(arr, K - 1, start, end - 1, max_sum_end));
// Return the final answer
return ans;
}
// Function to find the maximized sum
static void maximizeSum(int arr[], int K, int n)
{
int max_sum = 0;
int start = 0;
int end = n - 1;
System.out.print(maxSum(arr, K, start, end, max_sum));
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = arr.length;
maximizeSum(arr, K, n);
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# Python3 program to maximize the sum of K elements # in the array by taking only corner elements # Function to return maximum sum def maxSum(arr, K, start, end, max_sum): # Base case if (K == 0): return max_sum # Pick the start index max_sum_start = max_sum + arr[start] # Pick the end index max_sum_end = max_sum + arr[end] # Recursive function call ans = max(maxSum(arr, K - 1, start + 1, end, max_sum_start), maxSum(arr, K - 1, start, end - 1, max_sum_end)) # Return the final answer return ans # Function to find the maximized sum def maximizeSum(arr, K, n): max_sum = 0 start = 0 end = n - 1 print(maxSum(arr, K, start, end, max_sum)) # Driver code if __name__ == '__main__': arr = [8, 4, 4, 8, 12, 3, 2, 9] K = 3 n = len(arr) maximizeSum(arr, K, n) # This code is contributed by Bhupendra_Singh
C#
// C# program to maximize the sum of K elements
// in the array by taking only corner elements
using System;
class GFG{
// Function to return maximum sum
static int maxSum(int []arr, int K,
int start, int end,
int max_sum)
{
// Base case
if (K == 0)
return max_sum;
// Pick the start index
int max_sum_start = max_sum + arr[start];
// Pick the end index
int max_sum_end = max_sum + arr[end];
// Recursive function call
int ans = Math.Max(maxSum(arr, K - 1, start + 1,
end, max_sum_start),
maxSum(arr, K - 1, start,
end - 1, max_sum_end));
// Return the readonly answer
return ans;
}
// Function to find the maximized sum
static void maximizeSum(int []arr, int K, int n)
{
int max_sum = 0;
int start = 0;
int end = n - 1;
Console.Write(maxSum(arr, K, start,
end, max_sum));
}
// Driver code
public static void Main(String[] args)
{
int []arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = arr.Length;
maximizeSum(arr, K, n);
}
}
// This code is contributed by sapnasingh4991
Javascript
<script>
// Javascript program to maximize the sum of K elements
// in the array by taking only corner elements
// Function to return maximum sum
function maxSum(arr, K,
start, end,
max_sum)
{
// Base case
if (K == 0)
return max_sum;
// Pick the start index
let max_sum_start = max_sum + arr[start];
// Pick the end index
let max_sum_end = max_sum + arr[end];
// Recursive function call
let ans = Math.max(maxSum(arr, K - 1, start + 1,
end, max_sum_start),
maxSum(arr, K - 1, start,
end - 1, max_sum_end));
// Return the final answer
return ans;
}
// Function to find the maximized sum
function maximizeSum(arr, K, n)
{
let max_sum = 0;
let start = 0;
let end = n - 1;
document.write(maxSum(arr, K, start,
end, max_sum));
}
// Driver Code
let arr = [ 8, 4, 4, 8, 12, 3, 2, 9 ];
let K = 3;
let n = arr.length;
maximizeSum(arr, K, n);
</script>
21
Complejidad de tiempo: O(2^N)
Espacio Auxiliar: O(N)
Enfoque eficiente: para resolver el problema de manera más eficiente, implementaremos el concepto de ventana deslizante .
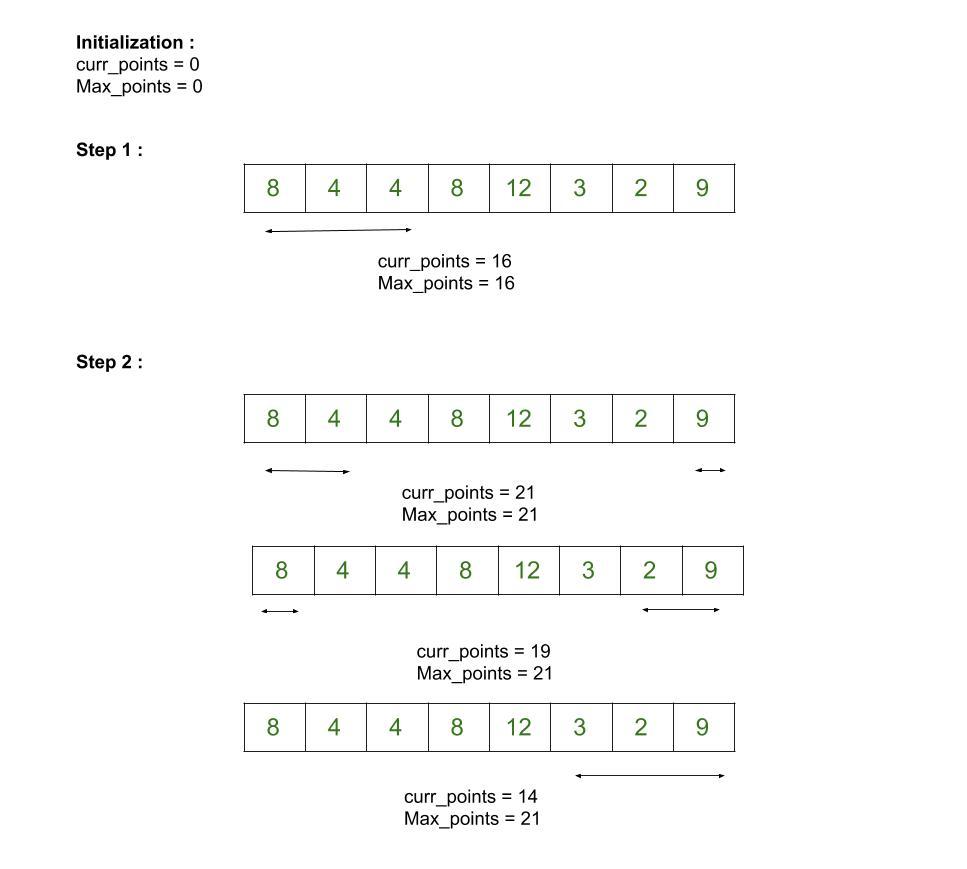
- Inicialice dos enteros con 0, curr_points y max_points para representar puntos actuales y puntos máximos respectivamente.
- Ahora, itere sobre K elementos uno por uno desde el principio y forme la ventana de tamaño K, también actualice el valor de curr_points con curr_points + arr[i] y max_points con el valor de curr_points .
- Después de eso, en cada paso, tome un elemento del final de la array y elimine el elemento más a la derecha de la ventana previamente seleccionada con elementos iniciales donde el tamaño de la ventana siempre permanece K. Actualice los valores para curr_points y max_points en consecuencia . Por fin, tenemos K elementos del final de la array y max_points contiene el resultado requerido que debe devolverse.
Veamos la siguiente imagen para entenderlo mejor:
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to maximize the sum of K elements
// in the array by taking only corner elements
#include <bits/stdc++.h>
using namespace std;
// Function to return maximum sum
int maxPointCount(int arr[], int K, int size)
{
// Initialize variables
int curr_points = 0;
int max_points = 0;
// Iterate over first K elements of array and update the
// value for curr_points
for (int i = 0; i < K; i++)
curr_points += arr[i];
// Update value for max_points
max_points = curr_points;
// j points to the end of the array
int j = size - 1;
for (int i = K - 1; i >= 0; i--) {
curr_points = curr_points + arr[j] - arr[i];
max_points = max(curr_points, max_points);
j--;
}
// Return the final result
return max_points;
}
// Driver code
int main()
{
int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = sizeof(arr) / sizeof(arr[0]);
cout << maxPointCount(arr, K, n);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C program to maximize the sum of K elements
// in the array by taking only corner elements
#include <stdio.h>
// Find maximum between two numbers.
int max(int num1, int num2)
{
return (num1 > num2 ) ? num1 : num2;
}
// Function to return maximum sum
int maxPointCount(int arr[], int K, int size)
{
// Initialize variables
int curr_points = 0;
int max_points = 0;
// Iterate over first K elements of array and update the
// value for curr_points
for (int i = 0; i < K; i++)
curr_points += arr[i];
// Update value for max_points
max_points = curr_points;
// j points to the end of the array
int j = size - 1;
for (int i = K - 1; i >= 0; i--) {
curr_points = curr_points + arr[j] - arr[i];
max_points = max(curr_points, max_points);
j--;
}
// Return the final result
return max_points;
}
// Driver code
int main()
{
int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = sizeof(arr) / sizeof(arr[0]);
printf("%d",maxPointCount(arr, K, n));
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java program to maximize the sum of K elements in the
// array by taking only corner elements
import java.util.Arrays;
import java.util.Scanner;
class GFG {
// Function to return maximum sum
public static int maxPointCount(int arr[], int K, int size)
{
// Initialize variables
int curr_points = 0;
int max_points = 0;
// Iterate over first K elements of array and update
// the value for curr_points
for (int i = 0; i < K; i++)
curr_points += arr[i];
// Update value for max_points
max_points = curr_points;
// j points to the end of the array
int j = size - 1;
for (int i = K - 1; i >= 0; i--) {
curr_points = curr_points + arr[j] - arr[i];
max_points = Math.max(curr_points, max_points);
j--;
}
// Return the final result
return max_points;
}
// Driver code
public static void main(String args[])
{
int[] arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = arr.length;
System.out.print(maxPointCount(arr, K, n));
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# Python3 program to maximize the sum # of K elements in the array by taking # only corner elements # Function to return maximum sum def maxPointCount(arr, K, size): # Initialize variables curr_points = 0 max_points = 0 # Iterate over first K elements # of array and update the value # for curr_points for i in range(K): curr_points += arr[i] # Update value for max_points max_points = curr_points # j points to the end of the array j = size - 1 for i in range(K - 1, -1, -1): curr_points = (curr_points + arr[j] - arr[i]) max_points = max(curr_points, max_points) j -= 1 # Return the final result return max_points # Driver code if __name__ == "__main__": arr = [ 8, 4, 4, 8, 12, 3, 2, 9 ] K = 3 n = len(arr) print(maxPointCount(arr, K, n)) # This code is contributed by chitranayal
C#
// C# program to maximize the sum
// of K elements in the array by
// taking only corner elements
using System;
class GFG{
// Function to return maximum sum
public static int maxPointCount(int []arr,
int K,
int size)
{
// Initialize variables
int curr_points = 0;
int max_points = 0;
// Iterate over first K elements
// of array and update the value
// for curr_points
for(int i = 0; i < K; i++)
curr_points += arr[i];
// Update value for max_points
max_points = curr_points;
// j points to the end of the array
int j = size - 1;
for(int i = K - 1; i >= 0; i--)
{
curr_points = curr_points +
arr[j] - arr[i];
max_points = Math.Max(curr_points,
max_points);
j--;
}
// Return the readonly result
return max_points;
}
// Driver code
public static void Main(String []args)
{
int []arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
int K = 3;
int n = arr.Length;
Console.Write( maxPointCount(arr, K, n));
}
}
// This code is contributed by sapnasingh4991
Javascript
<script>
// JavaScript program to maximize the sum
// of K elements in the array by
// taking only corner elements
// Function to return maximum sum
function maxPointCount(arr,k,size)
{
// Initialize variables
let curr_points = 0;
let max_points = 0;
// Iterate over first K elements
// of array and update the value
// for curr_points
for(let i = 0; i < K; i++)
curr_points += arr[i];
// Update value for max_points
max_points = curr_points;
// j points to the end of the array
let j = size - 1;
for(let i = K - 1; i >= 0; i--)
{
curr_points = curr_points +
arr[j] - arr[i];
max_points = Math.max(curr_points,
max_points);
j--;
}
// Return the final result
return max_points;
}
// Driver code
let arr=[8, 4, 4, 8, 12, 3, 2, 9];
let K = 3;
let n = arr.length;
document.write( maxPointCount(arr, K, n));
// This code is contributed by avanitrachhadiya2155
</script>
21
Complejidad de tiempo: O(N) , donde N es el tamaño de la array.
Complejidad del espacio auxiliar: O(1) .
Publicación traducida automáticamente
Artículo escrito por animesh_ghosh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA