Dados N bloques, de los cuales K está coloreado. Estos bloques de color K se indican mediante una array arr[] . La tarea consiste en contar el número de formas de colorear los bloques restantes sin colorear, de modo que solo cualquiera de los bloques adyacentes, de un bloque coloreado, pueda colorearse en un solo paso. Imprime la respuesta con módulo 10 9 +7.
Ejemplos:
Entrada: N = 6, K = 3, arr[] = {1, 2, 6}
Salida: 4
Explicación:
Las siguientes son las 4 formas de colorear los bloques (cada conjunto reblockquotesenvía el orden en que se colorean los bloques):
1 {3, 4, 5}
2. {3, 5, 4}
3. {5, 3, 4}
4. {5, 4, 3}Entrada: N = 9, K = 3, A = [3, 6, 7]
Salida: 180
Enfoque ingenuo: la idea es utilizar la recursividad . A continuación se muestran los pasos:
- Atraviesa cada bloque de 1 a N.
- Si el bloque actual (por ejemplo, b ) no está coloreado, compruebe si uno de los bloques adyacentes está coloreado o no.
- Si el bloque adyacente está coloreado, coloree el bloque actual e itere recursivamente para encontrar el siguiente bloque sin color.
- Después de que finalice la llamada recursiva anterior, elimine el color del bloque para la llamada recursiva anterior de blockquote y repita los pasos anteriores para el siguiente bloque sin color.
- El recuento de colorear los bloques en todas las llamadas recursivas anteriores da la cantidad de formas de colorear el bloque sin colorear.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
// Recursive function to count the ways
int countWays(int colored[], int count,
int n)
{
// Base case
if (count == n) {
return 1;
}
// Initialise answer to 0
int answer = 0;
// Color each uncolored block according
// to the given condition
for (int i = 1; i < n + 1; i++) {
// If any block is uncolored
if (colored[i] == 0) {
// Check if adjacent blocks
// are colored or not
if (colored[i - 1] == 1
|| colored[i + 1] == 1) {
// Color the block
colored[i] = 1;
// recursively iterate for
// next uncolored block
answer = (answer
+ countWays(colored,
count + 1,
n))
% mod;
// Uncolored for the next
// recursive call
colored[i] = 0;
}
}
}
// Return the final count
return answer;
}
// Function to count the ways to color
// block
int waysToColor(int arr[], int n, int k)
{
// Mark which blocks are colored in
// each recursive step
int colored[n + 2] = { 0 };
for (int i = 0; i < k; i++) {
colored[arr[i]] = 1;
}
// Function call to count the ways
return countWays(colored, k, n);
}
// Driver Code
int main()
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int arr[K] = { 1, 2, 6 };
// Function call
cout << waysToColor(arr, N, K);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
class GFG{
static int mod = 1000000007;
// Recursive function to count the ways
static int countWays(int colored[],
int count, int n)
{
// Base case
if (count == n)
{
return 1;
}
// Initialise answer to 0
int answer = 0;
// Color each uncolored block according
// to the given condition
for (int i = 1; i < n + 1; i++)
{
// If any block is uncolored
if (colored[i] == 0)
{
// Check if adjacent blocks
// are colored or not
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
// Color the block
colored[i] = 1;
// recursively iterate for
// next uncolored block
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
// Uncolored for the next
// recursive call
colored[i] = 0;
}
}
}
// Return the final count
return answer;
}
// Function to count the ways to color
// block
static int waysToColor(int arr[],
int n, int k)
{
// Mark which blocks are colored in
// each recursive step
int colored[] = new int[n + 2];
for (int i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
// Function call to count the ways
return countWays(colored, k, n);
}
// Driver Code
public static void main(String[] args)
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int arr[] = { 1, 2, 6 };
// Function call
System.out.print(waysToColor(arr, N, K));
}
}
// This code is contributed by sapnasingh4991
Python3
# Python3 program for the above approach mod = 1000000007 # Recursive function to count the ways def countWays(colored, count, n): # Base case if (count == n): return 1 # Initialise answer to 0 answer = 0 # Color each uncolored block according # to the given condition for i in range(1, n + 1): # If any block is uncolored if (colored[i] == 0): # Check if adjacent blocks # are colored or not if (colored[i - 1] == 1 or colored[i + 1] == 1): # Color the block colored[i] = 1 # recursively iterate for # next uncolored block answer = ((answer + countWays(colored, count + 1, n)) % mod) # Uncolored for the next # recursive call colored[i] = 0 # Return the final count return answer # Function to count the ways to color # block def waysToColor( arr, n, k): # Mark which blocks are colored in # each recursive step colored = [0] * (n + 2) for i in range(k): colored[arr[i]] = 1 # Function call to count the ways return countWays(colored, k, n) # Driver Code if __name__ == "__main__": # Number of blocks N = 6 # Number of colored blocks K = 3 arr = [ 1, 2, 6 ] # Function call print(waysToColor(arr, N, K)) # This code is contributed by chitranayal
C#
// C# program for the above approach
using System;
class GFG{
static int mod = 1000000007;
// Recursive function to count the ways
static int countWays(int []colored,
int count, int n)
{
// Base case
if (count == n)
{
return 1;
}
// Initialise answer to 0
int answer = 0;
// Color each uncolored block according
// to the given condition
for (int i = 1; i < n + 1; i++)
{
// If any block is uncolored
if (colored[i] == 0)
{
// Check if adjacent blocks
// are colored or not
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
// Color the block
colored[i] = 1;
// recursively iterate for
// next uncolored block
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
// Uncolored for the next
// recursive call
colored[i] = 0;
}
}
}
// Return the final count
return answer;
}
// Function to count the ways to color
// block
static int waysToColor(int []arr,
int n, int k)
{
// Mark which blocks are colored in
// each recursive step
int []colored = new int[n + 2];
for (int i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
// Function call to count the ways
return countWays(colored, k, n);
}
// Driver Code
public static void Main()
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int []arr = { 1, 2, 6 };
// Function call
Console.Write(waysToColor(arr, N, K));
}
}
// This code is contributed by Code_Mech
Javascript
<script>
// Javascript program for the above approach
let mod = 1000000007;
// Recursive function to count the ways
function countWays(colored,
count, n)
{
// Base case
if (count == n)
{
return 1;
}
// Let initialise answer to 0
let answer = 0;
// Color each uncolored block according
// to the given condition
for (let i = 1; i < n + 1; i++)
{
// If any block is uncolored
if (colored[i] == 0)
{
// Check if adjacent blocks
// are colored or not
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
// Color the block
colored[i] = 1;
// recursively iterate for
// next uncolored block
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
// Uncolored for the next
// recursive call
colored[i] = 0;
}
}
}
// Return the final count
return answer;
}
// Function to count the ways to color
// block
function waysToColor(arr, n, k)
{
// Mark which blocks are colored in
// each recursive step
let colored = Array.from({length: n+2}, (_, i) => 0);
for (let i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
// Function call to count the ways
return countWays(colored, k, n);
}
// Driver Code
// Number of blocks
let N = 6;
// Number of colored blocks
let K = 3;
let arr = [ 1, 2, 6 ];
// Function call
document.write(waysToColor(arr, N, K));
</script>
4
Complejidad de tiempo: O(N N-K )
Espacio Auxiliar: O(N)
Enfoque Eficiente: Para resolver este problema de manera eficiente utilizaremos el concepto de Permutación y Combinación . A continuación se muestran los pasos:
1. Si el número de bloques entre dos bloques de colores consecutivos es x, entonces el número de formas de colorear este conjunto de bloques viene dado por:
caminos = 2 x-1
2. Colorear cada conjunto de bloques sin colorear es independiente del otro. Supongamos que hay x bloques en una sección e y bloques en la otra sección. Para encontrar la combinación total cuando las dos secciones se fusionan viene dada por:
combinaciones totales =
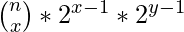
3. Ordene los índices de bloques coloreados para encontrar la longitud de cada sección de bloque sin color e itere y encuentre la combinación de cada dos secciones usando la fórmula anterior.
4. Encuentre el coeficiente binomial utilizando el enfoque que se analiza en este artículo.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
// Function to count the ways to color
// block
int waysToColor(int arr[], int n, int k)
{
// For storing powers of 2
int powOf2[500] = { 0 };
// For storing binomial coefficient
// values
int c[500][500];
// Calculating binomial coefficient
// using DP
for (int i = 0; i <= n; i++) {
c[i][0] = 1;
for (int j = 1; j <= i; j++) {
c[i][j] = (c[i - 1][j]
+ c[i - 1][j - 1])
% mod;
}
}
powOf2[0] = powOf2[1] = 1;
// Calculating powers of 2
for (int i = 2; i <= n; i++) {
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
// Sort the indices to calculate
// length of each section
sort(arr, arr + k);
// Initialise answer to 1
int answer = 1;
for (int i = 0; i < k; i++) {
// Find the length of each section
int x = arr[i] - (i - 1 >= 0
? arr[i - 1]
: 0)
- 1;
// Merge this section
answer *= c[rem][x] % mod * (i != 0
&& i != k - 1
? powOf2[x]
: 1)
% mod;
rem -= x;
}
// Return the final count
return answer;
}
// Driver Code
int main()
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int arr[K] = { 1, 2, 6 };
// Function call
cout << waysToColor(arr, N, K);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
class GFG{
static int mod = 1000000007;
// Function to count the ways to color
// block
static int waysToColor(int arr[], int n, int k)
{
// For storing powers of 2
int powOf2[] = new int[500];
// For storing binomial coefficient
// values
int [][]c = new int[500][500];
// Calculating binomial coefficient
// using DP
for(int i = 0; i <= n; i++)
{
c[i][0] = 1;
for(int j = 1; j <= i; j++)
{
c[i][j] = (c[i - 1][j] +
c[i - 1][j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
// Calculating powers of 2
for(int i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
// Sort the indices to calculate
// length of each section
Arrays.sort(arr);
// Initialise answer to 1
int answer = 1;
for(int i = 0; i < k; i++)
{
// Find the length of each section
int x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
// Merge this section
answer *= c[rem][x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
// Return the final count
return answer;
}
// Driver Code
public static void main(String[] args)
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int arr[] = { 1, 2, 6 ,0 };
// Function call
System.out.print(waysToColor(arr, N, K));
}
}
// This code is contributed by 29AjayKumar
Python3
# Python3 program for the above approach mod = 1000000007 # Function to count the ways to color # block def waysToColor(arr, n, k): global mod # For storing powers of 2 powOf2 = [0 for i in range(500)] # For storing binomial coefficient # values c = [[0 for i in range(500)] for j in range(500)] # Calculating binomial coefficient # using DP for i in range(n + 1): c[i][0] = 1; for j in range(1, i + 1): c[i][j] = (c[i - 1][j]+ c[i - 1][j - 1])% mod; powOf2[0] = 1 powOf2[1] = 1; # Calculating powers of 2 for i in range(2, n + 1): powOf2[i] = (powOf2[i - 1] * 2) % mod; rem = n - k; arr[k] = n + 1; k += 1 # Sort the indices to calculate # length of each section arr.sort() # Initialise answer to 1 answer = 1; for i in range(k): x = 0 # Find the length of each section if i - 1 >= 0: x = arr[i] - arr[i - 1] -1 else: x = arr[i] - 1 # Merge this section answer = answer * (c[rem][x] % mod) * ((powOf2[x] if (i != 0 and i != k - 1) else 1))% mod rem -= x; # Return the final count return answer; # Driver Code if __name__=='__main__': # Number of blocks N = 6; # Number of colored blocks K = 3; arr = [ 1, 2, 6, 0] # Function call print(waysToColor(arr, N, K)) # This code is contributed by rutvik_56
C#
// C# program for the above approach
using System;
class GFG{
static int mod = 1000000007;
// Function to count the ways to color
// block
static int waysToColor(int []arr, int n, int k)
{
// For storing powers of 2
int []powOf2 = new int[500];
// For storing binomial coefficient
// values
int [,]c = new int[500, 500];
// Calculating binomial coefficient
// using DP
for(int i = 0; i <= n; i++)
{
c[i, 0] = 1;
for(int j = 1; j <= i; j++)
{
c[i, j] = (c[i - 1, j] +
c[i - 1, j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
// Calculating powers of 2
for(int i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
// Sort the indices to calculate
// length of each section
Array.Sort(arr);
// Initialise answer to 1
int answer = 1;
for(int i = 0; i < k; i++)
{
// Find the length of each section
int x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
// Merge this section
answer *= c[rem, x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
// Return the readonly count
return answer;
}
// Driver Code
public static void Main(String[] args)
{
// Number of blocks
int N = 6;
// Number of colored blocks
int K = 3;
int []arr = { 1, 2, 6, 0 };
// Function call
Console.Write(waysToColor(arr, N, K));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript program for the above approach
let mod = 1000000007;
// Function to count the ways to color
// block
function waysToColor(arr,n,k)
{
// For storing powers of 2
let powOf2 = new Array(500);
// For storing binomial coefficient
// values
let c = new Array(500);
for(let i=0;i<500;i++)
{
c[i]=new Array(500);
for(let j=0;j<500;j++)
{
c[i][j]=0;
}
}
// Calculating binomial coefficient
// using DP
for(let i = 0; i <= n; i++)
{
c[i][0] = 1;
for(let j = 1; j <= i; j++)
{
c[i][j] = (c[i - 1][j] +
c[i - 1][j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
// Calculating powers of 2
for(let i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
let rem = n - k;
arr[k++] = n + 1;
// Sort the indices to calculate
// length of each section
arr.sort(function(a,b){return a-b;});
// Initialise answer to 1
let answer = 1;
for(let i = 0; i < k; i++)
{
// Find the length of each section
let x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
// Merge this section
answer *= c[rem][x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
// Return the final count
return answer;
}
// Driver Code
// Number of blocks
let N = 6;
// Number of colored blocks
let K = 3;
let arr=[ 1, 2, 6 ,0];
// Function call
document.write(waysToColor(arr, N, K));
// This code is contributed by avanitrachhadiya2155
</script>
4
Complejidad temporal: O(N 2 )
Espacio auxiliar: O(5 2 * 10 4 )