Número de triángulos posibles en un sistema de coordenadas cartesianas

Dados n puntos en un sistema de coordenadas cartesianas. Cuenta el número de triángulos formados. 

Ejemplos: 

Input  : point[] = {(0, 0), (1, 1), (2, 0), (2, 2)
Output : 3
Three triangles can be formed from above points.

Una solución sencilla es comprobar si el determinante de los tres puntos seleccionados es distinto de cero o no. El siguiente determinante da el área de un Triángulo (también conocida como regla de Cramer).
El área del triángulo con esquinas en (x1, y1), (x2, y2) y (x3, y3) está dada por: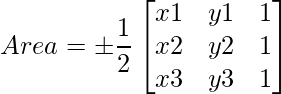

Podemos resolver esto tomando todas las combinaciones posibles de 3 puntos y encontrando el determinante.

// C++ program to count number of triangles that can
// be formed with given points in 2D
#include <bits/stdc++.h>
using namespace std;
 
// A point in 2D
struct Point
{
   int x, y;
};
 
// Returns determinant value of three points in 2D
int det(int x1, int y1, int x2, int y2, int x3, int y3)
{
   return x1*(y2 - y3) - y1*(x2 - x3) + 1*(x2*y3 - y2*x3);
}
 
// Returns count of possible triangles with given array
// of points in 2D.
int countPoints(Point arr[], int n)
{
    int result = 0;  // Initialize result
 
    // Consider all triplets of points given in inputs
    // Increment the result when determinant of a triplet
    // is not 0.
    for (int i=0; i<n; i++)
        for (int j=i+1; j<n; j++)
            for (int k=j+1; k<n; k++)
                if (det(arr[i].x, arr[i].y, arr[j].x,
                        arr[j].y, arr[k].x, arr[k].y))
                    result++;
 
    return result;
}
 
// Driver code
int main()
{
    Point arr[] = {{0, 0}, {1, 1}, {2, 0}, {2, 2}};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << countPoints(arr, n);
    return 0;
}

// Java program to count number
// of triangles that can be formed
// with given points in 2D
 
class GFG{
// Returns determinant value
// of three points in 2D
static int det(int x1, int y1, int x2, int y2, int x3, int y3)
{
    return (x1 * (y2 - y3) - y1 *
        (x2 - x3) + 1 * (x2 *
            y3 - y2 * x3));
}
 
// Returns count of possible
// triangles with given array
// of points in 2D.
static int countPoints(int [][]Point, int n)
{
    int result = 0; // Initialize result
 
    // Consider all triplets of
    // points given in inputs
    // Increment the result when
    // determinant of a triplet is not 0.
    for(int i = 0; i < n; i++)
        for(int j = i + 1; j < n; j++)
            for(int k = j + 1; k < n; k++)
                if(det(Point[i][0], Point[i][1],
                    Point[j][0], Point[j][1],
                    Point[k][0], Point[k][1])>=0)
                    result = result + 1;
 
    return result;
}
 
// Driver code
public static void main(String[] args)
{
int Point[][] = {{0, 0},{1, 1},{2, 0},{2, 2}};
int n = Point.length;
System.out.println(countPoints(Point, n));
}
}
// This code is contributed by
// mits

# Python program to count number
# of triangles that can be formed
# with given points in 2D
 
# Returns determinant value
# of three points in 2D
def det(x1, y1, x2, y2, x3, y3):
    return (x1 * (y2 - y3) - y1 *
            (x2 - x3) + 1 * (x2 *
             y3 - y2 * x3))
 
# Returns count of possible
# triangles with given array
# of points in 2D.
def countPoints(Point, n):
 
    result = 0 # Initialize result
 
    # Consider all triplets of
    # points given in inputs
    # Increment the result when
    # determinant of a triplet is not 0.
    for i in range(n):
        for j in range(i + 1, n):
            for k in range(j + 1, n):
                if(det(Point[i][0], Point[i][1],
                       Point[j][0], Point[j][1],
                       Point[k][0], Point[k][1])):
                    result = result + 1
 
    return result
 
# Driver code
Point = [[0, 0], [1, 1],
         [2, 0], [2, 2]]
n = len(Point)
print(countPoints(Point, n))
 
# This code is contributed by
# Sanjit_Prasad

// C# program to count number
// of triangles that can be formed
// with given points in 2D
using System;
 
class GFG{
// Returns determinant value
// of three points in 2D
static int det(int x1, int y1, int x2, int y2, int x3, int y3)
{
    return (x1 * (y2 - y3) - y1 *
        (x2 - x3) + 1 * (x2 *
            y3 - y2 * x3));
}
 
// Returns count of possible
// triangles with given array
// of points in 2D.
static int countPoints(int[,] Point, int n)
{
    int result = 0; // Initialize result
 
    // Consider all triplets of
    // points given in inputs
    // Increment the result when
    // determinant of a triplet is not 0.
    for(int i = 0; i < n; i++)
        for(int j = i + 1; j < n; j++)
            for(int k = j + 1; k < n; k++)
                if(det(Point[i,0], Point[i,1], Point[j,0], Point[j,1],Point[k,0], Point[k,1])>=0)
                    result = result + 1;
 
    return result;
}
 
// Driver code
public static void Main()
{
int[,] Point = new int[,] { { 0, 0 }, { 1, 1 }, { 2, 0 }, { 2, 2 } };
int n = Point.Length/Point.Rank;
Console.WriteLine(countPoints(Point, n));
}
}
// This code is contributed by mits

<?php
// PHP program to count number
// of triangles that can be formed
// with given points in 2D
 
// Returns determinant value
// of three points in 2D
function det($x1, $y1, $x2,
             $y2, $x3, $y3)
{
    return ($x1 * ($y2 - $y3) - $y1 *
           ($x2 - $x3) + 1 * ($x2 *
            $y3 - $y2 * $x3));
}
 
// Returns count of possible
// triangles with given array
// of points in 2D.
function countPoints($Point, $n)
{
    $result = 0; // Initialize result
 
    // Consider all triplets of
    // points given in inputs
    // Increment the result when
    // determinant of a triplet is not 0.
    for($i = 0; $i < $n; $i++)
        for($j = $i + 1; $j < $n; $j++)
            for($k = $j + 1; $k < $n; $k++)
                if(det($Point[$i][0], $Point[$i][1],
                       $Point[$j][0], $Point[$j][1],
                       $Point[$k][0], $Point[$k][1]))
                       $result = $result + 1;
 
    return $result;
}
 
// Driver code
$Point = array(array(0, 0),
               array(1, 1),
               array(2, 0),
               array(2, 2));
$n = count($Point);
echo countPoints($Point, $n);
 
// This code is contributed by
// mits
?>

<script>
 
// JavaScript program to count number
// of triangles that can be formed
// with given points in 2D
 
// Returns determinant value
// of three points in 2D
function det(x1, y1, x2, y2, x3, y3)
{
    return (x1 * (y2 - y3) -
            y1 * (x2 - x3) +
             1 * (x2 * y3 - y2 * x3));
}
   
// Returns count of possible
// triangles with given array
// of points in 2D.
function countPoints(Point, n)
{
     
    // Initialize result
    let result = 0;
   
    // Consider all triplets of
    // points given in inputs
    // Increment the result when
    // determinant of a triplet is not 0.
    for(let i = 0; i < n; i++)
        for(let j = i + 1; j < n; j++)
            for(let k = j + 1; k < n; k++)
                if (det(Point[i][0], Point[i][1],
                    Point[j][0], Point[j][1],
                    Point[k][0], Point[k][1]) >= 0)
                    result = result + 1;
   
    return result;
}
 
// Driver Code
let Point = [ [ 0, 0 ], [ 1, 1 ],
              [ 2, 0 ], [ 2, 2 ] ];
let n = Point.length;
 
document.write(countPoints(Point, n));
 
// This code is contributed by souravghosh0416
 
</script>

Producción: 

3

Tiempo Complejidad:  .

Optimización: 
Podemos optimizar la solución anterior para trabajar en O(n ² ) usando el hecho de que tres puntos no pueden formar un triángulo si son colineales. Podemos usar hashing para almacenar pendientes de todos los pares y encontrar todos los triángulos en tiempo O(n ² ).
Este artículo es una contribución de Vrushank Upadhyay . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.