Número total de arreglos de entrega a domicilio válidos

Dado el número de pedidos, encuentre el número de arreglos válidos de pedidos donde la entrega del i-ésimo pedido es siempre posterior a la recogida del i-ésimo pedido.

Ejemplos:

Entrada: N = 1
Salida: 1
Aquí, el evento total es 2. Son {P1, D1}.
¡El arreglo total posible es 2! = 2. [P1, D1] y [D1, P1].
Entonces, el único arreglo válido posible: [P1, D1].
[D1, P1] es un arreglo no válido ya que la entrega del primer pedido se realiza antes de la recogida del primer pedido.

Entrada: N = 2
Salida: 6
Aquí, el evento total es 4. Son {P1, D1, P2, D2}.
¡Aquí, el total de arreglos posibles es 4! = 24.
Entre ellos, 6 son arreglos válidos:
[P1, P2, D1, D2], [P1, D1, P2, D2], [P1, P2, D2, D1], [P2, P1, D2, D1] , [P2, P1, D1, D2] y [P2, D2, P1, D1].
El resto de todos son arreglos inválidos.
Algunos arreglos no válidos:
[P1, D1, D2, P2] – La entrega del segundo pedido se realiza antes de la recolección
[P2, D1, P1, D2] – La entrega del primer pedido se realiza antes de la recolección
[D1, D2, P2, P1] – La entrega de ambos pedidos es antes de la recogida.

Enfoque 1:

Considere N = 4, tenemos un total de 8 eventos.
Hay 4 eventos para recogida {P1, P2, P3, P4} y 4 eventos para entrega {D1, D2, D3, D4}.
Si consideramos solo los eventos de recogida, no hay restricciones en los arreglos entre recogidas. Entonces, ¡total de arreglos posibles 4!
Ahora consideramos la entrega. Partimos de la última recogida que hicimos.
- Para D4, podemos colocar D4 solo después de P4.
  Eso es P1, P2, P3, P4, __. Entonces solo hay 1 posición válida.
- Para D3, podemos colocar D3 en cualquiera de las siguientes posiciones.
  Son P1, P2, P3, __, P4, __, D4, __. Así que hay 3 posiciones válidas.
- Para D2, podemos colocar D2 en cualquiera de las siguientes posiciones.
  Son P1, P2, __, P3, __, P4, __, D4, __, D3 __. Así que 5 posiciones válidas.
- Para D1, podemos colocar D1 en cualquiera de las siguientes posiciones.
  Son P1, __, P2, __, P3, __, P4, __, D4, __, D3 __, D2, __. Entonces, 7 posiciones válidas.

Para cualquier N, arreglos válidos totales:
$N! * (1 * 3 * 5 * ... * (2 * N - 1))$

A continuación se muestra la implementación del enfoque anterior.

C++

// C++ implementation of the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find arrangements
int Arrangements(int N)
{
    int result = 1;
 
    for(int i = 1; i <= N; i++)
    {
       // Here, i for factorial and
       // (2*i-1) for series
       result = result * i * (2 * i - 1);
    }
    return result;
}
 
// Driver code
int main()
{
    int N = 4;
 
    cout << Arrangements(N);
 
    return 0;
}

Java

// Java implementation of the above approach
class GFG{
 
// Function to find arrangements
public static int Arrangements(int N)
{
    int result = 1;
     
    for(int i = 1; i <= N; i++)
    {
 
        // Here, i for factorial and
        // (2*i-1) for series
       result = result * i * (2 * i - 1);
    }
    return result;
}
 
// Driver code   
public static void main(String[] args)
{
    int N = 4;
     
    System.out.print(Arrangements(N));
}
}
 
// This code is contributed by divyeshrabadiya07

Python3

# Python3 implementation of the above approach
 
# Function to find arrangements
def Arrangements(N):
 
    result = 1
 
    for i in range(1, N + 1):
 
        # Here, i for factorial and
        # (2*i-1) for series
        result = result * i * (2 * i - 1)
 
    return result
 
# Driver code
N = 4;
print(Arrangements(N));
 
# This code is contributed by Akanksha_Rai

C#

// C# implementation of the above approach
using System;
 
class GFG{
     
// Function to find arrangements
public static int Arrangements(int N)
{
    int result = 1;
         
    for(int i = 1; i <= N; i++)
    {
 
       // Here, i for factorial and
       // (2*i-1) for series
       result = result * i * (2 * i - 1);
    }
    return result;
}
     
// Driver code
public static void Main(String[] args)
{
    int N = 4;
         
    Console.Write(Arrangements(N));
}
}
 
// This code is contributed by AnkitRai01

Javascript

<script>
 
// Javascript implementation of the above approach
 
// Function to find arrangements
function Arrangements(N)
{
    let result = 1;
 
    for(let i = 1; i <= N; i++)
    {
         
        // Here, i for factorial and
        // (2*i-1) for series
        result = result * i * (2 * i - 1);
    }
    return result;
}
 
// Driver code
let N = 4;
 
document.write(Arrangements(N));
 
// This code is contributed by _saurabh_jaiswal
 
</script>

Producción:

Complejidad de tiempo: O(N)
Complejidad de espacio auxiliar: O(1)

Enfoque 2:

Para N número de órdenes, tenemos $Total events = 2 * N$
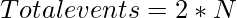
Así que el número total de arreglos posibles es $( 2 * N )!$
Ahora, cada pedido solo puede ser válido si la entrega es posterior a la recogida.

Para cada [Pi, Di], no podemos cambiar este arreglo, es decir, no podemos hacer [Di, Pi]. Solo hay un acuerdo válido para cada pedido. Así que tenemos que dividir por 2 para cada pedido. Así que el arreglo válido total es $( 2 * N )! / 2 ^ N$

A continuación se muestra la implementación del enfoque anterior.

C++

// C++ implementation of the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find arrangements
int Arrangements(int N)
{
    int result = 1;
 
    for (int i = 1; i <= 2 * N; i += 2)
        result = (result * i * (i + 1)) / 2;
 
    return result;
}
 
// Driver code
int main()
{
    int N = 4;
 
    cout << Arrangements(N);
 
    return 0;
}

Java

// Java implementation of the above approach
import java.util.*;
class GFG{
     
// Function to find arrangements
public static int Arrangements(int N)
{
    int result = 1;
 
    for (int i = 1; i <= 2 * N; i += 2)
        result = (result * i * (i + 1)) / 2;
 
    return result;
}
 
// Driver code
public static void main(String args[])
{
    int N = 4;
 
    System.out.print(Arrangements(N));
}
}
 
// This code is contributed by Code_Mech

Python3

# Python3 implementation of the above approach
 
# Function to find arrangements
def Arrangements(N):
    result = 1;
 
    for i in range(1, (2 * N) + 1, 2):
        result = (result * i * (i + 1)) / 2;
 
    return int(result);
 
# Driver code
if __name__ == '__main__':
    N = 4;
 
    print(Arrangements(N));
 
# This code is contributed by gauravrajput1

C#

// C# implementation of the above approach
using System;
class GFG{
     
// Function to find arrangements
public static int Arrangements(int N)
{
    int result = 1;
 
    for (int i = 1; i <= 2 * N; i += 2)
        result = (result * i * (i + 1)) / 2;
 
    return result;
}
 
// Driver code
public static void Main()
{
    int N = 4;
 
    Console.Write(Arrangements(N));
}
}
 
// This code is contributed by Code_Mech

Javascript

<script>
// Javascript implementation of the above approach
 
// Function to find arrangements
function Arrangements(N)
{
    var result = 1;
 
    for (var i = 1; i <= 2 * N; i += 2)
        result = parseInt( (result * i * (i + 1)) / 2);
 
    return result;
}
 
var  N = 4;
document.write( Arrangements(N));
 
 
// This code is contributed by SoumikMondal
</script>

Producción:

Complejidad de tiempo: O(N)
Complejidad de espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por animesh_ghosh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta