Optimización univariante: ciencia de datos

Wikipedia define la optimización como un problema en el que maximizas o minimizas una función real eligiendo sistemáticamente valores de entrada de un conjunto permitido y calculando el valor de la función. Eso significa que cuando hablamos de optimización siempre estamos interesados en encontrar la mejor solución. Entonces, digamos que uno tiene alguna forma funcional (por ejemplo, en la forma de f(x) ) y está tratando de encontrar la mejor solución para esta forma funcional. Ahora bien, ¿qué significa mejor? Uno podría decir que está interesado en minimizar esta forma funcional o maximizar esta forma funcional.
Generalmente, un problema de optimización tiene tres componentes.

minimizar f(x),
wrt x,
sujeto a a < x < b
donde, f(x) : Función objetivo
x : Variable de decisión
a < x < b : Restricción

Dependiendo de los tipos de restricciones, la optimización se puede clasificar en dos partes

Problemas de optimización con restricciones: en los casos en que la restricción se da allí y tenemos que tener una solución que satisfaga estas restricciones, los llamamos problemas de optimización con restricciones.
Problemas de optimización sin restricciones: en los casos en los que falta la restricción, los llamamos problemas de optimización sin restricciones.

¿Qué es la optimización univariante?
La optimización univariante es un caso simple de un problema de optimización no lineal con un caso sin restricciones, es decir, no hay ninguna restricción. La optimización univariante se puede definir como una optimización no lineal sin restricciones y solo hay una variable de decisión en esta optimización para la que estamos tratando de encontrar un valor.

mín f(x)
sobre x
x ∈ R

Entonces, cuando miras este problema de optimización, normalmente lo escribes en la forma anterior donde dices que vas a minimizar f(x) , y esta función se llama función objetivo. Y la variable que puede usar para minimizar esta función, que se llama la variable de decisión, se escribe a continuación así: wrt x aquí y también dice que x es continua, es decir, podría tomar cualquier valor en la línea de números reales. Y dado que este es un problema de optimización univariado, x es una variable escalar y no una variable vectorial.
Las condiciones necesarias y suficientes para que x sea el minimizador de la función f(x).
En el caso de optimización univariada, las condiciones necesarias y suficientes para que x sea el minimizador de la función f(x) son

Condición necesaria de primer orden: f'(x) = 0
Condición de suficiencia de segundo orden: f”(x) > 0

Resolvamos rápidamente un ejemplo numérico sobre esto para comprender mejor estas condiciones.

Ejemplo numérico:
min f(x) wrt x

Dado f(x) = 3x ⁴ – 4x ³ – 12x ² + 3

Según la condición necesaria de primer orden:
$\begin{array}{l} f^{\prime}(x)=0 \\ \Rightarrow 12 x^{3}-12 x^{2}-24 x=0 \\ \Rightarrow 12 x\left(x^{2}-x-2 x\right)=0 \\ \Rightarrow 12 x(x+1)(x-2)=0 \\ \text { e.g } x=0, x=-1, x=2 \end{array}$
Ahora, queremos saber entre estos 3 valores de x cuáles son en realidad minimizadores. Para ello nos fijamos en la condición de suficiencia de segundo orden. Entonces de acuerdo a la condición de suficiencia de segundo orden: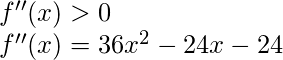
$\begin{array}{l} f^{\prime \prime}(x)>0 \\ f^{\prime \prime}(x)=36 x^{2}-24 x-24 \end{array}$
Poniendo cada valor de x en la ecuación anterior:
f”(x) | _{x = 0} = -24 (No cumple la condición de suficiencia)
f”(x) | _{x = -1} = 36 > 0 (Satisface la condición de suficiencia)
f”(x) | _{x = 2} = 72 > 0 (Satisface la condición de suficiencia)
Por lo tanto, -1 y 2 son el minimizador real de f(x). Así que para estos 2 valores
f(x) | _{x = -1} = -2
f(x) | _{x = 2} = -29

Publicación traducida automáticamente

Artículo escrito por AmiyaRanjanRout y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta