Programa para calcular el Área y el Perímetro de la Circunferencia de un Triángulo Equilátero

Dada la longitud de los lados de un triángulo equilátero, la tarea es encontrar el área y el perímetro de Incircle del triángulo equilátero dado.

Ejemplos:

Input: side = 6 
Output: Area = 9.4. Perimeter = 10.88

Input: side = 9
Output: Area = 21.21, Perimeter = 16.32

Las propiedades de un Incircle son:

El centro del Incircle es el mismo que el centro del triángulo, es decir, el punto donde se cruzan las medianas del triángulo equilátero.
La circunferencia inscrita de un triángulo equilátero se hace por el punto medio de las aristas de un triángulo equilátero.
El Inradius de un Incircle de un triángulo equilátero se puede calcular usando la fórmula:
```
 ,
```
donde $a$ es la longitud del lado del triángulo equilátero.
La imagen de abajo muestra un triángulo equilátero con incircunferencia:

Acercarse:

Área del círculo = 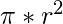$\pi*r^2$ y perímetro del círculo = 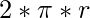$2 * \pi * r$ , donde r es el radio del círculo dado.

También el radio de Incircunferencia de un triángulo equilátero = (lado del triángulo equilátero)/ 3.
Por lo tanto,

La fórmula utilizada para calcular el área de Incircle usando Inradius es:
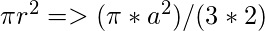
La fórmula utilizada para calcular el perímetro de Incircle usando Inradius es:

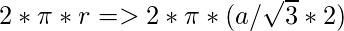
C

// C program to find the area of Inscribed circle 
// of equilateral triangle
#include <math.h>
#include <stdio.h>
#define PI 3.14159265
  
// function to find area of inscribed circle
float area_inscribed(float a)
{
    return (a * a * (PI / 12));
}
  
// function to find Perimeter of inscribed circle
float perm_inscribed(float a)
{
    return (PI * (a / sqrt(3)));
}
  
// Driver code
int main()
{
    float a = 6;
    printf("Area of inscribed circle is :%f\n",
           area_inscribed(a));
  
    printf("Perimeter of inscribed circle is :%f",
           perm_inscribed(a));
  
    return 0;
}

Java

// Java code to find the area of inscribed
// circle of equilateral triangle
import java.lang.*;
  
class GFG {
  
    static double PI = 3.14159265;
  
    // function to find the area of
    // inscribed circle
    public static double area_inscribed(double a)
    {
        return (a * a * (PI / 12));
    }
  
    // function to find the perimeter of
    // inscribed circle
    public static double perm_inscribed(double a)
    {
        return (PI * (a / Math.sqrt(3)));
    }
  
    // Driver code
    public static void main(String[] args)
    {
        double a = 6.0;
        System.out.println("Area of inscribed circle is :"
                           + area_inscribed(a));
  
        System.out.println("\nPerimeter of inscribed circle is :"
                           + perm_inscribed(a));
    }
}

Python3

# Python3 code to find the area of inscribed 
# circle of equilateral triangle
import math
PI = 3.14159265
      
# Function to find the area of 
# inscribed circle
def area_inscribed(a):
    return (a * a * (PI / 12))
  
# Function to find the perimeter of 
# inscribed circle
def perm_inscribed(a):
    return ( PI * (a / math.sqrt(3) ) )    
  
  
# Driver code
a = 6.0
print("Area of inscribed circle is :% f"
                        % area_inscribed(a))
print("\nPerimeter of inscribed circle is :% f"
                        % perm_inscribed(a))

C#

// C# code to find the area of
// inscribed circle
// of equilateral triangle
using System;
  
class GFG {
    static double PI = 3.14159265;
  
    // function to find the area of
    // inscribed circle
    public static double area_inscribed(double a)
    {
        return (a * a * (PI / 12));
    }
  
    // function to find the perimeter of
    // inscribed circle
    public static double perm_inscribed(double a)
    {
        return (PI * (a / Math.Sqrt(3)));
    }
  
    // Driver code
    public static void Main()
    {
        double a = 6.0;
        Console.Write("Area of inscribed circle is :"
                      + area_inscribed(a));
  
        Console.Write("\nPerimeter of inscribed circle is :"
                      + perm_inscribed(a));
    }
}

PHP

<?php
// PHP program to find the 
// area of inscribed 
// circle of equilateral triangle
$PI = 3.14159265;
  
// function to find area of 
// inscribed circle
function area_inscribed($a)
{
    global $PI;
    return ($a * $a * ($PI / 12));
}
  
// function to find perimeter of 
// inscribed circle
function perm_inscribed($a)
{
    global $PI;
    return ( $PI * ( $a / sqrt(3) ) );
}
  
// Driver code
$a = 6;
echo("Area of inscribed circle is :");
echo(area_inscribed($a));
echo("Perimeter of inscribed circle is :");
echo(perm_inscribed($a));
  
?>

Producción:

Area of inscribed circle is :9.424778
Perimeter of inscribed circle is :10.882796

Publicación traducida automáticamente

Artículo escrito por Krishna_Yadav y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C

Java

Python3

C#

PHP

Deja una respuesta Cancelar la respuesta