Programa para encontrar la suma de 1 + x/2! +x^2/3! +…+x^n/(n+1)!

Posted on by Rudeus Greyrat

Dado un número x y n, la tarea es encontrar la suma de la siguiente serie de x hasta n términos:  

1+\frac{x}{2!}+\frac{x^{2}}{3!}+..+\frac{x^{n}}{(n+1)!}

Ejemplos:  

Input: x = 5, n = 2
Output: 7.67
Explanation:
    Sum of first two termed
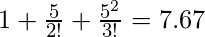    1+\frac{5}{2!}+\frac{5^{2}}{3!} = 7.67Input: x = 5, n = 4Output: 18.08Explanation: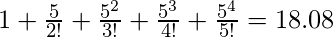1+\frac{5}{2!}+\frac{5^{2}}{3!}+\frac{5^{3}}{4!}+\frac{5^{4}}{5!} = 18.08

Enfoque: iterar el bucle hasta el término n, calcular la fórmula en cada iteración, es decir  

nth term of the series = \frac{x^{i}}{(i+1)!}

A continuación se muestra la implementación del enfoque anterior: 
 

C++

// C++ Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
 
#include <iostream>
#include <math.h>
using namespace std;
 
// Method to find the factorial of a number
int fact(int n)
{
    if (n == 1)
        return 1;
 
    return n * fact(n - 1);
}
 
// Method to compute the sum
double sum(int x, int n)
{
    double i, total = 1.0;
 
    // Iterate the loop till n
    // and compute the formula
    for (i = 1; i <= n; i++) {
        total = total + (pow(x, i) / fact(i + 1));
    }
 
    return total;
}
 
// Driver code
int main()
{
 
    // Get x and n
    int x = 5, n = 4;
 
    // Print output
    cout << "Sum is: " << sum(x, n);
 
    return 0;
}

Java

// Java Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
 
public class SumOfSeries {
 
    // Method to find factorial of a number
    static int fact(int n)
    {
        if (n == 1)
            return 1;
 
        return n * fact(n - 1);
    }
 
    // Method to compute the sum
    static double sum(int x, int n)
    {
        double total = 1.0;
 
        // Iterate the loop till n
        // and compute the formula
        for (int i = 1; i <= n; i++) {
            total = total + (Math.pow(x, i) / fact(i + 1));
        }
 
        return total;
    }
 
    // Driver Code
    public static void main(String[] args)
    {
 
        // Get x and n
        int x = 5, n = 4;
 
        // Find and print the sum
        System.out.print("Sum is: " + sum(x, n));
    }
}

Python3

# Python3 Program to compute sum of
# 1 + x / 2 ! + x ^ 2 / 3 ! +...+x ^ n/(n + 1)!
 
# Method to find the factorial of a number
def fact(n):
    if n == 1:
        return 1
    else:
        return n * fact(n - 1)
 
# Method to compute the sum
def sum(x, n):
    total = 1.0
 
    # Iterate the loop till n
    # and compute the formula
    for i in range (1, n + 1, 1):
        total = total + (pow(x, i) / fact(i + 1))
 
    return total
 
# Driver code
if __name__== '__main__':
     
    # Get x and n
    x = 5
    n = 4
 
    # Print output
    print ("Sum is: {0:.4f}".format(sum(x, n)))
     
# This code is contributed by
# SURENDRA_GANGWAR

C#

// C# Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
using System;
 
class SumOfSeries {
 
    // Method to find factorial of a number
    static int fact(int n)
    {
        if (n == 1)
            return 1;
 
        return n * fact(n - 1);
    }
 
    // Method to compute the sum
    static double sum(int x, int n)
    {
        double total = 1.0;
 
        // Iterate the loop till n
        // and compute the formula
        for (int i = 1; i <= n; i++) {
            total = total + (Math.Pow(x, i) / fact(i + 1));
        }
 
        return total;
    }
 
    // Driver Code
    public static void Main()
    {
 
        // Get x and n
        int x = 5, n = 4;
 
        // Find and print the sum
        Console.WriteLine("Sum is: " + sum(x, n));
    }
}
 
// This code is contributed
// by anuj_67..

PHP

<?php
// PHP Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
 
// Function to find the factorial
// of a number
function fact($n)
{
    if ($n == 1)
        return 1;
 
    return $n * fact($n - 1);
}
 
// Function to compute the sum
function sum($x, $n)
{
    $total = 1.0;
 
    // Iterate the loop till n
    // and compute the formula
    for ($i = 1; $i <= $n; $i++)
    {
        $total = $total + (pow($x, $i) /
                          fact($i + 1));
    }
 
    return $total;
}
 
// Driver code
 
// Get x and n
$x = 5;
$n = 4;
 
// Print output
echo "Sum is: ", sum($x, $n);
 
// This code is contributed by ANKITRAI1
?>

Javascript

<script>
// java script  Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
 
// Function to find the factorial
// of a number
function fact(n)
{
    if (n == 1)
        return 1;
 
    return n * fact(n - 1);
}
 
// Function to compute the sum
function sum(x, n)
{
    let total = 1.0;
 
    // Iterate the loop till n
    // and compute the formula
    for (let i = 1; i <= n; i++)
    {
        total = total + (Math.pow(x, i) /
                        fact(i + 1));
    }
 
    return total.toFixed(4);
}
 
// Driver code
 
// Get x and n
let x = 5;
let n = 4;
 
// Print output
document.write( "Sum is: "+ sum(x, n));
 
// This code is contributed by sravan kumar Gottumukkala
</script>
Producción: 

Sum is: 18.0833

 

Complejidad temporal: O(n 2 )

Espacio Auxiliar: O(n)

Enfoque eficiente: la complejidad del tiempo para el algoritmo anterior es O( n^{2} ) porque para cada iteración de suma se calcula el factorial, que es O(n). Se puede observar que el  i^{th} término de la serie se puede escribir como  S_i = (\frac{x}{i+1}) \cdot S_{i-1} , donde  S_0 = 1 . Ahora podemos iterar  i para calcular la suma.
A continuación se muestra la implementación del enfoque anterior:
 

C++

// C++ implementation of the approach
#include <iostream>
using namespace std;
 
// Function to compute the series sum
double sum(int x, int n)
{
    double total = 1.0;
 
    // To store the value of S[i-1]
    double previous = 1.0;
 
    // Iterate over n to store sum in total
    for (int i = 1; i <= n; i++)
    {
 
        // Update previous with S[i]
        previous = (previous * x) / (i + 1);
        total = total + previous;
    }
    return total;
}
 
// Driver code
int main()
{
    // Get x and n
    int x = 5, n = 4;
     
    // Find and print the sum
    cout << "Sum is: " << sum(x, n);
 
    return 0;
}
 
// This code is contributed by jit_t

Java

// Java implementation of the approach
 
public class GFG {
 
    // Function to compute the series sum
    static double sum(int x, int n)
    {
 
        double total = 1.0;
 
        // To store the value of S[i-1]
        double previous = 1.0;
 
        // Iterate over n to store sum in total
        for (int i = 1; i <= n; i++) {
 
            // Update previous with S[i]
            previous = (previous * x) / (i + 1);
            total = total + previous;
        }
 
        return total;
    }
 
    // Driver code
    public static void main(String[] args)
    {
 
        // Get x and n
        int x = 5, n = 4;
 
        // Find and print the sum
        System.out.print("Sum is: " + sum(x, n));
    }
}

Python3

# Python implementation of the approach
 
# Function to compute the series sum
def sum(x, n):
    total = 1.0;
 
    # To store the value of S[i-1]
    previous = 1.0;
 
    # Iterate over n to store sum in total
    for i in range(1, n + 1):
         
        # Update previous with S[i]
        previous = (previous * x) / (i + 1);
        total = total + previous;
 
    return total;
 
# Driver code
if __name__ == '__main__':
     
    # Get x and n
    x = 5;
    n = 4;
 
    # Find and print the sum
    print("Sum is: ", sum(x, n));
 
# This code is contributed by 29AjayKumar

C#

// C# implementation of the approach
using System;
 
class GFG
{
 
    // Function to compute the series sum
    public double sum(int x, int n)
    {
        double total = 1.0;
 
        // To store the value of S[i-1]
        double previous = 1.0;
 
        // Iterate over n to store sum in total
        for (int i = 1; i <= n; i++)
        {
 
            // Update previous with S[i]
            previous = ((previous * x) / (i + 1));
            total = total + previous;
        }
 
        return total;
    }
}
 
// Driver code
class geek
{
    public static void Main()
    {
        GFG g = new GFG();
 
        // Get x and n
        int x = 5, n = 4;
 
        // Find and print the sum
        Console.WriteLine("Sum is: " + g.sum(x, n));
    }
}
 
// This code is contributed by SoM15242

Javascript

<script>
    // Javascript implementation of the approach
     
    // Function to compute the series sum
    function sum(x, n)
    {
        let total = 1.0;
  
        // To store the value of S[i-1]
        let previous = 1.0;
  
        // Iterate over n to store sum in total
        for (let i = 1; i <= n; i++)
        {
  
            // Update previous with S[i]
            previous = ((previous * x) / (i + 1));
            total = total + previous;
        }
  
        return total;
    }
     
    // Get x and n
    let x = 5, n = 4;
 
    // Find and print the sum
    document.write("Sum is: " + sum(x, n));
     
</script>
Producción: 

Sum is: 18.083333333333336

 

Complejidad de tiempo: O(n)
Espacio auxiliar : O(1) ya que se usan variables constantes

Publicación traducida automáticamente

Artículo escrito por bilal-hungund y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *