Programa para encontrar si dos números y su AM y HM están presentes en una array usando STL

Dada una array de Número y dos valores A y B , la tarea es verificar las siguientes Condiciones:

1. Si dos números están presentes en la array o no.
2. En caso afirmativo, entonces su media aritmética y media armónica también están presentes en la misma array o no.
3. Si se cumplen todas las condiciones, imprima la media geométrica de los dos números.

Las respectivas medias de los números se pueden formular de la siguiente manera:
 

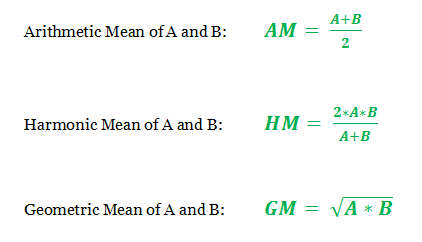
Ejemplos:

Entrada: arr[] = {1.0, 2.0, 2.5, 3.0, 4.0, 4.5, 5.0, 6.0}, A = 3, B = 6. 
Salida: GM = 4.24 
Explicación: 
A = 3, B = 6 están presentes en el formación. 
AM = 4.5, HM = 4 también están presentes en la array. 
Entonces, GM = 4.24
Entrada: arr = {1.0, 2.0, 2.5, 3.0, 4.0, 4.5, 5.0, 6.0}, A = 4, B = 6. 
Salida: AM y HM no encontrados

Acercarse:

• La idea es usar Hashing , mediante el cual podemos simplemente almacenar los elementos de la array en un contenedor Hash y usar operaciones O(1) de tiempo constante para encontrar y rastrear los números y sus medias. Finalmente, la media geométrica se calcula si se cumplen todas las condiciones observando la relación simple AM ​​* HM = GM ² .
• Una implementación paso a paso del enfoque anterior es la siguiente:
  1. Se define un contenedor Hash para almacenar los elementos de la array.
  2. Las medias aritméticas y armónicas se calculan en base a las fórmulas.
  3. Las declaraciones condicionales simples se utilizan para encontrar los elementos en el contenedor Hash en tiempo constante.
  4. Siempre que se cumplan todas las condiciones, el GM se calcula a partir de la relación anterior.

A continuación se muestra la implementación del enfoque anterior:

// C++ program to check if two numbers
// are present in an array then their
// AM and HM are also present. Finally,
// find the GM of the numbers
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the Arithmetic Mean
// of 2 numbers
float ArithmeticMean(float A, float B)
{
    return (A + B) / 2;
}
 
// Function to find the Harmonic Mean
// of 2 numbers
float HarmonicMean(float A, float B)
{
    return (2 * A * B) / (A + B);
}
 
// Following function checks and computes the
// desired results based on the means
void CheckArithmeticHarmonic(float arr[],
                             float A,
                             float B, int N)
{
     
    // Calculate means
    float AM = ArithmeticMean(A, B);
    float HM = HarmonicMean(A, B);
 
    // Hash container (Set) to store elements
    unordered_set<float> Hash;
 
    // Insertion of array elements in the Set
    for (int i = 0; i < N; i++)
    {
        Hash.insert(arr[i]);
    }
 
    // Conditionals to check if numbers
    // are present in array by Hashing
    if (Hash.find(A) != Hash.end()
        && Hash.find(B) != Hash.end()) {
 
        // Conditionals to check if the AM and HM
        // of the numbers are present in array
        if (Hash.find(AM) != Hash.end()
            && Hash.find(HM) != Hash.end()) {
           
            // If all conditions are satisfied,
            // the Geometric Mean is calculated
            cout << "GM = ";
            printf("%0.2f", sqrt(AM * HM));
        }
        else
        {
            // If numbers are found but the
            // respective AM and HM are not
            // found in the array
            cout << "AM and HM not found";
        }
    }
    else
    {
        // If none of the conditions are satisfied
        cout << "Numbers not found";
    }
}
 
int main()
{
   
    float arr[] = {1.0, 2.0, 2.5, 3.0, 4.0,
                   4.5, 5.0, 6.0};
 
    int N = sizeof(arr)/sizeof(arr[0]);
    float A = 3.0;
    float B = 6.0;
    CheckArithmeticHarmonic(arr, A, B, N);
    return 0;
}

// Java program to check if two numbers
// are present in an array then their
// AM and HM are also present. Finally,
// find the GM of the numbers
import java.util.*;
 
class GFG{
     
// Function to find the Arithmetic Mean
// of 2 numbers
static Double ArithmeticMean(Double A, Double B)
{
    return (A + B) / 2;
}
 
// Function to find the Harmonic Mean
// of 2 numbers
static Double HarmonicMean(Double A, Double B)
{
    return (2 * A * B) / (A + B);
}
 
// Following function checks and computes the
// desired results based on the means
static void CheckArithmeticHarmonic(Double arr[],
                                    Double A,
                                    Double B, int N)
{
 
    // Calculate means
    Double AM = ArithmeticMean(A, B);
    Double HM = HarmonicMean(A, B);
     
    // Hash container (HashMap) to store elements
    HashMap<Double,
            Integer> Hash = new HashMap<Double,
                                        Integer>();
     
    // Insertion of array elements in the Set
    for(int i = 0; i < N; i++)
    {
        Hash.put(arr[i], 1);
    }
     
    // Conditionals to check if numbers
    // are present in array by Hashing
    if (Hash.get(A) != 0 &&
        Hash.get(B) != 0)
    {
         
        // Conditionals to check if the AM and HM
        // of the numbers are present in array
        if (Hash.get(AM) != 0 &&
            Hash.get(HM) != 0)
        {
             
            // If all conditions are satisfied,
            // the Geometric Mean is calculated
            System.out.print("GM = ");
            System.out.format("%.2f", Math.sqrt(AM * HM));
        }
        else
        {
             
            // If numbers are found but the
            // respective AM and HM are not
            // found in the array
            System.out.print("AM and HM not found");
        }
    }
    else
    {
         
        // If none of the conditions are satisfied
        System.out.print("numbers not found");
    }
}
 
// Driver code
public static void main(String args[])
{
    Double arr[] = { 1.0, 2.0, 2.5, 3.0,
                     4.0, 4.5, 5.0, 6.0};
                      
    int N = (arr.length);
    Double A = 3.0;
    Double B = 6.0;
     
    CheckArithmeticHarmonic(arr, A, B, N);
}
}
 
// This code is contributed by Stream_Cipher   

# Python3 program to check if two numbers
# are present in an array then their
# AM and HM are also present. Finally,
# find the GM of the numbers
from math import sqrt
 
# Function to find the arithmetic mean
# of 2 numbers
def ArithmeticMean(A, B):
    return (A + B) / 2
 
# Function to find the harmonic mean
# of 2 numbers
def HarmonicMean(A, B):
    return (2 * A * B) / (A + B)
 
# Following function checks and computes the
# desired results based on the means
def CheckArithmeticHarmonic(arr, A, B, N):
     
    # Calculate means
    AM = ArithmeticMean(A, B)
    HM = HarmonicMean(A, B)
 
    # Hash container (set) to store elements
    Hash = set()
 
    # Insertion of array elements in the set
    for i in range(N):
        Hash.add(arr[i])
 
    # Conditionals to check if numbers
    # are present in array by Hashing
    if (A in Hash and B in Hash):
         
        # Conditionals to check if the AM and HM
        # of the numbers are present in array
        if (AM in Hash and HM in Hash):
             
            # If all conditions are satisfied,
            # the Geometric Mean is calculated
            print("GM =", round(sqrt(AM * HM), 2))
        else:
             
            # If numbers are found but the
            # respective AM and HM are not
            # found in the array
            print("AM and HM not found")
    else:
         
        # If none of the conditions are satisfied
        print("Numbers not found")
 
# Driver Code
if __name__ == '__main__':
 
    arr = [ 1.0, 2.0, 2.5, 3.0,
            4.0, 4.5, 5.0, 6.0 ]
    N = len(arr)
    A = 3.0
    B = 6.0
     
    CheckArithmeticHarmonic(arr, A, B, N)
 
# This code is contributed by Samarth

// C# program to check if two numbers
// are present in an array then their
// AM and HM are also present. Finally,
// find the GM of the numbers
using System;
using System.Collections.Generic;
 
class GFG{
     
// Function to find the Arithmetic Mean
// of 2 numbers
static Double ArithmeticMean(Double A, Double B)
{
    return (A + B) / 2;
}
 
// Function to find the Harmonic Mean
// of 2 numbers
static Double HarmonicMean(Double A, Double B)
{
    return (2 * A * B) / (A + B);
}
 
// Following function checks and computes the
// desired results based on the means
static void CheckArithmeticHarmonic(Double []arr,
                                    Double A,
                                    Double B, int N)
{
 
    // Calculate means
    Double AM = ArithmeticMean(A, B);
    Double HM = HarmonicMean(A, B);
     
    // Hash container (Set) to store elements
    // HashMap<Double,int> Hash = new HashMap<Double,int>();
    Dictionary<Double,
               int> Hash = new Dictionary<Double,
                                          int>();
     
    // Insertion of array elements in the Set
    for(int i = 0; i < N; i++)
    {
        Hash[arr[i]] = 1;
    }
     
    // Conditionals to check if numbers
    // are present in array by Hashing
    if (Hash.ContainsKey(A) &&
        Hash.ContainsKey(B))
    {
         
        // Conditionals to check if the AM and HM
        // of the numbers are present in array
        if (Hash.ContainsKey(AM) &&
            Hash.ContainsKey(HM))
        {
             
            // If all conditions are satisfied,
            // the Geometric Mean is calculated
            Console.Write("GM = ");
            Console.Write(Math.Round(
                          Math.Sqrt(AM * HM), 2));
        }
        else
        {
             
            // If numbers are found but the
            // respective AM and HM are not
            // found in the array
            Console.WriteLine("AM and HM not found");
        }
    }
    else
    {
         
        // If none of the conditions are satisfied
        Console.WriteLine("numbers not found");
    }
}
 
// Driver code
public static void Main()
{
    Double []arr = { 1.0, 2.0, 2.5, 3.0,
                     4.0, 4.5, 5.0, 6.0 };
 
    int N = (arr.Length);
    Double A = 3.0;
    Double B = 6.0;
     
    CheckArithmeticHarmonic(arr, A, B, N);
}
}
 
// This code is contributed by Stream_Cipher   

<script>
 
// Javascript program to check if two numbers
// are present in an array then their
// AM and HM are also present. Finally,
// find the GM of the numbers
 
// Function to find the Arithmetic Mean
// of 2 numbers
function ArithmeticMean(A, B)
{
    return ((A + B) / 2);
}
   
// Function to find the Harmonic Mean
// of 2 numbers
function HarmonicMean(A, B)
{
    return (2 * A * B) / (A + B);
}
   
// Following function checks and computes the
// desired results based on the means
function CheckArithmeticHarmonic(arr, A, B, N)
{
   
    // Calculate means
    let AM = ArithmeticMean(A, B);
    let HM = HarmonicMean(A, B);
       
    // Hash container (HashMap) to store elements
    let Hash = new Map();
       
    // Insertion of array elements in the Set
    for(let i = 0; i < N; i++)
    {
        Hash.set(arr[i], 1);
    }
       
    // Conditionals to check if numbers
    // are present in array by Hashing
    if (Hash.get(A) != 0 &&
        Hash.get(B) != 0)
    {
           
        // Conditionals to check if the AM and HM
        // of the numbers are present in array
        if (Hash.get(AM) != 0 &&
            Hash.get(HM) != 0)
        {
               
            // If all conditions are satisfied,
            // the Geometric Mean is calculated
            document.write("GM = ");
            document.write(Math.sqrt(AM * HM).toFixed(2));
        }
        else
        {
               
            // If numbers are found but the
            // respective AM and HM are not
            // found in the array
            document.write("AM and HM not found");
        }
    }
    else
    {
           
        // If none of the conditions are satisfied
        document.write("numbers not found");
    }
}
 
// Driver code
     
    let arr = [ 1.0, 2.0, 2.5, 3.0,
                     4.0, 4.5, 5.0, 6.0];
                        
    let N = (arr.length);
    let A = 3.0;
    let B = 6.0;
       
    CheckArithmeticHarmonic(arr, A, B, N);
      
     // This code is contributed by code_hunt.
</script>

GM = 4.24

Análisis de complejidad: 
la complejidad de tiempo general del programa anterior se basa en la iteración inicial de los elementos de la array en la entrada definida por el usuario. Las operaciones de búsqueda asociadas con el Conjunto son todas operaciones de tiempo constante O(1). Por lo tanto, la complejidad del programa es O(N) donde N es el tamaño del arreglo.