El trabajo más corto primero (SJF) o el trabajo más corto después , es una política de programación que selecciona el proceso de espera con el menor tiempo de ejecución para ejecutar a continuación. SJN es un algoritmo no preventivo.
- El trabajo más corto primero tiene la ventaja de tener un tiempo de espera promedio mínimo entre todos los algoritmos de programación .
- Es un algoritmo codicioso .
- Puede causar inanición si siguen llegando procesos más cortos. Este problema se puede resolver utilizando el concepto de envejecimiento.
- Es prácticamente inviable ya que el sistema operativo puede no conocer el tiempo de ráfaga y, por lo tanto, no puede clasificarlos. Si bien no es posible predecir el tiempo de ejecución, se pueden usar varios métodos para estimar el tiempo de ejecución de un trabajo, como un promedio ponderado de los tiempos de ejecución anteriores. SJF se puede utilizar en entornos especializados donde se dispone de estimaciones precisas del tiempo de ejecución.
Por ejemplo:
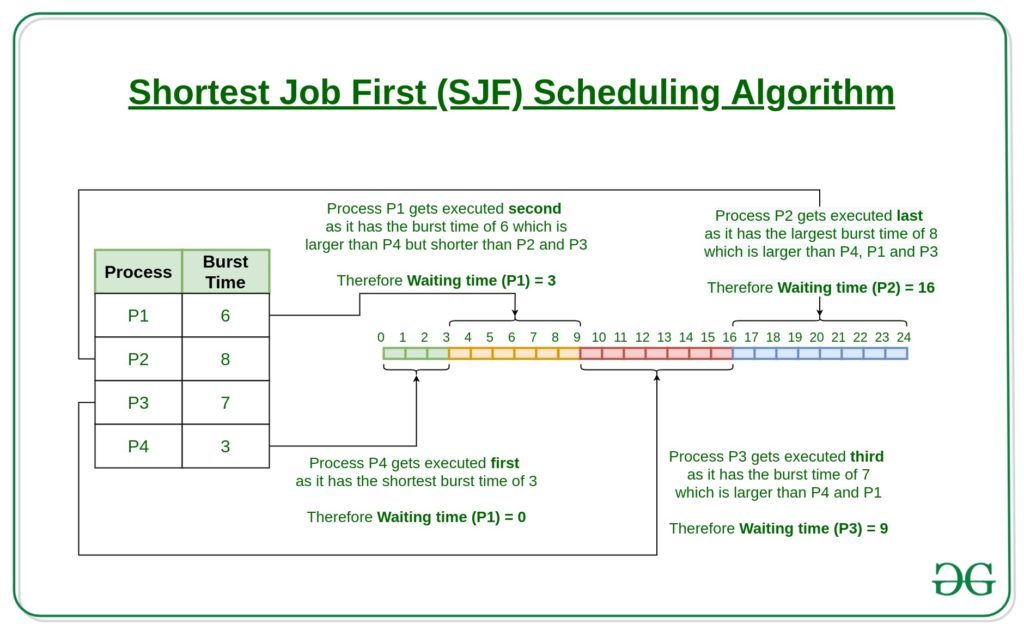
En el ejemplo anterior, dado que el tiempo de llegada de todos los procesos es 0, el orden de ejecución del proceso es el orden ascendente del tiempo de ráfaga de los procesos. El tiempo de ráfaga viene dado por la duración de la columna. Por tanto, el orden de ejecución de los procesos viene dado por:
P4 -> P1 -> P3 -> P2
Una implementación de este algoritmo ya se ha discutido en el artículo con la ayuda de Naive Approach . En este artículo, el algoritmo se implementa utilizando el concepto de un árbol de segmentos .
Enfoque: El siguiente es el enfoque utilizado para la implementación del trabajo más corto primero:
- Como sugiere el nombre, el primer algoritmo del trabajo más corto es un algoritmo que ejecuta el proceso cuyo tiempo de ráfaga es menor y ha llegado antes del tiempo actual. Por lo tanto, para encontrar el proceso que debe ejecutarse, ordene todos los procesos del conjunto dado de procesos de acuerdo con su hora de llegada. Esto asegura que el proceso con el tiempo de ráfaga más corto que haya llegado primero se ejecute primero.
- En lugar de encontrar el proceso de tiempo de ráfaga mínimo entre todos los procesos llegados mediante la iteración de
toda la array de estructuras, el rango mínimo del tiempo de ráfaga de todos los procesos llegados hasta el momento actual se calcula utilizando el árbol de segmentos . - Después de seleccionar un proceso que debe ejecutarse, el tiempo de finalización , el tiempo de respuesta y el tiempo de espera se calculan utilizando el tiempo de llegada y el tiempo de ráfaga del proceso. Las fórmulas para calcular los tiempos respectivos son:
- Hora de finalización: Hora en la que el proceso completa su ejecución.
- Hora de finalización: Hora en la que el proceso completa su ejecución.
Completion Time = Start Time + Burst Time
- Turn Around Time: Diferencia horaria entre la hora de finalización y la hora de llegada.
Turn Around Time = Completion Time – Arrival Time
- Tiempo de espera (WT): diferencia de tiempo entre el tiempo de respuesta y el tiempo de ráfaga.
Waiting Time = Turn Around Time – Burst Time
- Después del cálculo, los tiempos respectivos se actualizan en la array y el tiempo de ráfaga del proceso ejecutado se establece en infinito en la array base del árbol de segmentos para que no se considere como el tiempo de ráfaga mínimo en las consultas posteriores.
A continuación se muestra la implementación del trabajo más corto primero utilizando el concepto de árbol de segmentos :
C++
// C++ implementation of shortest job first
// using the concept of segment tree
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define z 1000000007
#define sh 100000
#define pb push_back
#define pr(x) printf("%d ", x)
struct util {
// Process ID
int id;
// Arrival time
int at;
// Burst time
int bt;
// Completion time
int ct;
// Turnaround time
int tat;
// Waiting time
int wt;
}
// Array to store all the process information
// by implementing the above struct util
ar[sh + 1];
struct util1 {
// Process id
int p_id;
// burst time
int bt1;
};
util1 range;
// Segment tree array to
// process the queries in nlogn
util1 tr[4 * sh + 5];
// To keep an account of where
// a particular process_id is
// in the segment tree base array
int mp[sh + 1];
// Comparator function to sort the
// struct array according to arrival time
bool cmp(util a, util b)
{
if (a.at == b.at)
return a.id < b.id;
return a.at < b.at;
}
// Function to update the burst time and process id
// in the segment tree
void update(int node, int st, int end,
int ind, int id1, int b_t)
{
if (st == end) {
tr[node].p_id = id1;
tr[node].bt1 = b_t;
return;
}
int mid = (st + end) / 2;
if (ind <= mid)
update(2 * node, st, mid, ind, id1, b_t);
else
update(2 * node + 1, mid + 1, end, ind, id1, b_t);
if (tr[2 * node].bt1 < tr[2 * node + 1].bt1) {
tr[node].bt1 = tr[2 * node].bt1;
tr[node].p_id = tr[2 * node].p_id;
}
else {
tr[node].bt1 = tr[2 * node + 1].bt1;
tr[node].p_id = tr[2 * node + 1].p_id;
}
}
// Function to return the range minimum of the burst time
// of all the arrived processes using segment tree
util1 query(int node, int st, int end, int lt, int rt)
{
if (end < lt || st > rt)
return range;
if (st >= lt && end <= rt)
return tr[node];
int mid = (st + end) / 2;
util1 lm = query(2 * node, st, mid, lt, rt);
util1 rm = query(2 * node + 1, mid + 1, end, lt, rt);
if (lm.bt1 < rm.bt1)
return lm;
return rm;
}
// Function to perform non_preemptive
// shortest job first and return the
// completion time, turn around time and
// waiting time for the given processes
void non_preemptive_sjf(int n)
{
// To store the number of processes
// that have been completed
int counter = n;
// To keep an account of the number
// of processes that have been arrived
int upper_range = 0;
// Current running time
int tm = min(INT_MAX, ar[upper_range + 1].at);
// To find the list of processes whose arrival time
// is less than or equal to the current time
while (counter) {
for (; upper_range <= n;) {
upper_range++;
if (ar[upper_range].at > tm || upper_range > n) {
upper_range--;
break;
}
update(1, 1, n, upper_range,
ar[upper_range].id, ar[upper_range].bt);
}
// To find the minimum of all the running times
// from the set of processes whose arrival time is
// less than or equal to the current time
util1 res = query(1, 1, n, 1, upper_range);
// Checking if the process has already been executed
if (res.bt1 != INT_MAX) {
counter--;
int index = mp[res.p_id];
tm += (res.bt1);
// Calculating and updating the array with
// the current time, turn around time and waiting time
ar[index].ct = tm;
ar[index].tat = ar[index].ct - ar[index].at;
ar[index].wt = ar[index].tat - ar[index].bt;
// Update the process burst time with
// infinity when the process is executed
update(1, 1, n, index, INT_MAX, INT_MAX);
}
else {
tm = ar[upper_range + 1].at;
}
}
}
// Function to call the functions and perform
// shortest job first operation
void execute(int n)
{
// Sort the array based on the arrival times
sort(ar + 1, ar + n + 1, cmp);
for (int i = 1; i <= n; i++)
mp[ar[i].id] = i;
// Calling the function to perform
// non-preemptive-sjf
non_preemptive_sjf(n);
}
// Function to print the required values after
// performing shortest job first
void print(int n)
{
cout << "ProcessId "
<< "Arrival Time "
<< "Burst Time "
<< "Completion Time "
<< "Turn Around Time "
<< "Waiting Time\n";
for (int i = 1; i <= n; i++) {
cout << ar[i].id << " \t\t "
<< ar[i].at << " \t\t "
<< ar[i].bt << " \t\t "
<< ar[i].ct << " \t\t "
<< ar[i].tat << " \t\t "
<< ar[i].wt << " \n";
}
}
// Driver code
int main()
{
// Number of processes
int n = 5;
// Initializing the process id
// and burst time
range.p_id = INT_MAX;
range.bt1 = INT_MAX;
for (int i = 1; i <= 4 * sh + 1; i++) {
tr[i].p_id = INT_MAX;
tr[i].bt1 = INT_MAX;
}
// Arrival time, Burst time and ID
// of the processes on which SJF needs
// to be performed
ar[1].at = 1;
ar[1].bt = 7;
ar[1].id = 1;
ar[2].at = 2;
ar[2].bt = 5;
ar[2].id = 2;
ar[3].at = 3;
ar[3].bt = 1;
ar[3].id = 3;
ar[4].at = 4;
ar[4].bt = 2;
ar[4].id = 4;
ar[5].at = 5;
ar[5].bt = 8;
ar[5].id = 5;
execute(n);
// Print the calculated time
print(n);
}
Java
// Java implementation of shortest job first
// using the concept of segment tree
import java.util.*;
class GFG {
static int z = 1000000007;
static int sh = 100000;
static class util {
// Process ID
int id;
// Arrival time
int at;
// Burst time
int bt;
// Completion time
int ct;
// Turnaround time
int tat;
// Waiting time
int wt;
}
// Array to store all the process information
// by implementing the above struct util
static util[] ar = new util[sh + 1];
static {
for (int i = 0; i < sh + 1; i++) {
ar[i] = new util();
}
}
static class util1 {
// Process id
int p_id;
// burst time
int bt1;
};
static util1 range = new util1();
// Segment tree array to
// process the queries in nlogn
static util1[] tr = new util1[4 * sh + 5];
static {
for (int i = 0; i < 4 * sh + 5; i++) {
tr[i] = new util1();
}
}
// To keep an account of where
// a particular process_id is
// in the segment tree base array
static int[] mp = new int[sh + 1];
// Comparator function to sort the
// struct array according to arrival time
// Function to update the burst time and process id
// in the segment tree
static void update(int node, int st, int end,
int ind, int id1, int b_t)
{
if (st == end) {
tr[node].p_id = id1;
tr[node].bt1 = b_t;
return;
}
int mid = (st + end) / 2;
if (ind <= mid)
update(2 * node, st, mid, ind, id1, b_t);
else
update(2 * node + 1, mid + 1, end, ind, id1, b_t);
if (tr[2 * node].bt1 < tr[2 * node + 1].bt1) {
tr[node].bt1 = tr[2 * node].bt1;
tr[node].p_id = tr[2 * node].p_id;
} else {
tr[node].bt1 = tr[2 * node + 1].bt1;
tr[node].p_id = tr[2 * node + 1].p_id;
}
}
// Function to return the range minimum of the burst time
// of all the arrived processes using segment tree
static util1 query(int node, int st, int end,
int lt, int rt)
{
if (end < lt || st > rt)
return range;
if (st >= lt && end <= rt)
return tr[node];
int mid = (st + end) / 2;
util1 lm = query(2 * node, st, mid, lt, rt);
util1 rm = query(2 * node + 1, mid + 1, end, lt, rt);
if (lm.bt1 < rm.bt1)
return lm;
return rm;
}
// Function to perform non_preemptive
// shortest job first and return the
// completion time, turn around time and
// waiting time for the given processes
static void non_preemptive_sjf(int n) {
// To store the number of processes
// that have been completed
int counter = n;
// To keep an account of the number
// of processes that have been arrived
int upper_range = 0;
// Current running time
int tm = Math.min(Integer.MAX_VALUE, ar[upper_range + 1].at);
// To find the list of processes whose arrival time
// is less than or equal to the current time
while (counter != 0) {
for (; upper_range <= n;) {
upper_range++;
if (ar[upper_range].at > tm || upper_range > n) {
upper_range--;
break;
}
update(1, 1, n, upper_range, ar[upper_range].id,
ar[upper_range].bt);
}
// To find the minimum of all the running times
// from the set of processes whose arrival time is
// less than or equal to the current time
util1 res = query(1, 1, n, 1, upper_range);
// Checking if the process has already been executed
if (res.bt1 != Integer.MAX_VALUE) {
counter--;
int index = mp[res.p_id];
tm += (res.bt1);
// Calculating and updating the array with
// the current time, turn around time and waiting time
ar[index].ct = tm;
ar[index].tat = ar[index].ct - ar[index].at;
ar[index].wt = ar[index].tat - ar[index].bt;
// Update the process burst time with
// infinity when the process is executed
update(1, 1, n, index, Integer.MAX_VALUE, Integer.MAX_VALUE);
} else {
tm = ar[upper_range + 1].at;
}
}
}
// Function to call the functions and perform
// shortest job first operation
static void execute(int n) {
// Sort the array based on the arrival times
Arrays.sort(ar, 1, n, new Comparator<util>() {
public int compare(util a, util b) {
if (a.at == b.at)
return a.id - b.id;
return a.at - b.at;
}
});
for (int i = 1; i <= n; i++)
mp[ar[i].id] = i;
// Calling the function to perform
// non-preemptive-sjf
non_preemptive_sjf(n);
}
// Function to print the required values after
// performing shortest job first
static void print(int n) {
System.out.println("ProcessId Arrival Time Burst Time" +
" Completion Time Turn Around Time Waiting Time");
for (int i = 1; i <= n; i++) {
System.out.printf("%d\t\t%d\t\t%d\t\t%d\t\t%d\t\t%d\n",
ar[i].id, ar[i].at, ar[i].bt, ar[i].ct, ar[i].tat,
ar[i].wt);
}
}
// Driver Code
public static void main(String[] args)
{
// Number of processes
int n = 5;
// Initializing the process id
// and burst time
range.p_id = Integer.MAX_VALUE;
range.bt1 = Integer.MAX_VALUE;
for (int i = 1; i <= 4 * sh + 1; i++)
{
tr[i].p_id = Integer.MAX_VALUE;
tr[i].bt1 = Integer.MAX_VALUE;
}
// Arrival time, Burst time and ID
// of the processes on which SJF needs
// to be performed
ar[1].at = 1;
ar[1].bt = 7;
ar[1].id = 1;
ar[2].at = 2;
ar[2].bt = 5;
ar[2].id = 2;
ar[3].at = 3;
ar[3].bt = 1;
ar[3].id = 3;
ar[4].at = 4;
ar[4].bt = 2;
ar[4].id = 4;
ar[5].at = 5;
ar[5].bt = 8;
ar[5].id = 5;
execute(n);
// Print the calculated time
print(n);
}
}
// This code is contributed by
// sanjeev2552
ProcessId Arrival Time Burst Time Completion Time Turn Around Time Waiting Time 1 1 7 8 7 0 2 2 5 16 14 9 3 3 1 9 6 5 4 4 2 11 7 5 5 5 8 24 19 11
Complejidad del tiempo: para analizar el tiempo de ejecución del algoritmo anterior, primero se deben comprender los siguientes tiempos de ejecución:
- La complejidad de tiempo para construir un árbol de segmentos para N procesos es O(N) .
- La complejidad del tiempo para actualizar un Node en un árbol de segmentos viene dada por O(log(N)) .
- La complejidad de tiempo para realizar una consulta de rango mínimo en un árbol de segmento viene dada por O(log(N)) .
- Dado que la operación de actualización y las consultas se realizan para N procesos dados, la complejidad temporal total del algoritmo es O(N*log(N)) donde N es el número de procesos.
- Este algoritmo funciona mejor que el enfoque mencionado en este artículo porque requiere O(N 2 ) para su ejecución.
Publicación traducida automáticamente
Artículo escrito por shubham763116 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA