Prerrequisitos – Prueba de hipótesis , valor p
Una prueba t es un tipo de estadística inferencial utilizada para determinar si existe una diferencia significativa entre las medias de dos grupos, que pueden estar relacionadas en ciertas características.
![]()
Si el valor t es grande => los dos grupos pertenecen a grupos diferentes.
Si el valor t es pequeño => los dos grupos pertenecen al mismo grupo.
Terminologías involucradas
- Grado de libertad (df) – Nos dice el número de variables independientes utilizadas para calcular la estimación entre 2 grupos de muestra. [Eq-2]
![]()
where, df = degree of freedom nS = size of the sample S
Supongamos que tenemos 2 muestras A y B. El df se calcularía como
gl = (n A -1) + (n B -1)
- Nivel de significancia (α) – Es la probabilidad de rechazar la hipótesis nula cuando es verdadera. En términos más simples, nos habla del porcentaje de riesgo que implica decir que existe una diferencia entre dos grupos, cuando en realidad no es así.
Hay tres tipos de pruebas t, y se clasifican como pruebas t dependientes e independientes.
- Prueba t de muestras independientes: compara las medias de dos grupos.
- Prueba t de muestras pareadas: compara las medias del mismo grupo en diferentes momentos (por ejemplo, con un año de diferencia).
- Prueba t de una muestra: la media de un solo grupo contra una media conocida.
1. Prueba t de muestra independiente
La prueba t de muestra independiente, comúnmente conocida como prueba t de muestra no pareada, se usa para averiguar si las diferencias encontradas entre dos grupos son realmente significativas o solo una ocurrencia aleatoria.
Podemos usar esto cuando:
- se desconoce la media o desviación estándar de la población. (se desconoce la información sobre la población)
- las dos muestras son separadas/independientes. Por ej. niños y niñas (los dos son independientes entre sí)
Fórmula utilizada:
![Rendered by QuickLaTeX.com t=\frac{\mu_{A}-\mu_{B}}{\sqrt{\left[\frac{1}{n_{A}}+\frac{1}{n_{B}}\right] *\left[\left(\sum A^{2}-\frac{\left(\sum A\right)^{2}}{n_{A}}\right)+\left(\sum B^{2}-\frac{\left(\sum B\right)^{2}}{n_{B}}\right)\right] *\left[\frac{1}{d f}\right]}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d60ad607d830b9645983c3ff36889091_l3.png)
where, t = t-value A = Sample of A B = Sample of B μA = Mean of sample A μB = Mean of sample B nA = samele size of A nB = sample size of B df = degree of freedom
Pasos involucrados
Step 1 - Find the sum of all values in each sample. Step 2 - Square the sum values found in step 1. Step 3 - Find the sum of square of individual values in each sample. Step 4 - Calculate the mean of each sample. Step 5 - Find the degree of freedom (df) using Eq-2. Step 6 - Insert all the values found in Steps 1-4 into Eq-3 and find the calculated t-value. Step 7 - Use the values of df and α (take α = 0.05 if not given) in the two-tails t-table (Click here) to find the table value of t. Step 8 - Compare values of t found in Step-6 and Step-7.
Interpretación de los resultados
If tcal > ttable=> p < (α=0.05) => significant difference between two groups found. If tcal < ttable => p > (α=0.05) => no significant difference between two groups.
Problema de ejemplo (paso a paso)
Supongamos que se dan dos datos de muestra independientes A y B, con los siguientes valores. Tenemos que realizar la prueba t de muestras independientes para estos datos.
|
Muestra A |
Muestra B |
|---|---|
|
1 |
1 |
|
2 |
2 |
|
4 |
2 |
|
4 |
3 |
|
5 |
3 |
|
5 |
4 |
|
6 |
5 |
|
7 |
6 |
|
8 |
7 |
|
8 |
7 |
Step 1 - ∑A = 1 + 2 + 4 + 4 + 5 + 5 + 6 + 7 + 8 + 8 = 50 ∑B = 1 + 2 + 2 + 3 + 3 + 4 + 5 + 6 + 7 + 7 = 40
Step 2 - (∑A)2 = (50)2 = 2500 (∑B)2 = (40)2 = 1600
Step 3 - ∑A2 = 12 + 22 + 42 + 42 + 52 + 52 + 62 + 72 + 82 + 82 = 300 ∑B2 = 12 + 22 + 22 + 32 + 32 + 42 + 52 + 62 + 72 + 72 = 202
Step 4 - n = 10 μA = (∑A / n) = 50/10 = 5 μB = (∑B / n) = 40/10 = 4
Step 5 - df = (nA - 1) + (nB - 1) = (10-1) + (10-1) = 18 [using Eq-2]
Step 6 - Putting values found in Eq-3 to find the calculated value of t.
we get, tcal = 0.99
Step 7 - Let value of α = 0.05 and df = 18. Looking up the two-tailed t-table.
(See table below or refer link above)
we get, ttable = 2.10
| (df)/(a) | 0.2 | 0.10 | 0.05 | . . |
|---|---|---|---|---|
|
∞ |
1.282 | 1.645 | 1.960 | . . |
|
1 |
3.078 | 6.314 | 12.706 | . . |
|
2 |
1.886 | 2.920 | 4.303 | . . |
|
: |
: | : | : | . . |
|
8 |
1.397 | 1.860 | 2.306 | . . |
|
9 |
1.383 | 1.833 | 2.262 | . . |
|
: |
: |
: |
: |
. . |
|
18 |
1.330 |
1.734 |
2.101 |
. . |
|
19 |
1.328 |
1.729 |
2.093 |
. . |
|
20 |
1.325 |
1.725 |
2.086 |
. . |
|
: |
: |
: |
: |
. . |
Step 8 - 0.99 < 2.10 (tcal < ttable by 1.11) => no significant difference found between two groups.
2. Prueba t de muestras pareadas
La prueba t de muestras pareadas, comúnmente conocida como prueba t de muestras dependientes, se usa para averiguar si la diferencia en la media de dos muestras es 0. La prueba se realiza en muestras dependientes, generalmente enfocándose en un grupo particular de personas o cosas. En esto, cada entidad se mide dos veces, lo que da como resultado un par de observaciones.
Podemos usar esto cuando:
- Se dan dos muestras similares (similares a gemelas). [Ej. Puntajes obtenidos en Inglés y Matemáticas (ambas materias)]
- La variable dependiente (datos) es continua.
- Las observaciones son independientes entre sí.
- La variable dependiente tiene una distribución aproximadamente normal.
Fórmula utilizada
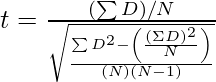
where, t = t-value D = difference between the two samples (A-B) N = sample size (same as n)
Pasos involucrados
Step 1 - Find the sum of difference of each two samples in data. [∑D = ∑(A-B)] Step 2 - Find the sum of square of each D found in Step 1. [(∑D2)] Step 3 - Find the square of summation of D. [(∑D)2] Step 4 - Put the values found from Steps 1-3 in Eq-4 and find the t-value. Step 5 - Find the degree of freedom (df) using Eq-2.
NOTA: Aquí, df se calcula como un todo para los datos, no para cada conjunto de muestras individual. Esto se debe a que las dos muestras A y B son gemelas. (similar)
Entonces gl = ∑(n S – 1) = N-1
Step 6 - Use the values of df and α (take α = 0.05 if not given) in the two-tails t-table (Click here) to find the table value of t. Step 7 - Compare values of t found in Step-4 and Step-6.
Interpretación de resultados
Igual que la prueba t de muestras independientes.
Problema de ejemplo (paso a paso)
Considere el siguiente ejemplo. Se toman las puntuaciones (sobre 25) de las materias Matemáticas y SST para una muestra de 10 alumnos. Tenemos que realizar la prueba t de muestra pareada para estos datos.
|
estudiante nro. |
Matemáticas |
acero inoxidable |
Paso 1 |
Paso 2 |
|---|---|---|---|---|
| 1 | 4 | 15 |
-11 |
121 |
| 2 | 4 | dieciséis |
-12 |
144 |
| 3 | 7 | 14 |
-7 |
49 |
| 4 | dieciséis | 14 |
2 |
4 |
| 5 | 20 | 22 |
-2 |
4 |
| 6 | 11 | 22 |
-11 |
121 |
| 7 | 13 | 23 |
-10 |
100 |
| 8 | 9 | 18 |
-9 |
81 |
| 9 | 11 | 18 |
-7 |
49 |
| 10 | 15 | 19 |
-4 |
dieciséis |
| Suma – | (∑D) = -71 | ∑D 2 = 689 |
Step 1 and Step 2 - as shown in table above.
Step 3 - (∑D)2 = (71)2 = 5041
Step 4 - Putting values in Eq-4, we get
tcal = -4.96
Step 5 - df = n -1 = 10 - 1 = 9
Step 6 - Using df = 9 and α = 0.05 in table. We get,
ttable = 2.26
Step 7 - -4.96 < 2.26 (tcal < ttable by 7.22) => no significant difference found between two groups.
3. Prueba t de una muestra
Una prueba t de muestra es una de las pruebas t ampliamente utilizadas para comparar la media muestral de los datos con un valor determinado. Se utiliza para comparar la media de la muestra con la media real/poblacional.
Podemos usar esto cuando:
el tamaño de la muestra es pequeño. (menores de 30) los datos se recopilan aleatoriamente. los datos tienen una distribución aproximadamente normal.
Fórmula utilizada:
where, t = t-value x_bar = sample mean μ = true/population mean σ = standard deviation n = sample size
Pasos involucrados
Step 1 - Define the null (h0) and alternative (h1) hypothesis.
Step 2 - Calculate sample mean. (if not given)
[population mean, standard deviation, n is given]
Step 3 - Put the values found in Step 1 into Eq-5 and calculate t-value. (tcal)
Step 4 - Calculate degree of freedom (df). (same as done in paired sample t-test)
Step 5 - Take α = 0.05 if not given. Use the value of df and α and find ttablefrom one tailed t-table. (Click here)
Step 6 - Compare values of t found in Step-3 and Step-5.
Interpretación de resultados
Igual que la prueba t de muestras independientes.
Problema de ejemplo (paso a paso)
Considere el siguiente ejemplo. Se tomaron los pesos de 25 personas obesas antes de inscribirlas en el campamento de nutrición. Se encuentra que el peso medio de la población es de 45 kg antes de iniciar el campamento. Después de terminar el campamento, para las mismas 25 personas, se encontró que la media de la muestra era 75 con una desviación estándar de 25. ¿Funcionó el campamento de acondicionamiento físico?
Step 1 - h0 -> μ = 45 (sample mean is true mean)
h1 -> μ ≠ 45 (sample mean is not true mean)
Step 2 - Given,
x_bar = 75
μ = 45
σ = 25
n = 25
Step 3 - Putting the values from Step 2 in Eq-5. we get,
tcal = 6
Step 4 - df = n - 1 = 24
Step 5 - Using df = 24 and α = 0.05 in table. We get,
ttable = 1.711
Step 6 - 6 > 1.711 (tcal > ttable) => significant difference found between two groups. => the nutrition camp significantly impacted the weights and it was a success.
Los tipos de pruebas t discutidos anteriormente son ampliamente utilizados en los campos de investigación en hospitales por expertos para obtener información importante sobre los datos médicos que se les brindan sobre los efectos de varios medicamentos y drogas en la población y les ayuda a extraer inferencias importantes con respecto a la mismo. Sin embargo, es responsabilidad de la persona ver qué prueba t produciría los mejores resultados y que se cumplan todos los supuestos de esa prueba t. Para cualquier duda/consulta, comenta abajo.
Publicación traducida automáticamente
Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA