Conteo de grupos entre N personas que tienen solo un líder en cada grupo

Posted on by Rudeus Greyrat

Dado un número N de personas, la tarea es contar el número de formas de formar grupos de tamaño ? N donde, en cada grupo, el primer elemento del grupo es el líder del grupo.
Nota:

  • Los grupos con las mismas personas que tienen diferentes líderes se tratan como un grupo diferente. Por ejemplo: el grupo {1, 2, 3} y {2, 1, 3} se tratan como grupos diferentes ya que tienen diferentes líderes 1 y 2 respectivamente.
  • Los grupos con el mismo líder y las mismas personas se tratan como un mismo grupo. Por ejemplo: los grupos {1, 3, 2} y {1, 2, 3} se tratan como el mismo grupo ya que tienen el mismo líder y las mismas personas.
  • La respuesta puede ser muy grande, lleve el módulo a (1e9+7).

Ejemplos:

Entrada: N = 3 
Salida: 12 
Explicación: 
Total Los grupos con líderes son: 
Grupos con líder 1: 
1. {1} 
2. {1, 2} 
3. {1, 3} 
4. {1, 2, 3} 
Grupos con Líder 2: 
5. {2} 
6. {2, 1} 
7. {2, 3} 
8. {2, 1, 3} 
Grupos con Líder 3: 
9. {3} 
10. {3, 1} 
11 {3, 2} 
12. {3, 1, 2}
Entrada: N = 5 
Salida: 80

Enfoque: Este problema se puede resolver utilizando el concepto de coeficientes binomiales y exponenciación modular . A continuación se presentan las observaciones a este enunciado del problema:

  • El número de formas de seleccionar un líder entre N personas es C(N, 1) .
  • Para cada líder podemos seleccionar un grupo de tamaño K donde 0 ≤ K ≤ N-1 para hacer el número posible de agrupamientos.
  • Entonces, el número total de formas viene dado por el producto de N y la suma de los elementos de selección K de los elementos restantes (N – 1) como:

    Vías Totales = \binom{N}{1} * \left ( \binom{N-1}{0} + \binom{N-1}{1} + \binom{N-1}{2} + ... + \ binom{N-1}{N-1} \right )

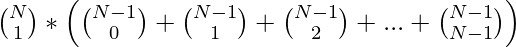
Usando el teorema binomial, la suma del coeficiente binomial se puede escribir como:

\binom{N}{1} * \left ( \binom{N-1}{0} + \binom{N-1}{1} + \binom{N-1}{2} + ... + \binom{N-1}{N-1} \right ) = 2^{N-1}

Por lo tanto, el número de formas de seleccionar grupos que tienen un solo líder es

N * 2^{N - 1}

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
  
#include <bits/stdc++.h>
using namespace std;
  
long long mod = 1000000007;
  
// Function to find 2^x using
// modular exponentiation
int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;
  
    // If B is even
    long long y;
    if (B % 2 == 0) {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }
  
    // If B is odd
    else {
        y = A % mod;
        y = (y * exponentMod(A, B - 1)
             % mod)
            % mod;
    }
  
    return (int)((y + mod) % mod);
}
  
// Function to count the number of
// ways to form the group having
// one leader
void countWays(int N)
{
  
    // Find 2^(N-1) using modular
    // exponentiation
    long long select = exponentMod(2,
                                   N - 1);
  
    // Count total ways
    long long ways
        = ((N % mod)
           * (select % mod));
  
    ways %= mod;
  
    // Print the total ways
    cout << ways;
}
  
// Driver Code
int main()
{
  
    // Given N number of peoples
    int N = 5;
  
    // Function Call
    countWays(N);
}

Java

// Java program for the above approach
import java.util.*;
class GFG{
  
static long mod = 1000000007;
  
// Function to find 2^x using
// modular exponentiation
static int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;
  
    // If B is even
    long y;
    if (B % 2 == 0) 
    {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }
  
    // If B is odd
    else 
    {
        y = A % mod;
        y = (y * exponentMod(A, B - 1) % 
                                  mod) % mod;
    }
  
    return (int)((y + mod) % mod);
}
  
// Function to count the number of
// ways to form the group having
// one leader
static void countWays(int N)
{
  
    // Find 2^(N-1) using modular
    // exponentiation
    long select = exponentMod(2, N - 1);
  
    // Count total ways
    long ways = ((N % mod) * (select % mod));
  
    ways %= mod;
  
    // Print the total ways
    System.out.print(ways);
}
  
// Driver Code
public static void main(String[] args)
{
  
    // Given N number of peoples
    int N = 5;
  
    // Function Call
    countWays(N);
}
}
  
// This code is contributed by sapnasingh4991

Python3

# Python3 program for the above approach
mod = 1000000007
  
# Function to find 2^x using
# modular exponentiation
def exponentMod(A, B):
      
    # Base cases
    if (A == 0):
        return 0;
    if (B == 0):
        return 1;
  
    # If B is even
    y = 0;
      
    if (B % 2 == 0):
        y = exponentMod(A, B // 2);
        y = (y * y) % mod;
  
    # If B is odd
    else:
        y = A % mod;
        y = (y * exponentMod(A, B - 1) %
                                  mod) % mod;
                               
    return ((y + mod) % mod);
  
# Function to count the number of
# ways to form the group having
# one leader
def countWays(N):
      
    # Find 2^(N-1) using modular
    # exponentiation
    select = exponentMod(2, N - 1);
  
    # Count total ways
    ways = ((N % mod) * (select % mod));
  
    ways %= mod;
  
    # Print the total ways
    print(ways)
      
# Driver code        
if __name__=='__main__':
      
    # Given N number of people
    N = 5;
  
    # Function call
    countWays(N);
  
# This code is contributed by rutvik_56

C#

// C# program for the above approach
using System;
class GFG{
   
static long mod = 1000000007;
   
// Function to find 2^x using
// modular exponentiation
static int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;
   
    // If B is even
    long y;
    if (B % 2 == 0) 
    {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }
   
    // If B is odd
    else
    {
        y = A % mod;
        y = (y * exponentMod(A, B - 1) % 
                                  mod) % mod;
    }
   
    return (int)((y + mod) % mod);
}
   
// Function to count the number of
// ways to form the group having
// one leader
static void countWays(int N)
{
   
    // Find 2^(N-1) using modular
    // exponentiation
    long select = exponentMod(2, N - 1);
   
    // Count total ways
    long ways = ((N % mod) * (select % mod));
   
    ways %= mod;
   
    // Print the total ways
    Console.Write(ways);
}
   
// Driver Code
public static void Main(String[] args)
{
   
    // Given N number of peoples
    int N = 5;
   
    // Function Call
    countWays(N);
}
}
  
// This code is contributed by sapnasingh4991

Javascript

<script>
  
// Javascript program for the above approach
  
let mod = 1000000007;
  
// Function to find 2^x using
// modular exponentiation
function exponentMod(A, B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;
  
    // If B is even
    let y;
    if (B % 2 == 0) {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }
  
    // If B is odd
    else {
        y = A % mod;
        y = (y * exponentMod(A, B - 1)
            % mod)
            % mod;
    }
  
    return ((y + mod) % mod);
}
  
// Function to count the number of
// ways to form the group having
// one leader
function countWays(N)
{
  
    // Find 2^(N-1) using modular
    // exponentiation
    let select = exponentMod(2,
                                N - 1);
  
    // Count total ways
    let ways
        = ((N % mod)
        * (select % mod));
  
    ways %= mod;
  
    // Print the total ways
    document.write(ways);
}
  
// Driver Code
  
    // Given N number of peoples
    let N = 5;
  
    // Function Call
    countWays(N);
  
// This code is contributed by Mayank Tyagi
  
</script>
Producción: 

80

Complejidad temporal: O(log N) 
Espacio auxiliar: O(1)
 

Publicación traducida automáticamente

Artículo escrito por VikasVishwakarma1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *