Recuento de triángulos equiláteros de longitud unitaria posible a partir de un hexágono dado

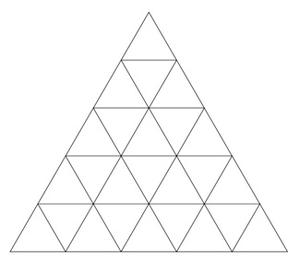
Dada una array S[] que consta de las longitudes de los 6 lados de un hexágono, la tarea es calcular el número de triángulos equiláteros de longitud unitaria que se pueden formar a partir del hexágono dado.

Ejemplos:

Entrada: S = {1, 1, 1, 1, 1, 1} 
Salida: 6 
Explicación: 
 

 

Entrada : S = {2, 2, 1, 3, 1, 2} 
Salida: 19 
Explicación: 
 

 

Enfoque: Es necesario hacer las siguientes observaciones para resolver el problema dado: 
 

• Considere un triángulo equilátero de longitud de lado ‘X’ . Se ha dividido en triángulos más pequeños de una unidad de longitud cada uno, trazando líneas paralelas a sus lados.
• A continuación se muestran las imágenes de tres de estos triángulos equiláteros: 
   

Ejemplo 1: X = 2

Ejemplo 2: X = 3

Ejemplo 3: X = 5

• En cada uno de los tres ejemplos anteriores, el recuento de triángulos equiláteros de longitud unitaria posibles es: 
   

1. X = 2: 4 triángulos equiláteros de 1 unidad de longitud de lado.
2. X = 3: 9 triángulos equiláteros de 1 unidad de longitud de lado.
3. X = 5: 25 triángulos equiláteros de 1 unidad de longitud de lado.
    

• Por observación, es claro que, para un triángulo equilátero de longitud de lado X , son posibles X ² triángulos equiláteros de longitud unitaria.
• Extendiendo esta observación a los hexágonos, inscriba hexágonos dentro de los triángulos equiláteros, como se muestra a continuación:

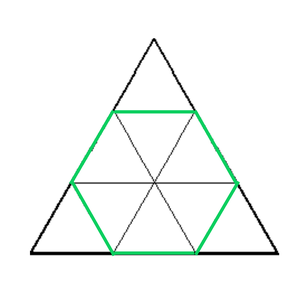
Un Hexágono regular inscrito en un triángulo equilátero de lado X = 3, tiene 6 mini triángulos en su interior.

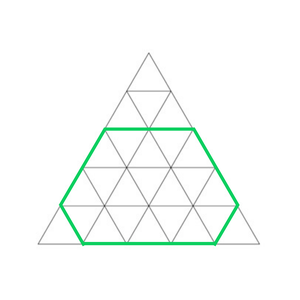
Un Hexágono irregular inscrito en el triángulo equilátero de lado X = 5, tiene 19 mini triángulos en su interior.

• Se puede observar que al quitar un cierto número de mini triángulos del triángulo más grande, se puede encontrar el hexágono con las dimensiones dadas.

La fórmula para contar el número de triángulos de unidad de longitud se puede generalizar para un hexágono que tiene seis lados S ₁ , S ₂ , S ₃ , S ₄ , S ₅ , S ₆ como:

Número de triángulos que se pueden formar = ( S ₁ + S ₂ + S ₃ ) ² – S ₁ ² – S ₃ ² – S ₅ ²

A continuación se muestra la implementación del enfoque anterior:

// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate the
// the number of Triangles possible
int calculateTriangles(int sides[])
{
    double count = pow(sides[0] + sides[1] +
                       sides[2], 2);
    count -= pow(sides[0], 2);
    count -= pow(sides[2], 2);
    count -= pow(sides[4], 2);
     
    return (int)(count);
}
 
// Driver Code
int main()
{
     
    // Regular Hexagon
    int sides[] = { 1, 1, 1, 1, 1, 1 };
    cout << (calculateTriangles(sides)) << endl;
 
    // Irregular Hexagon
    int sides1[] = { 2, 2, 1, 3, 1, 2 };
    cout << (calculateTriangles(sides1)) << endl;
     
    return 0;
}
 
// This code is contributed by 29AjayKumar

// Java program to implement
// the above approach
import java.util.*;
 
class GFG{
 
// Function to calculate the
// the number of Triangles possible
static int calculateTriangles(int sides[])
{
    double count = Math.pow(sides[0] + sides[1] +
                            sides[2], 2);
    count -= Math.pow(sides[0], 2);
    count -= Math.pow(sides[2], 2);
    count -= Math.pow(sides[4], 2);
     
    return (int)(count);
}
 
// Driver Code
public static void main(String[] args)
{
     
    // Regular Hexagon
    int sides[] = { 1, 1, 1, 1, 1, 1 };
    System.out.print((calculateTriangles(sides)) + "\n");
 
    // Irregular Hexagon
    int sides1[] = { 2, 2, 1, 3, 1, 2 };
    System.out.print((calculateTriangles(sides1)) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

# Python3 Program to implement
# the above approach
 
# Function to calculate the
# the number of Triangles possible
def calculateTriangles(sides):
    count = pow( sides[0] + sides[1] + sides[2], 2)
    count -= pow( sides[0], 2)
    count -= pow( sides[2], 2)
    count -= pow( sides[4], 2)
     
    return int(count)
 
# Driver Code
 
# Regular Hexagon
sides = [1, 1, 1, 1, 1, 1]
print(calculateTriangles(sides))
 
# Irregular Hexagon
sides = [2, 2, 1, 3, 1, 2]
print(calculateTriangles(sides))

// C# program to implement
// the above approach
using System;
 
class GFG{
 
// Function to calculate the
// the number of Triangles possible
static int calculateTriangles(int []sides)
{
    double count = Math.Pow(sides[0] + sides[1] +
                            sides[2], 2);
    count -= Math.Pow(sides[0], 2);
    count -= Math.Pow(sides[2], 2);
    count -= Math.Pow(sides[4], 2);
     
    return (int)(count);
}
 
// Driver Code
public static void Main(String[] args)
{
     
    // Regular Hexagon
    int []sides = { 1, 1, 1, 1, 1, 1 };
    Console.Write((calculateTriangles(sides)) + "\n");
 
    // Irregular Hexagon
    int []sides1 = { 2, 2, 1, 3, 1, 2 };
    Console.Write((calculateTriangles(sides1)) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

<script>
 
// JavaScript program to implement
// the above approach
 
// Function to calculate the
// the number of Triangles possible
function calculateTriangles(sides)
{
    let count = Math.pow(sides[0] + sides[1] +
                            sides[2], 2);
    count -= Math.pow(sides[0], 2);
    count -= Math.pow(sides[2], 2);
    count -= Math.pow(sides[4], 2);
       
    return (count);
}
 
// Driver Code
 
    // Regular Hexagon
    let sides = [ 1, 1, 1, 1, 1, 1 ];
    document.write((calculateTriangles(sides)) + "<br/>");
   
    // Irregular Hexagon
    let sides1 = [ 2, 2, 1, 3, 1, 2 ];
    document.write((calculateTriangles(sides1)) + "<br/>");
                 
</script>

6
19

Tiempo Complejidad: O(1)  
Espacio Auxiliar: O(1)