Es posible reducir la inferencia de primer orden a la inferencia proposicional una vez que se establecen las reglas para inferir oraciones no cuantificadas a partir de oraciones cuantificadas. El primer concepto es que, así como una instanciación puede reemplazar un enunciado existencialmente cuantificado, el conjunto de todas las instanciaciones potenciales puede reemplazar una oración universalmente cuantificada. Considere el siguiente escenario: nuestra base de conocimiento solo contiene las líneas
![]()
![]()
![]()
![]()
Luego, utilizando todas las sustituciones factibles de términos básicos del vocabulario de la base de conocimientos, en este caso, ![]() y
y ![]() , aplicamos UI a la primera frase. Obtenemos
, aplicamos UI a la primera frase. Obtenemos 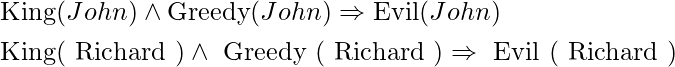
No usamos la oración universalmente cuantificada. Si las oraciones atómicas ![]() básicas, etc., se ven como símbolos de proposiciones, la base de conocimiento ahora es básicamente proposicional. Como resultado, cualquiera de los procedimientos proposicionales comprensivos puede usarse para llegar a conclusiones como
básicas, etc., se ven como símbolos de proposiciones, la base de conocimiento ahora es básicamente proposicional. Como resultado, cualquiera de los procedimientos proposicionales comprensivos puede usarse para llegar a conclusiones como ![]() .
.
La técnica de proposicionalización se puede aplicar a cualquier base de conocimiento o consulta de primer orden, preservando la vinculación. Como resultado, tenemos un método integral de decisión de vinculación… ¿o no? Hay un problema: cuando se incluye un símbolo de función en la base de conocimientos, ¡el número de posibles sustituciones de términos básicos es ilimitado! Si el ![]() símbolo se menciona en la base de conocimiento, por ejemplo, se puede crear un número ilimitado de términos anidados, como
símbolo se menciona en la base de conocimiento, por ejemplo, se puede crear un número ilimitado de términos anidados, como ![]() Con un número infinito de oraciones, nuestros algoritmos proposicionales tendrán problemas.
Con un número infinito de oraciones, nuestros algoritmos proposicionales tendrán problemas.
Afortunadamente, Jacques Herbrand (1930) demostró que si un enunciado está implícito en la base de conocimiento original de primer orden, entonces puede demostrarse utilizando solo una parte finita de la base de conocimiento proposicional. Podemos descubrir el subconjunto produciendo todas las instanciaciones con símbolos constantes ( ![]() ), luego todos los términos de profundidad 1
), luego todos los términos de profundidad 1 ![]() , luego todos los términos de profundidad 2, y así sucesivamente, hasta que podamos producir una prueba proposicional de la oración implicada.
, luego todos los términos de profundidad 2, y así sucesivamente, hasta que podamos producir una prueba proposicional de la oración implicada.
Hemos esbozado un enfoque completo para la inferencia de primer orden a través de proposicionalización, que puede probar cualquier frase implicada. Dada la gran cantidad de modelos concebibles, este es un logro significativo. Sin embargo, ¡no sabremos si la sentencia está implicada hasta que se complete la prueba! ¿Qué sucede si la oración no va seguida de una cláusula? ¿Es posible determinar esto? Resulta que no podemos para la lógica de primer orden. Nuestro procedimiento de prueba puede continuar indefinidamente, generando más y más palabras profundamente anidadas, pero no sabremos si está encerrado en un bucle sin fin o si la prueba está a punto de surgir. El problema de la detención de las máquinas de Turing es muy similar a este. Alonzo Church (1936) y Alan Turing (1936) demostraron la inevitabilidad de esta situación de manera separada. Para la lógica de primer orden,
Publicación traducida automáticamente
Artículo escrito por Mohit Gupta_OMG 🙂 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA