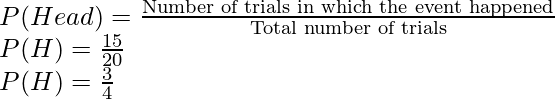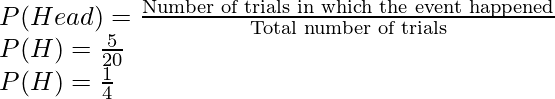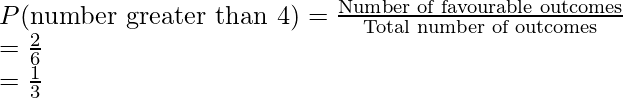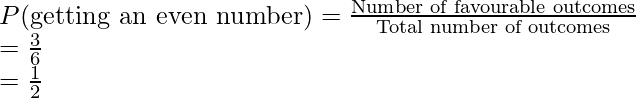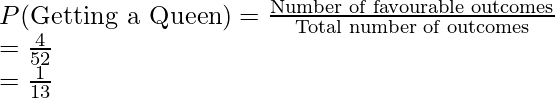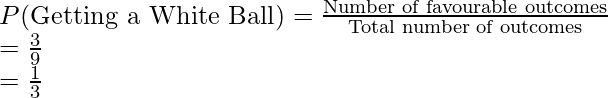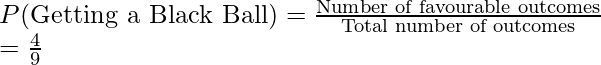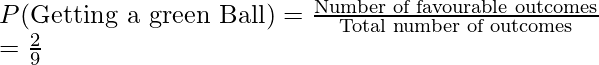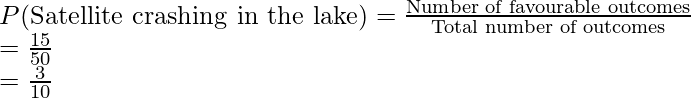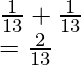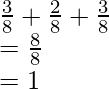Regla de adición para probabilidad

Como parte de la sociedad, la comunicación con las personas que nos rodean es muy común y no todas las comunicaciones incluyen hechos. Los hechos son la verdad universal que todos sabemos que son ciertos y existen, pero ¿qué pasa si alguien dice «Hoy puede llover»? ¿Se considera que esto es un hecho? No, porque ni es una verdad universal ni hay certeza de que ese evento ocurra.

Hay algunas declaraciones dadas en una lista a continuación, echemos un vistazo más de cerca:

India probablemente ganará hoy.
Tal vez el Primer Ministro haga un anuncio esta noche.
Puede haber algunas posibilidades de que el famoso músico John Mayer venga de gira a la India.
Hay una probabilidad de 50-50 de que el Barcelona venza al Real Madrid hoy.

Tenga en cuenta que todas estas declaraciones tienen palabras como «probablemente», «posibilidades», etc. Estas declaraciones no son ciertas, existe la posibilidad de que sucedan estas cosas, pero no es necesario que sucedan. Entonces, esta incertidumbre que está presente en estas declaraciones es capturada por la «Probabilidad» en términos matemáticos. Definamos probabilidad en términos formales.

Probabilidad

La probabilidad es un enfoque experimental del juego de posibilidades con el que nos encontramos todos los días en nuestras vidas. Es una manera de describir estas “oportunidades” de forma matemática y luego analizarlas. Nos permite medir las posibilidades de que algo ocurra.

El concepto de probabilidad fue desarrollado por el famoso filósofo y matemático Blaise Pascal en el siglo XVII.

Hagamos un experimento,

Supongamos que tenemos una moneda, la lanzamos varias veces y luego recopilamos los datos sobre caras y cruces. Realizaremos este experimento varias veces y registraremos los datos en una tabla.

Número total de veces que se lanza una moneda	Número de cabezas	Número de colas
5	2	3
10	7	3
15	9	6
20	9	11

Calculemos los valores de dos fracciones dadas a continuación,

$\frac{\text{Number of Heads}}{\text{Total number of times coin tossed}}$

Ahora bien, si seguimos calculando estos valores, notaremos que los valores comienzan a converger hacia 0,5 a medida que aumenta el número de ensayos de experimentos.

Prueba

Un ensayo es una acción que produce uno o más resultados

En el experimento dado, lanzar una moneda al aire es una prueba.

Evento

Un evento es un resultado del juicio.

Obtener cara o cruz después de lanzar la moneda puede considerarse un evento en nuestro experimento. Ahora definamos probabilidad.

Espacio muestral

Es el conjunto de todos los resultados posibles.

Dado que el espacio muestral está formado por todos los resultados posibles. En nuestro caso, el número de caras puede variar desde 0 hasta el número de veces que se lanza la moneda.

{0, 1, 2, 3, …..n}

Probabilidad

Es un valor que denota las posibilidades de ocurrencia de algún evento.

Sea “n” el número total de intentos y E un evento. La probabilidad de ocurrencia de ese evento es,

$P(E) = \frac{\text{Number of trials in which the event happened}}{\text{Total number of trials}}$

Note que por su definición, el numerador siempre será menor o igual que el denominador. Asi que,

P(E) ≤ 1

Pregunta: Con base en el experimento anterior, digamos que se lanzó una moneda 20 veces y obtuvimos 15 caras y 5 cruces. Encuentre la probabilidad de obtener cara y cruz cuando esta moneda se lanza de nuevo.

Solución:

Sabemos que la moneda se lanzó 20 veces, supongamos que queremos calcular la probabilidad de cara primero.

Probabilidad de cara:

Entonces, el evento que buscaremos es obtener cara, esto sucedió 15 veces cuando la moneda se lanzó 20 veces.

$P(Head) = \frac{\text{Number of trials in which the event happened}}{\text{Total number of trials}} \\ P(H)= \frac{15}{20} \\ P(H)= \frac{3}{4}$

Probabilidad de cruz:

Entonces, el evento que buscaremos es obtener una cara, esto sucedió 5 veces cuando la moneda se lanzó 20 veces.

$P(Head) = \frac{\text{Number of trials in which the event happened}}{\text{Total number of trials}} \\ P(H)= \frac{5}{20} \\ P(H)= \frac{1}{4}$

Observe que en el ejemplo anterior, la probabilidad de cara y la probabilidad de cruz cuando se suman, nos dan 1.

Probabilidad con Diagramas de Venn

Antes de presentar los diagramas de Venn, debemos echar un vistazo al término «mutuamente exclusivo».

Mutuamente excluyentes: Digamos que hay dos eventos A y B en un ensayo. Si ambos no pueden ocurrir simultáneamente, entonces ambos eventos son mutuamente excluyentes.

Por ejemplo: en el experimento de lanzar una moneda, no son posibles cara y cruz a la vez. Por lo tanto, son eventos mutuamente excluyentes en la naturaleza.

Otro ejemplo,

Digamos que se lanzó un dado, el evento A arroja un número impar y el evento B arroja el número 3. Ahora, cuando sale 3 de los dados, los eventos A y B ocurren simultáneamente. Por lo tanto, no son mutuamente excluyentes.

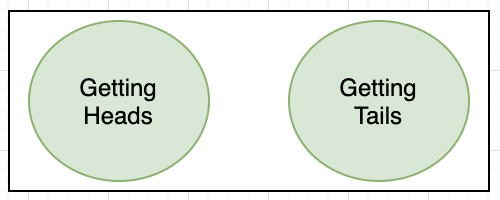
Los diagramas a continuación representan el Diagrama de Venn para el experimento de lanzamiento de moneda que hicimos anteriormente. Dado que ambos eventos son mutuamente excluyentes, estos círculos no se cruzan.

Para el ejemplo de una tirada de dado, hagamos un diagrama de Venn para el evento A y el evento B. Observe que los resultados 1, 5 y 3 están en un círculo que denota el evento A. 3 es común a ambos eventos y, por lo tanto, se encuentra en la intersección. 4 y 6 no vienen en ningún caso y, por lo tanto, se encuentran fuera del espacio muestral.

Estos eventos no son mutuamente excluyentes, por lo que los diagramas se cruzan.

Adición de probabilidades

En el primer ejemplo, vimos que la probabilidad de cara y la probabilidad de cruz sumaban 1. Esto da lugar a otra regla de probabilidad.

Para eventos mutuamente excluyentes. La Suma de todas las probabilidades de todos los eventos en un experimento es siempre 1. Por ejemplo:

Si un ensayo tiene tres resultados posibles, A, B y C.

P(A) + P(B) + P(C) = 1

A veces sólo tenemos un resultado en el que estamos interesados. Digamos que 8 equipos están participando en la Copa Mundial de Cricket. Estamos interesados en encontrar la probabilidad de que India gane la copa del mundo. No estamos interesados en averiguar la probabilidad de todos los demás equipos. Por lo que formularemos el problema de la siguiente manera,

Digamos que el evento A indica que India ganó la copa del mundo. Entonces, otro evento B denota que India no ganó la copa del mundo.

P(A) + P(B) = 1

P(A) = 1 – P(B)

Tales eventos se llaman eventos elementales.

Regla 1: Cuando los eventos son Mutuamente Exclusivos

Regla 2: Cuando los eventos no son mutuamente excluyentes

no mutuamente

Veamos algunos problemas con estos conceptos.

Problemas de muestra

Pregunta 1: Digamos que se lanzó un dado. Responde las siguientes preguntas:

¿Cuál es la probabilidad de obtener un número mayor que 4?
Cual es la probabilidad de obtener un numero par.

Solución:

Cuando se lanza un dado, hay seis resultados posibles.

1, 2, 3, 4, 5 y 6

Probabilidad de obtener un número mayor que 4:

Número de resultados favorables = 2

Número total de resultados = 6

$P(\text{number greater than 4}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{2}{6} \\ = \frac{1}{3}$

Probabilidad de obtener un número par:

Número de resultados favorables = 3

Número total de resultados = 6

$P(\text{getting an even number}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{3}{6} \\ = \frac{1}{2}$

Pregunta 2: Digamos que se extrajo una carta de un mazo de cartas bien barajado. Encuentre la probabilidad de obtener una Reina en un sorteo.

Solución:

Sabemos que una baraja tiene 52 cartas. Así que hay un total de 52 resultados que son posibles si se saca una carta. También sabemos que hay cuatro reinas en la baraja. Estos son nuestros resultados favorables.

Asi que,

Número total de resultados = 52

Número total de resultados favorables = 4

$P(\text{Getting a Queen}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{4}{52} \\ = \frac{1}{13}$

Pregunta 3: Una bolsa contiene 3 bolas blancas, 4 bolas negras y 2 bolas verdes. Se extrae una bola con reposición. Encuentre la probabilidad de obtener:

una bola blanca
una bola negra
una bola verde

Solución:

Hay un total de 3 + 4 + 2 = 9 bolas.

1. Probabilidad de sacar bola blanca

Número total de bolas = 9,

Resultados favorables = 3

$P(\text{Getting a White Ball}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{3}{9} \\ = \frac{1}{3}$

2. Probabilidad de sacar una bola negra

Número total de bolas = 9,

Resultados favorables = 4

$P(\text{Getting a Black Ball}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{4}{9}$

3. Probabilidad de sacar una bola negra

Número total de bolas = 9,

Resultados favorables = 2

$P(\text{Getting a green Ball}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{2}{9}$

Pregunta 4: Un satélite del espacio se estrelló contra la tierra. La siguiente figura indica el área en la que ISRO sospecha que se estrelló el satélite. Halla la probabilidad de que se estrelle en el lago.

Solución:

En esto no sabemos el número de resultados. Este es un caso continuo, es decir, el avión puede estrellarse en cualquier parte del área.

Entonces, área total de la región = 10 × 5 = 50 Km ²

Área total del lago = 5 × 3 = 15 Km ²

Ahora podemos usar estas áreas para calcular la probabilidad.

Número total de resultados posibles (área en este caso) = 50 Km ²

Número total de resultados favorables (área del lago en este caso) = 5 × 3 = 15 Km ²

$P(\text{Satellite crashing in the lake}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} \\ = \frac{15}{50} \\ = \frac{3}{10}$

Por lo tanto, la probabilidad de que el satélite se estrelle en el lago es de 0,3.

Pregunta 5: Digamos que tenemos un mazo bien barajado. Sacamos dos cartas, encontramos la probabilidad de obtener un Rey o una Reina.

Solución:

Digamos que dibujar un rey representa un evento A mientras que dibujar una reina representa un evento B. Se nos pide la probabilidad de obtener Rey o Reina. Usaremos la ley de la suma de probabilidades aquí,

Probabilidad (Rey o Reina) = Probabilidad (Rey) + Probabilidad (Reina)

Sabemos que hay 4 reyes y 4 reinas en la baraja.

P(Rey) = $\frac{4}{52} = \frac{1}{13}$

P(Reina) = $\frac{4}{52} = \frac{1}{13}$

De este modo,

Probabilidad (Rey o Reina) = $\frac{1}{13} + \frac{1}{13} \\ = \frac{2}{13}$

Pregunta 6: Tenemos una urna que contiene tres bolas negras, dos bolas azules y tres bolas blancas. Encuentre la probabilidad de obtener una bola negra, una azul y una blanca si sacamos tres veces con reemplazo.

Solución:

Tenemos un total de ocho bolas.

P(obtener una bola negra) = $\frac{3}{8}$

P(obtener una bola azul) = $\frac{2}{8}$

P(sacar una bola blanca) = $\frac{3}{8}$

Encontraremos esta probabilidad con la ley de la suma.

Así que la probabilidad total de obtener los tres colores = P(Negro) + P(Azul) + P(Blanco)

= $\frac{3}{8} + \frac{2}{8} + \frac{3}{8} \\ = \frac{8}{8} \\ = 1$

Observe que la probabilidad suma uno. Esto está de acuerdo con las leyes de la probabilidad.

Pregunta 7: El presupuesto de la Unión será anunciado por el gobierno esta semana. Se da la probabilidad de que se anuncie en un día,

Día	Probabilidad
Lunes	$\text{[math]}$ $\frac{1}{7}$
martes	$\text{[math]}$ $\frac{3}{7}$
miércoles	$\text{[math]}$ $\frac{1}{7}$
jueves	$\text{[math]}$ $\frac{1}{7}$
Viernes	$\text{[math]}$ $\frac{1}{7}$

Encuentre la probabilidad de que el presupuesto se anuncie entre el lunes y el miércoles.

Solución:

Necesitamos usar la ley de la suma de probabilidades,

P(lunes a miércoles) = P(lunes) + P(martes) + P(miércoles)

P(lunes) = $\frac{1}{7}$

P(martes) = $\frac{3}{7}$

P(miércoles) = $\frac{1}{7}$

P(lunes a miércoles) = P(lunes) + P(martes) + P(miércoles)

= $\frac{1}{7} + \frac{3}{7} + \frac{1}{7}$

= $\frac{5}{7}$

Pregunta 8: En una clase de 90 estudiantes, 50 tomaron Matemáticas, 25 tomaron Física, 30 tomaron Matemáticas y Física. Encuentre el número de estudiantes que han tomado Matemáticas o Física.

Solución:

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Probabilidad

Probabilidad con Diagramas de Venn

Adición de probabilidades

Problemas de muestra

Deja una respuesta Cancelar la respuesta