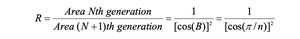Relación del área de dos polígonos anidados formados al conectar los puntos medios de los lados de un polígono regular de N lados

Dado un polígono de N lados , la tarea es encontrar la relación del área de los polígonos anidados regulares de N ^-th a (N + 1) ^N – th generados al unir los puntos medios de los lados del polígono original.

Ejemplos:

Entrada: N = 3
Salida: 4.000000
Explicación:

Triángulo anidado

La razón de la longitud de los lados formados al unir los puntos medios del triángulo con la longitud del lado del triángulo original es 0,5. Por lo tanto, R = (Área de N- ^ésimo triángulo) / (Área de (N + 1) ^-ésimo triángulo) = 4

Entrada: N = 4
Salida: 2.000000

Enfoque: El problema se puede resolver con base en las siguientes observaciones:

• Considere un polígono regular de N lados como se muestra en la siguiente figura.

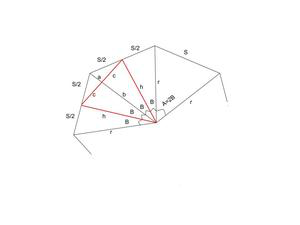
Representación de polígono regular anidado de N lados.

• A = 2 * ℼ / N 
  B = ℼ / N 
  h = r * cos(B) 
  b = h * cos(B) 
  c = h((1 – cos(A)) / 2) ^1/2
• Área del Triángulo Isósceles Negro :

• Área del Triángulo Isósceles Rojo:

• r = s / (2 * [1 – cos(2B)]) ^1/2 y b = r * [cos(B)] ²
• Después de combinar las ecuaciones anteriores:

• El resultado final obtenido es el siguiente:

A continuación se muestra la implementación del enfoque anterior:

// C++ code for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
void AreaFactor(int n)
{
    // Stores the value of PI
    double pi = 3.14159265;
 
    // Calculating area the factor
    double areaf = 1 / (cos(pi / n)
                        * cos(pi / n));
 
    // Printing the ratio
    // precise upto 6 decimal places
    cout << fixed << setprecision(6)
         << areaf << endl;
}
 
// Driver Code
int main()
{
    int n = 4;
    AreaFactor(n);
 
    return 0;
}

// Java program for the above approach
import java.io.*;
 
class GFG{
 
// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
static void AreaFactor(int n)
{
     
    // Stores the value of PI
    double pi = 3.14159265;
  
    // Calculating area the factor
    double areaf = 1 / (Math.cos(pi / n) *
                        Math.cos(pi / n));
  
    // Printing the ratio
    // precise upto 6 decimal places
    System.out.format("%.6f", areaf);
}
 
// Driver Code
public static void main(String[] args)
{
    int n = 4;
     
    AreaFactor(n);
}
}
 
// This code is contributed by code_hunt

# Python3 code for the above approach
import math
 
# Function to calculate the ratio of
# area of N-th and (N + 1)-th nested
# polygons formed by connecting midpoints
def AreaFactor(n):
 
    # Stores the value of PI
    pi = 3.14159265
 
    # Calculating area the factor
    areaf = 1 / (math.cos(pi / n) *
                 math.cos(pi / n))
 
    # Printing the ratio
    # precise upto 6 decimal places
    print('%.6f' % areaf)
     
# Driver Code
if __name__ == "__main__":
   
    n = 4
    AreaFactor(n)
 
# This code is contributed by ukasp

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG {
 
// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
static void AreaFactor(int n)
{
      
    // Stores the value of PI
    double pi = 3.14159265;
   
    // Calculating area the factor
    double areaf = 1 / (Math.Cos(pi / n) *
                        Math.Cos(pi / n));
   
    // Printing the ratio
    // precise upto 6 decimal places
    Console.WriteLine(Math.Round(areaf));
 
}
    // Driver Code
    public static void Main(string[] args)
    {
        int n = 4;
      
        AreaFactor(n);
    }
}
 
// This code is contributed by susmitakundugoaldanga.

<script>
 
// Javascript program implementation
// of the approach
 
// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
function AreaFactor(n)
{
    // Stores the value of PI
    let pi = 3.14159265;
  
    // Calculating area the factor
    let areaf = (1 / (Math.cos(pi / n)
                        * Math.cos(pi / n)));
  
    // Printing the ratio
    // precise upto 6 decimal places
    document.write(areaf.toFixed(6));
}
 
// Driver Code
     
        let n = 4;
    AreaFactor(n);
 
// This code is contributed by splevel62.
</script>

2.000000

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)