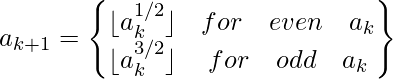Juggler Sequence es una serie de números enteros en los que el primer término comienza con un número entero positivo a y los términos restantes se generan a partir del término inmediatamente anterior utilizando la siguiente relación de recurrencia:
Secuencia de malabaristas que comienza con el número 3:
5, 11, 36, 6, 2, 1
Secuencia de malabaristas que comienza con el número 9:
9, 27, 140, 11, 36, 6, 2, 1
Dado un número N , tenemos que imprimir la Sucesión malabarista para este número como el primer término de la sucesión.
Ejemplos :
Entrada: N = 9
Salida: 9, 27, 140, 11, 36, 6, 2, 1
Comenzamos con 9 y usamos la fórmula anterior para obtener los siguientes términos.Entrada: N = 6
Salida: 6, 2, 1
Enfoque iterativo: Ya hemos visto el enfoque iterativo en el Conjunto 1 de este problema.
Enfoque recursivo: en este enfoque, recorreremos recursivamente comenzando desde N. Siga los pasos a continuación para cada paso recursivo
- Salida del valor de N
- Si N ha llegado a 1 finaliza la recursividad
- De lo contrario, siga la fórmula basada en que el número sea impar o par y llame a la función recursiva en el número recién derivado.
A continuación se muestra la implementación del enfoque:
C++
// C++ code for the above approach
#include <bits/stdc++.h>
using namespace std;
// Recursive function to print
// the juggler sequence
void jum_sequence(int N)
{
cout << N << " ";
if (N <= 1)
return;
else if (N % 2 == 0)
{
N = floor(sqrt(N));
jum_sequence(N);
}
else
{
N = floor(N * sqrt(N));
jum_sequence(N);
}
}
// Driver code
int main()
{
// Juggler sequence starting with 10
jum_sequence(10);
return 0;
}
// This code is contributed by Potta Lokesh
Java
// Java code for the above approach
class GFG
{
// Recursive function to print
// the juggler sequence
public static void jum_sequence(int N) {
System.out.print(N + " ");
if (N <= 1)
return;
else if (N % 2 == 0) {
N = (int) (Math.floor(Math.sqrt(N)));
jum_sequence(N);
} else {
N = (int) Math.floor(N * Math.sqrt(N));
jum_sequence(N);
}
}
// Driver code
public static void main(String args[]) {
// Juggler sequence starting with 10
jum_sequence(10);
}
}
// This code is contributed by Saurabh Jaiswal
Python3
# Python code to implement the above approach # Recursive function to print # the juggler sequence def jum_sequence(N): print(N, end =" ") if (N == 1): return elif N & 1 == 0: N = int(pow(N, 0.5)) jum_sequence(N) else: N = int(pow(N, 1.5)) jum_sequence(N) # Juggler sequence starting with 10 jum_sequence(10)
C#
// C# code for the above approach
using System;
class GFG{
// Recursive function to print
// the juggler sequence
public static void jum_sequence(int N)
{
Console.Write(N + " ");
if (N <= 1)
return;
else if (N % 2 == 0)
{
N = (int)(Math.Floor(Math.Sqrt(N)));
jum_sequence(N);
}
else
{
N = (int)Math.Floor(N * Math.Sqrt(N));
jum_sequence(N);
}
}
// Driver code
public static void Main()
{
// Juggler sequence starting with 10
jum_sequence(10);
}
}
// This code is contributed by Saurabh Jaiswal
Javascript
<script>
// Javascript code for the above approach
// Recursive function to print
// the juggler sequence
function jum_sequence(N){
document.write(N +" ");
if (N <= 1)
return;
else if (N % 2 == 0)
{
N = Math.floor(Math.sqrt(N));
jum_sequence(N);
}
else
{
N = Math.floor(N * Math.sqrt(N));
jum_sequence(N);
}
}
// Driver code
// Juggler sequence starting with 10
jum_sequence(10);
// This code is contributed by gfgking
</script>
10 3 5 11 36 6 2 1
Complejidad temporal: O(N)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por akshaypathak3334444 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA