Clase 10 Soluciones NCERT – Capítulo 1 Números reales – Ejercicio 1.4

Teorema 1.5 de NCERT: Sea x un número racional cuya expansión decimal termina. Entonces x se puede expresar en la forma, $\frac{p}{q}$ donde p y q son coprimos, y la descomposición en factores primos de q es de la forma 2 ⁿ 5 ^m , donde n, m son números enteros no negativos.

Teorema 1.6 del NCERT: Sea x = $\frac{p}{q}$ un número racional, tal que la descomposición en factores primos de q sea de la forma 2 ⁿ 5 ^m , donde n, m son números enteros no negativos. Entonces x tiene una expansión decimal que termina.

Pregunta 1. Sin realizar realmente la división larga, indique si los siguientes números racionales tendrán una expansión decimal terminal o una expansión decimal periódica no terminal:

(i) 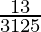$\frac{13}{3125}$

(ii) 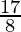$\frac{17}{8}$

(iii) 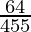$\frac{64}{455}$

(iv) 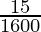$\frac{15}{1600}$

(v) 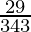$\frac{29}{343}$

(vi) 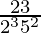$\frac{23}{2^35^2}$

(vii) 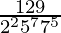$\frac{129}{2^25^77^5}$

(viii) 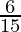$\frac{6}{15}$

(ix) 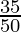$\frac{35}{50}$

(X) 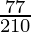$\frac{77}{210}$

Solución:

(i) $\frac{13}{3125}$

Haciendo factorización prima del denominador, obtenemos

3125 = 5×5×5 = 5 ³

Como denominador tiene la forma 2 ⁿ 5 ^m solo donde n=0 ym=3.

De acuerdo con el Teorema 1.6 ,

$\frac{13}{3125}$ tendrá una expansión decimal terminal .

(ii) $\frac{17}{8}$

Haciendo factorización prima del denominador, obtenemos

8 = 2×2×2 = 2 ³

Como denominador tiene la forma 2 ⁿ 5 ^m solo donde n=3 ym=0.

De acuerdo con el Teorema 1.6 ,

$\frac{17}{8}$ tendrá una expansión decimal terminal .

(iii) $\frac{64}{455}$

Haciendo factorización prima del denominador, obtenemos

455 = 5×7×13

Como denominador no está en la forma 2 ⁿ 5 ^m solamente.

De acuerdo con la contradicción del Teorema 1.6 ,

$\frac{64}{455}$ tendrá una expansión decimal no terminante .

(iv) $\frac{15}{1600}$

Haciendo factorización prima del denominador, obtenemos

1600 = 2×2×2×2×2×2×5×5 = 2 ⁶ 5 ²

Como denominador tiene la forma 2 ⁿ 5 ^m solo donde n=6 ym=2.

De acuerdo con el Teorema 1.6 , 1

$\frac{15}{1600}$ tendrá una expansión decimal terminal .

(v) $\frac{29}{343}$

Haciendo factorización prima del denominador, obtenemos

343 = 7×7×7 = 7 ³

Como denominador no está en la forma 2 ⁿ 5 ^m solamente.

De acuerdo con la contradicción del Teorema 1.6,

$\frac{29}{343}$ tendrá una expansión decimal no terminante .

(vi) $\frac{23}{2^35^2}$

Factorización prima del denominador, tenemos

= 2 ³ 5 ²

Como denominador tiene la forma 2 ⁿ 5 ^m solo donde n=3 y m=2.

De acuerdo con el Teorema 1.6,

$\frac{23}{2^35^2}$ tendrá una expansión decimal terminal .

(vii) $\frac{129}{2^25^77^5}$

Factorización prima del denominador, tenemos

= 2 ² 5 ⁷ 7 ⁵

Como denominador no está en la forma 2 ⁿ 5 ^m solamente.

De acuerdo con la contradicción del Teorema 1.6,

$\frac{129}{2^25^77^5}$ tendrá una expansión decimal no terminante .

(viii) $\frac{6}{15}$

$\frac{6}{15} = \frac{3}{5}$

al hacer la descomposición en factores primos del denominador, obtenemos

5 = 5 ¹

Como denominador tiene la forma 2 ⁿ 5 ^m solo donde n=0 ym=1.

De acuerdo con el Teorema 1.6 ,

$\frac{6}{15}$ tendrá una expansión decimal terminal .

(ix) $\frac{35}{50}$

al hacer la descomposición en factores primos del denominador, obtenemos

50= 2×5×5 = 2 ¹ 5 ²

Como denominador tiene la forma 2 ⁿ 5 ^m donde n=1 ym=2.

De acuerdo con el Teorema 1.6,

$\frac{35}{50}$ tendrá una expansión decimal terminal .

(X) $\frac{77}{210}$

al hacer la descomposición en factores primos del denominador, obtenemos

210 = 2×3×5×7

Como denominador no está en la forma 2 ⁿ 5 ^m solamente.

De acuerdo con la contradicción del Teorema 1.6,

$\frac{77}{210}$ tendrá una expansión decimal no terminante .

Pregunta 2. Escriba las expansiones decimales de los números racionales de la Pregunta 1 anterior que tienen expansiones decimales terminales.

(i) 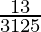$\frac{13}{3125}$

(ii) 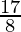$\frac{17}{8}$

(iv) 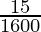$\frac{15}{1600}$

(vi) 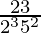$\frac{23}{2^35^2}$

(viii) 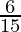$\frac{6}{15}$

(ix) 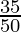$\frac{35}{50}$

Solución:

(i) $\frac{13}{3125}$

= 0.00416

(ii) $\frac{17}{8}$

= 2.125

(iv) $\frac{15}{1600}$

= 0.009375

(vi) $\frac{23}{2^35^2}$

= 0.0115

(viii) $\frac{6}{15}$

= 0,4

(ix) $\frac{35}{50}$

= 0,7

Pregunta 3. Los siguientes números reales tienen expansiones decimales como se indica a continuación. En cada caso, decide si son racionales o no. Si son racionales y de la forma, 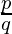$\frac{p}{q}$ ¿qué puedes decir de los factores primos de q?

(yo) 43.123456789

(ii) 0.120120012000120000. . .

(iii) 43.123456789

Solución:

(yo) 43.123456789

Como este es un número racional cuya expansión decimal termina . Entonces se puede expresar en la forma, $\frac{p}{q}$ donde p y q son coprimos, y la descomposición en factores primos de q es de la forma 2 ⁿ 5 ^m , donde n, m son números enteros no negativos.

= 43123456789 / 10 ⁹

= 43123456789 / 2 ⁹ × 5 ⁹

(ii) 0.120120012000120000…………..

Como la expansión de números decimales dados no termina ni se repite , entonces no es un número racional. Entonces no se puede expresar en la forma, $\frac{p}{q}$ donde p y q son coprimos, y la descomposición en factores primos de q es de la forma 2 ⁿ 5 ^m , donde n, m son números enteros no negativos.

(iii) 43. $\overline{123456789}$ [Tex] [/Tex]

Como la expansión del número decimal dado no termina y se repite , entonces es un número racional. Entonces se puede expresar en la forma, $\frac{p}{q}$ donde p y q son coprimos, pero la descomposición en factores primos de q no tiene la forma de 2 ⁿ 5 ^m solamente, donde n, m son números enteros no negativos

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Sin realizar realmente la división larga, indique si los siguientes números racionales tendrán una expansión decimal terminal o una expansión decimal periódica no terminal:

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii)

(ix)

(X)

Pregunta 2. Escriba las expansiones decimales de los números racionales de la Pregunta 1 anterior que tienen expansiones decimales terminales.

(i)

(ii)

(iv)

(vi)

(viii)

(ix)

Pregunta 3. Los siguientes números reales tienen expansiones decimales como se indica a continuación. En cada caso, decide si son racionales o no. Si son racionales y de la forma, ¿qué puedes decir de los factores primos de q?

Deja una respuesta Cancelar la respuesta

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iii) $\frac{64}{455}$

(iv) $\frac{15}{1600}$

(v) $\frac{29}{343}$

(vi) $\frac{23}{2^35^2}$

(vii) $\frac{129}{2^25^77^5}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

(X) $\frac{77}{210}$

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iv) $\frac{15}{1600}$

(vi) $\frac{23}{2^35^2}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

Pregunta 3. Los siguientes números reales tienen expansiones decimales como se indica a continuación. En cada caso, decide si son racionales o no. Si son racionales y de la forma, $\frac{p}{q}$ ¿qué puedes decir de los factores primos de q?