Pregunta 1. ¿Cuántas tangentes puede tener un círculo?
Solución:
Un círculo puede tener un número infinito de tangentes porque tiene un número infinito de puntos en su circunferencia y cada punto puede tener su tangente individual.
Pregunta 2. Complete los espacios en blanco:
(i) Una tangente a un círculo lo corta en _______ punto(s).
(ii) Una línea que corta un círculo en dos puntos se llama __________.
(iii) Un círculo puede tener __________ tangentes paralelas como máximo.
(iv) El punto común de una tangente a un círculo y el círculo se llama ____.
Solución:
(yo) uno
(ii) secante
(iii) dos
(iv) Punto de contacto
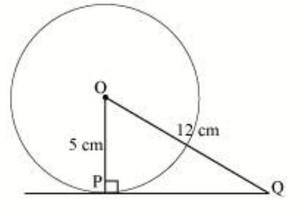
Pregunta 3. Una tangente PQ en un punto P de un círculo de 5 cm de radio corta una línea que pasa por el centro O en un punto Q de modo que OQ = 12 cm. Longitud PQ es:
A) 12 cm (B) 13 cm (C) 8,5 cm (D) √119 cm
Solución:
Como sabemos que la recta trazada desde el centro de la circunferencia hasta la tangente es perpendicular a la tangente en el punto de contacto.
Aquí OP es perpendicular a PQ.
Por lo tanto, el triángulo OPQ es un triángulo rectángulo, y podemos aplicarle el teorema de Pitágoras.
PQ = √
PQ = √(12 2 – 5 2 )cm
PQ = √119 cm
Por lo tanto, la opción D es la respuesta correcta.
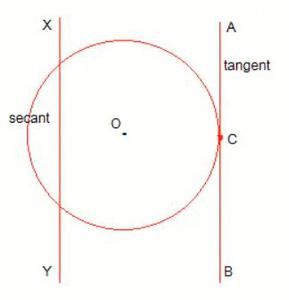
Cuestión 4. Dibujar un círculo y dos rectas paralelas a una recta dada tal que una sea tangente y la otra secante al círculo.
Solución:
Aquí AB es la tangente al círculo en el punto C y XY es la secante al círculo. Además, ambas rectas son paralelas.
Publicación traducida automáticamente
Artículo escrito por its_just_me y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA