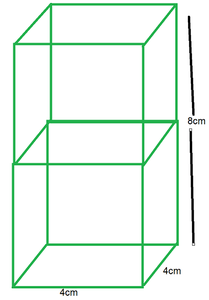
Pregunta 1. 2 cubos de 64 cm 3 de volumen cada uno están unidos por los extremos. Encuentre el área de la superficie del cuboide resultante.
Solución:
Volumen del cubo=64cm 3 = (lado) 3
(Lado) 3 = 64
Lado = (64cm 3 ) 1/3
= (2*2*2*2*2*2 cm3 ) 1/3
= 2*2
= 4 centímetros
Por lo tanto, ahora
Longitud = 8cm
ancho = 4cm
Altura = 4cm
Área de superficie del cuboide=2(lb+bh+hl)
=2(8*4+4*4+4*8)
=2(32+16+32)
=2(80)
= 160 cm 2
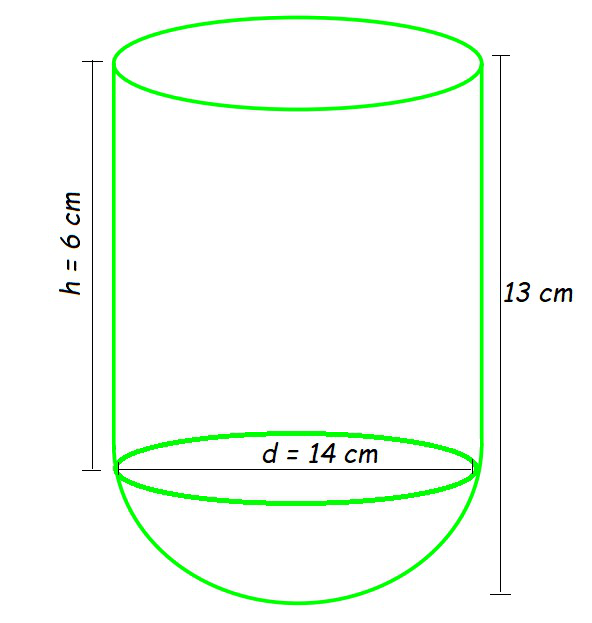
Pregunta 2. Un recipiente tiene la forma de un hemisferio hueco montado por un cilindro hueco. El diámetro de la semiesfera es de 14 cm y la altura total del recipiente es de 13 cm. Encuentre el área de la superficie interna del recipiente.
Solución:
Altura del cilindro = 13-7 = 6 cm
Área de la superficie interna de los vasos = CSA del cilindro + CSA del hemisferio
=2πrh+2πr 2
=2πr(h+r)
=2*22/7*7(6+7)
=44(13)
=572cm 2
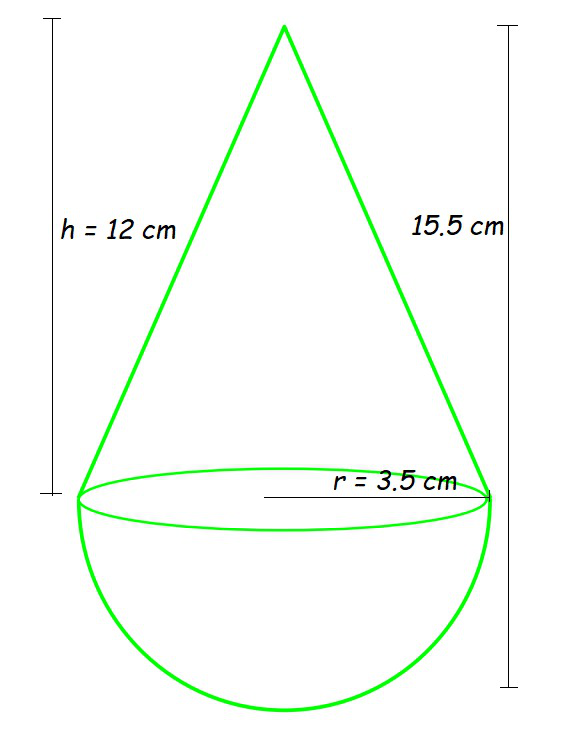
Pregunta 3. Un juguete tiene la forma de un cono de 3,5 cm de radio montado en un hemisferio del mismo radio. La altura total del juguete es de 15,5 cm. Encuentra el área total de la superficie del juguete.
Solución:
Altura del cono (h) = 15,5-3 = 12 cm
l=√(h 2 + r 2 )
l=√(12 2 +3.5 2 )
l=√(144+12.25)
=√256.25
= 12,5 cm
Superficie total del juguete = CS A del cono + CSA del hemisferio
=πrl+2πr 2
=πr(l+2r)
=22/7*3,5(12,5+2(3,5))
=11(12.5*7)
=11(19.5)
= 214,5 cm 2
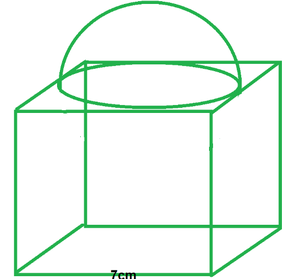
Pregunta 4. Un bloque cúbico de lado 7 cm está coronado por un hemisferio. ¿Cuál es el diámetro máximo que puede tener la semiesfera? Encuentre el área de la superficie del sólido.
Solución:
Área de superficie de sólido = TSA de cubo-Área de círculo + CSA de hemisferio
=6*lado*lado-πr 2 +2πr 2
=6*lado*lado+πr 2
=6*7*7+22/7*7/2*7/2
=294+72/2
=294+38.5
= 332,5 cm 2
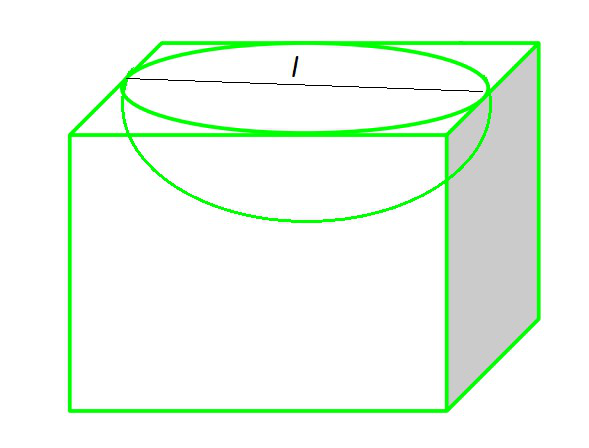
Pregunta 5. Se corta una depresión hemisférica de una cara de un bloque de madera cúbico de modo que el diámetro l del hemisferio sea igual al borde del cubo. Determine el área superficial del sólido restante.
Solución:
Área de superficie sólida = TSA del cubo -Área del círculo + CSA del hemisferio
=6*lado*lado- πr 2 +2πr 2
=6*l*l-πr 2
=6l 2 -πr 2
=6l 2 – π(l/2) 2
=6l 2 – πl 2 /4
=(24l 2 + πl 2 )/4
=l 2 (24+π)/4
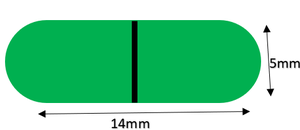
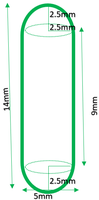
Pregunta 6. Una cápsula de medicamento tiene forma de cilindro con dos hemisferios pegados a cada uno de sus extremos. La longitud de toda la cápsula es de 14 mm y el diámetro de la cápsula es de 5 mm. Encuentre su área de superficie.
Solución:
D=5mm R=5/2mm
h=14-5=9
Área de superficie del cilindro = CS A del cilindro + CSA de 2 Hemisferio
=2πrh+2πr 2 *2
=2πr(h+2r)
=2*22/7*5/2(9+2*5/2)
=110/7(9+5)
=110/7*14
= 220 mm 2
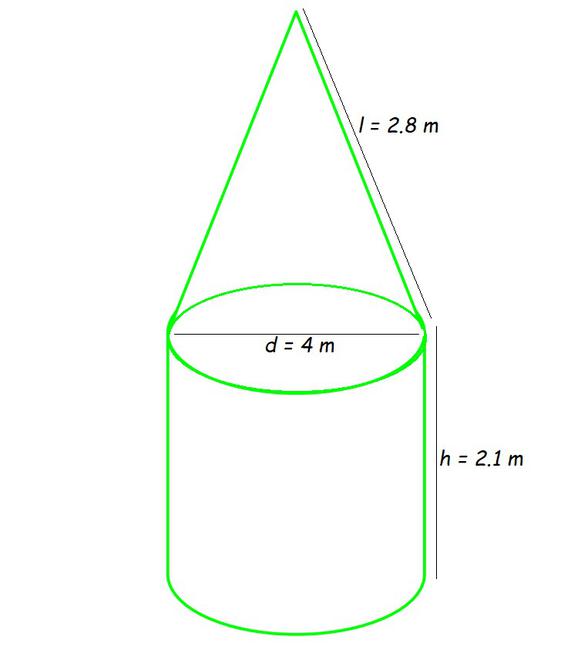
Pregunta 7. Una tienda de campaña tiene la forma de un cilindro coronado por una parte superior cónica. Si la altura y el diámetro de la parte cilíndrica son 2,1 m y 4 m respectivamente, y la altura inclinada de la parte superior es 2,8 m, encuentre el área de la lona utilizada para hacer la tienda. Además, encuentre el costo de la lona de la tienda a razón de Rs 500 por m 2 . (Tenga en cuenta que la base de la tienda no se cubrirá con lona).
Solución:
yo) d=4m r=4/2=2m
Área del lienzo =CSA del cono+ CSA del cilindro
=πrl+2πrh
=πr(l+2h)
=22/7(2.8+2*2.1)
=44*(2.8+4.2)/7
=44*7/7
=44m 2
ii) costo del lienzo=Área*tarifa
=44m 2 *Rs. 500/m 2
=$22,000
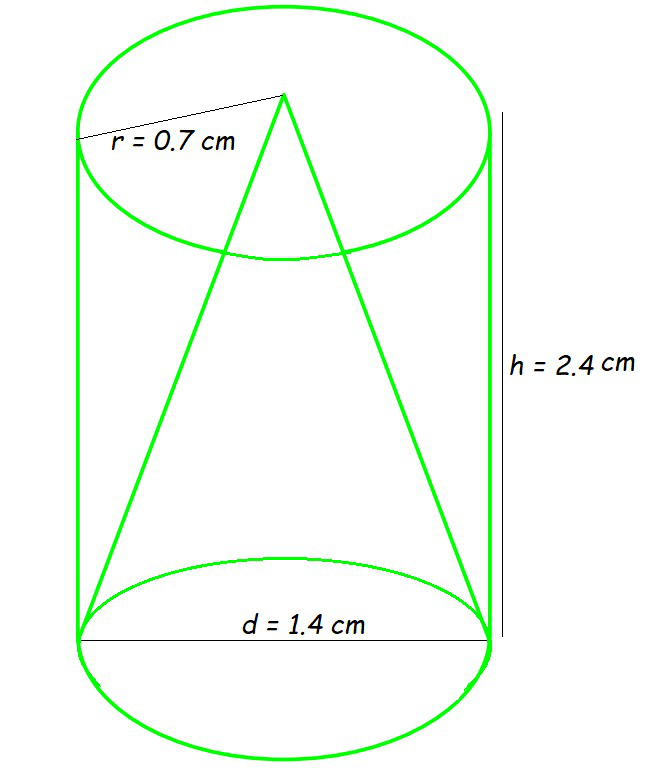
Pregunta 8. A partir de un cilindro macizo de 2,4 cm de altura y 1,4 cm de diámetro, se ahueca una cavidad cónica de la misma altura y del mismo diámetro. Encuentre el área de superficie total del sólido restante al cm 2 más cercano .
Solución:
D=1,4 cm, r=1,4/2=14/20=7/10=0,7
l= √(h 2 +r 2 )
= √((2.4) 2 +(0.7) 2 )
= √(5,76+0,49)
= √6.25
= 2,5 cm 2
Área de superficie total del sólido restante = CSA del cilindro + CSA del cono + Área de la base circular
= 2πrh+πrl+πr 2
= πr(2h+l+r)
= 22/7*7/10(2(2.4)+2.5+0.7)
= 22(4,8+2,5+0,7)/10
= 22(8)/10
= 176/10
= 17,6 cm 2
Diez más cercano = 18 cm 2
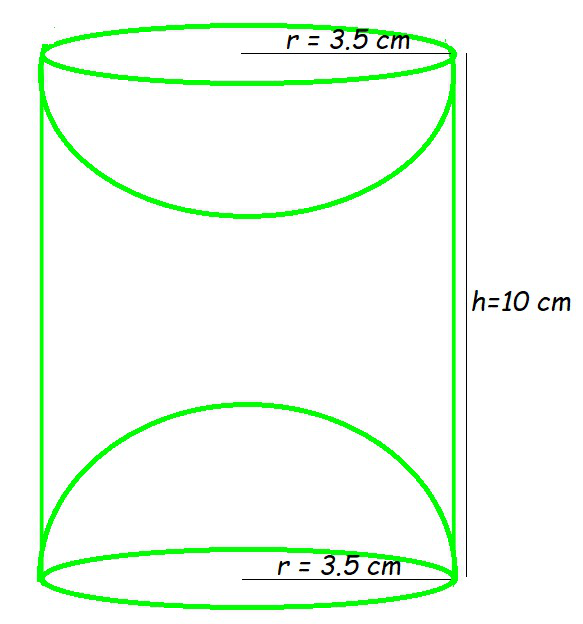
Pregunta 9. Se hizo un artículo de madera sacando una semiesfera de cada extremo de un cilindro sólido, como se muestra en la figura. Si la altura del cilindro es de 10 cm y su base tiene un radio de 3,5 cm, encuentre el área total de la superficie del artículo.
Solución:
Superficie total del artículo=CSA del cilindro+2*CSA del hemisferio
=2πrh+2*2πr 2
=2πr(h+2r)
=2*22/7*3,5(10+2(3,5))
=22(10+7)
=22(17)
=374cm 2
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA